Suhdelaskennan perusteet
1. Platonin luolavertaus tänään.
2. Suhdelaskennan alku.
3. Suhdelaskentamenettely.
4. Suhteellisuus yleisesti.
5. Suhdelaskennan etuja
6. Suhdelaskemisen suureet
7. Newtonin kokeellinen filosofia
8. Diofantoksen muistokirjoitus
9. Arvojen syntyminen
10. Kultainen leikkaus 1,618 laskenta
11. Numerot vastaan suhdelaskenta
........................
21. Viisi ensimmäistä suhdelaskennan kerrointa
22. Fibonaccin lukujono
23. Pascalin kolmio
23.1 Pascalin kolmion alin rivi
24. Nollan historia
25. Numero viisi suhdelaskennassa
26. Viisi peruslaskutapaa
27. Viisi tapaa käsitellä muutosta.
28. Samaa tarkoittava suhdelaskenta
29. Suhdelaskenta ja näkemisen geometria
30. Suhteellisuuden syntyminen
........................
41. Kemiallisten aineiden jaksollinen järjestelmä
42. Kaikella on sijainti
43. Suhdelukujono
44. Suhdelukujen yhteen- ja kertolasku
45. Eri mittayksiköt.
46. Suhteellisuuden kuvaaminen kuvioiden kautta
47. Matemaattinen olio
48. Domino vaikutus
49. Pascalin kolmion kerroin 11.
50. Eksponentiaalinen arvokäyrä
...........................
61. Kultainen leikkaus
62. Kultainen leikkaus tänään
63. Kultainen leikkaus kirjallisuudessa
64. Paperin taittaminen viisi kertaa
65. Kilometrin ja mailin suhde
66. Eri mittayksiköt
67. Elävän ja kuolleen aineen suhdeluvut
68. Havainnot
68.1 Havainto I.
68.2 Havainto II.
68.3 Havainto III.
68.4 Havainto IV.
68.5 Havainto V
68.6 Havainto VI
69. Mitat -suhde 1,618
1. Platonin luolavertaus tänään
Varjojen muodostama todellisuus liittyy näkemisen geometriaan. Valo liittyy varjoon, joka muodostaa tumman alueen valaistun materian pinnalle. Kaikki varjot eivät ole tätä, sillä esimerkiksi taipuma ja väsyminen ovat varjoja tapahtumista ja laskettavaa. Tämä tarkoittaa, että suhdelaskenta määrittää tapaukset varjojen avulla. Tämä on yksinkertaista, vaatien ainoastaan kyvyn vastaanottaa tietoa toisesta näkökulmasta. Lopulta laskenta päättyy samaan tai siihen ei pääse tunnetusti muulla tavalla. Joissakin tapauksissa minuuttien laskentaan paperilla on tarvittu vuosien kokemus lasketusta asiasta. Joitakin asioita, ette kykene koskaan laskemaan muulla tavalla.
 Me olemme Platonin esimerkin mukaisesti kaavojen kahleisiin sidottuja vankeja, jolloin tiedeuskon nimissä maailmankuva selittyy kaavoina. Tässä uskossa kysymme kaavaa millä jokin lasketaan. Päämme ovat kahleilla sidottu kaavoihin, jotka ovat myös varjoja tapahtumista. Kaavan tarkkuus on kuin nuotion valo Platonin luolaesimerkissä. Ilman kirkasta nuotion valoa, ei ole varjokuvaa, kuvausta ilmiöstä. Entä, kun kaavaa ei ole? Me olemme Platonin esimerkin mukaisesti kaavojen kahleisiin sidottuja vankeja, jolloin tiedeuskon nimissä maailmankuva selittyy kaavoina. Tässä uskossa kysymme kaavaa millä jokin lasketaan. Päämme ovat kahleilla sidottu kaavoihin, jotka ovat myös varjoja tapahtumista. Kaavan tarkkuus on kuin nuotion valo Platonin luolaesimerkissä. Ilman kirkasta nuotion valoa, ei ole varjokuvaa, kuvausta ilmiöstä. Entä, kun kaavaa ei ole?
Suhdelaskennassa, ei ole kaavatyrmään teljettyjä vankeja. Tutustumme valoon ja varjoon, valitsemalla parhaan tavan laskea kaavalla tai ilman. Kaavat ovat hyviä, mutta niiden varaan ei voi pelkästään jäädä. Jotta pystyy laskemaan tekniikkaan ja fysiikkaan liittyviä tehtäviä, on tunnettava painovoimakentän kiihtyvyys, mutta gravitaatio on huonommin tunnettu.
Gravitaatio varjon muodostaja
Kiihtyvyyden arvo painovoiman seurauksena, ei anna tuntemusta aiheesta. Käytämme esimerkiksi kerrointa 9,81 m/s2, tietämättä miksi. Oletan, ettei 99,99 % ihmisistä kykene määrittämään gravitaatiovakion Y = 6,67 x 10-11 Newton metri2/kilogramma2 muodostumista. Näin ollessa, laskenta ei perustu henkilökohtaiseen tietämiseen perusteltavalla tavalla. Laskemme gravitaation lukuisalla tavalla tunnettuun nähden. Ilman gravitaatiota, ei tarvita laskukaavoja. Mikään ei taivu, pysäytä liikettä tai pysy koossa. Tämän oivaltamalla, gravitaatio pitää kaiken koossa, pysäyttää liikkeen, taivuttaa ja väsyttää, mutta on laskettavissa. Gravitaatio muodostaa varjon, jota laskemme sen eri muodoissa.
Suhdelaskentana voi laskea tunnettua, jopa aiemmin laskemattomia asioita. Varjo käsitteenä tuo esiin asioita, jotka kirkkaassa valossa peittyvät näkymättömiksi. Vastaavaa tapahtuu mustavalkoisessa valokuvassa, jolloin aluksi tummasta kohdasta kuvaa ei pysty erottamaan yksityiskohtia. Valokuvaa kehittäessä, on mahdollista valottaa tummia kohtia enemmän ja näin saada yksityiskohdat esiin. Alivalottuneella tummalla negatiivilla tämä on mahdollista. Ylivalottunut negativi on lähes valkoinen, jolloin se on kuin tarkastelisi asioita leipäpussin läpi. Tiedän tämän, sillä minulla oli aikanaan välineistö musta-valko valokuvien valmistamiseksi. Ajatus luonnon tuntemisesta kaavoina, on ajatuksena kuollut ja johtanut kapeaan näkemykseen.
Muut laskentamenettelyt eivät ole yhtenäinen laskentamenettely. Tästä syystä sivuilla vierailun voi aloittaa haluamastaan kohdasta, tämän sotkematta kokonaiskuvaa. Rakentaminen on eräs laskennan teemoista. Avatessanne sivut, ne ovat muuttuneet. Näin ollen, ne tarkentuvat, mutta emme milloinkaa saa niitä valmiiksi. Varjojen kautta avautuu uusi maailma.
2. Suhdelaskennan alku
Minä matkustin vuonna 1983 Länsi-Saksaan ja ostin ensimmäisen tietokoneeni. Tähän pieneen laskinta muistuttavaan laitteeseen liittyi nauha-asema ja tulostin. Tällä suunnittelin tuotesarjoja, sillä yhdistettyjen ohjelmien avulla pystyi mitoittamaan sarjan tuotteita.

Noihin aikoihin määritin painot piirustuksiin suurella tarkkuudella. Myöhemmin erään yrityksen tuotantoinsinööri kiinnostui painojen määrityksestäni. Hän kertoi tarkistaneensa erään suuren tuotteen osia ja päässeen 100 gramman tarkkuudella samaan tulokseen. Edellinen perustuu kertojan ilmoittamaan tarkkuudestani. Nauhalle tulostetut laskelmat eivät olleet näyttäviä näköisiä, mutta tekivät minuun suuren vaikutuksen kolmekymmentä vuotta sitten. Samalla kiinnostuin tietämään edeltä käsin lujuuden laskennan arvoista, jotka perustuisivat tunnettuun tietoon olemassa olevasta. Tuolloin en kyennyt löytämään vastausta tähän kysymykseen. Meni 12 vuotta, kun osallistuin tähän ajatukseen perustuvalla ohjelmalla erääseen ideakilpailuun. (883)
3. Suhdelaskentamenettely
Suhdelaskenta käsittelee suhteellisuutta ja sillä on yhteys joukko-oppiin. Moni ei ole tutustunut joukko-oppiin, vaikka kaiken matematiikassa sanotaan perustuvan siihen. Joukko-oppi on käänteistiedon matemaattinen perusta, jossa tieto haetaan muun tunnetun tiedon antamalla informaatiolla. Moni silti hallitsee matemaattisen menettelyn tiedon hakemiseksi, jossa käänteisellä tiedolla saadaan kuva haettavasta, mutta ei tarkkaa arvoa. Esimerkki tästä on kirjastojen tiedon hakumenettely.

Laskelmat ovat matemaattisia tiiliä rakennelmaan
Suhdelaskenta ei kuitenkaan perustu käänteistietoon ja siitä johdettuun tietoon. Laskenta perustuu vertaistiedosta määritettävään arvoon. Matematiikkaa ei joissakin tapauksissa lasketa luonnontieteisiin, joskus sen edes yrittämättä soveltaa sitä maailmankuvaan. Tämän kuvauksen antoi Nobel-palkittu fyysikko ja matemaatikko, Richard Feynman. Tämän hän on todennut tehtyään ihmisen määrittämän tarkimman luonnonkuvauksen. Richard Feynmannista on silti muistettava, hänen ilkikurinen pilke silmäkulmassa.
Varmuudella voi sanoa olevan menettelyn tiedon hakemiseksi käänteistietoon perustuvana, jolla tarkoitetaan joukko-oppia. Vastaava menettely käsitteellisten ja käsin kosketeltaviin asioiden määrittämiseksi, on suhdelaskentamenettely. Joukko-oppi antaa kuvan ongelmasta tai etsittävästä tiedosta, suhdelaskennan antaessa usein tarkan laskennan tuloksen. Tuotteet sivuillani, ovat todiste laskennasta ja laskennan syntymisestä. On helpompi uskoa laskentaan, josta löytyy taulukoitua tietoa, malleja maailmassa ja yhtenäinen kuvaus asioiden välille. Suhdelaskenta on tarinaa, historiaa ja luovuutta. Laskennan erilaisen käsittelytavan seurauksena syntyy jotain, jota muuten ei saa. Laskennassa ei edetä johdonmukaisesti tunnettua kohti, kuten tunnetun opettajat koulussa tekevät. Suhdelaskennassa edetään tunnetun kautta tuntemattomaan. (7)
4. Suhteellisuus yleisesti

Suhteellisuudessa kappaleet näyttävät samalta, mikäli suhteesta ei ole tietoa. Kuvassa olevat nostokorvakkeet ovat esimerkki suhteellisuudesta.
Nostokorvakkeiden koko on riippuvainen siitä, kuinka kaukaa niitä tarkastellaan ja tiedetäänkö tarkastelun etäisyys. Nostokorvakkeet ovat tietyllä etäisyydellä tarkastelijaan nähden, mutta myös toisiinsa nähden kokona ja arvoina tuotteen sisällä.
Pienin ja suurin korvake kauempaa katsottuna ovat saman näköisiä ja vertaamattomia korvakkeiden kesken. Tämän voi havaita kuvasta oikealla, jolloin korvakkeista ei voi arvioida niiden kokoa tai nostokapasiteettia.
Nämä nostokorvakkeet ovat nostokyvyltään 500 - 40 000 kg ja niiden lujuus on mitoitettu samaan jännitystasoon. (1092)
5. Suhdelaskennan etuja
Suhdelaskennalla laskentamenettelynä on paljon annettavaa tehtävissä, joita ei muulla tavalla saa selville. Luonnollisesti laskentatulos ei saa poiketa muulla tavalla määritetystä. Arvoja lähestytään ainoastaan poikkeavasti toisesta suunnasta, kuin totutusti. Laskenta antaa näkemystä fysiikkaan, fysiologiaan ja materiaan, sekä luo ymmärrettävän samaa tarkoittavuuden asioihin ja arvoihin.
- laskennan tuloksen suhteellinen siirtämismahdollisuus
- teknisen suunnitelman painotehokkuusvertailut
- tuotteiden vertaamismahdollisuus
- materiaalien ja tuotteiden vakioituminen
 jatkuvuus tuotteisiin ja niiden ideointiin jatkuvuus tuotteisiin ja niiden ideointiin- tuntemattoman arvon määrittäminen
- laskimella todennettava laskenta
- jatkuva luonnonmukainen prosessi
- tunnetut tieteen mukaiset arvot
- käsitteet lujuudelle ja käyttöiälle
- johdonmukainen laskentatapa
- tieteitä yhdistävä menettely
- yhtenäinen maailmankuva
- yhtenäinen mitoitustapa
- yksinkertainen laskenta
- nopeuttaa laskentaa
- ymmärrettävyys
Suhdelaskenta on rinnakkainen tapa tarkastella asioita ja ilmiöitä, kattaen kaiken. Ilman suhdelaskentaa, jää havaitsematta suhteellisuus ilmiöissä. Tämä on hyväksyttävää, sillä kaikkien ei tarvitse ymmärtää tapahtumien muodostumista. Suhdelaskenta ei ole edes vaikeaa, joskin syvällistä ajattelua vaativa. Lopulta laskentatulokset ovat tarkistettava ympäröivä todellisuus. (266)
6. Suhdelaskennan suureet
 Fysiikassa, lujuuslaskennassa ja eri asioiden yhteydessä yksiköiden tulee olla yhteismitallisia. Tämä tarkoittaa SI-järjestelmää tehtäviä ratkaistaessa, joka koostuu seitsemästä perusyksiköstä suureille. Pituus, massa, sähkövirta, aika, lämpötila, ainemäärä ja valovoima. Fysiikassa, lujuuslaskennassa ja eri asioiden yhteydessä yksiköiden tulee olla yhteismitallisia. Tämä tarkoittaa SI-järjestelmää tehtäviä ratkaistaessa, joka koostuu seitsemästä perusyksiköstä suureille. Pituus, massa, sähkövirta, aika, lämpötila, ainemäärä ja valovoima.
Laskentaa ei voi tehdä, mikäli laskeminen ei toteudu yksiköiden muodossa. Tämän vuoksi on mietittävä mitä yksiköitä laskennassa käytetään. Tämän jälkeen laskennassa havaitaan matemaattinen harmonia, sillä tapahtumat ovat alkuräjähdyksestä ja käsiteltäviä energialausekkeiden kautta.
Taulukoiduista suureista monet liittyvät energiaan.
Massa m kg kilogramma
Aika t s sekunti
Sähkövirta I A ampeeri
Termodynaaminen lämpötila T K Kelvin
Ainemäärä n mol mooli
Valovoima l cd kandela
CGPM yleinen paino- ja mittakonferenssi
Muut paitsi kilogramma ovat määritetty perustuen luonnonilmiöihin. Kilogramma (kg) perustuu Ranskassa 1700-luvun lopussa määritettyyn prototyyppikappaleeseen. Suhdelaskenta laajentaa laskennan käsitettä yllä olevissa suureissa. Laskennassa kg arvo muutetaan kertoimen 9,82 avulla arvoksi N (Newton = 0,102 kg). Arvo 1 kN tarkoittaa käytännössä 100 kg massaa.
Tarvittaessa, yksiköt suhteutetaan laskentaan sopivaan muotoon, fysiikan antaman mallin mukaisesti. Taulukoiden avulla on mahdollista laskea suhdelaskennan tehtäviä muuntamatta yksiköitä. Esimerkiksi 1 maili 1,609 km on kultaisen leikkauksen mittasuhteessa (1,618) kilometriin nähden (virhe 0,0055 %).
Tuuma 2,54 cm on 1,6182 = 2,618 (virhe 0,03 %).
2,618 / 1,03 = 2,54
Joissakin tapauksissa virhe määrittyy 0,03 prosentiksi eli staattisen väsymisen kertoimeksi 1,03. Tämä on aikadilaation arvo nopeudella 0,25 x c, joka liittyy lähes kaikkeen laskemiseen ilmiöissä. Hallitsemalla suhdelaskennan, mittamuunnoksia ei aina tarvita eri yksiköillä laskettaessa. Tämä edellyttää kylläkin tietoisuutta arvojen muodostumisesta. (315)
7. Newtonin kokeellinen filosofia

Vain sellaiset syyt ovat hyväksyttäviä, jotka ovat tarpeellisia ilmiöiden selittämiseksi.
Samankaltaiset ilmiöt pitää aina selittää, siinä määrin kuin mahdollista, samalla syyllä.
Sellaisia kappaleiden ominaisuuksia, jotka eivät voi lisääntyä eivätkä vähetä ja jotka kuuluvat kaikille kappaleille, joilla voidaan tehdä kokeita, on pidettävä kuuluvina kaikille kappaleille yleisesti.
Kokeellisessa filosofiassa ilmiöistä pääteltyjä lainlaisuuksia on pidettävä vastakkaisista hypoteeseseista huolimatta täsmälleen tai suurin piirtein oikeina, kunnes toiset ilmiöt vahvistavat ne kokonaan tai näyttävät, että ne ovat taipuvaisia poikkeuksiin. Sillä hypoteesi ei voi heikentää kokemuksen perusteella tehtyä päätelmää.
Nämä pätevät tänään ja tulevaisuudessa. (790)
8. Diofantoksen muistokirjoitus
Muistokirjoitus on lyhyt teksti vainajan kunniaksi. Kreikkalaisen algebran isä, Diafantos Aleksandrialainen syntyi vuosien 200 - 214 Ekr. välillä ja kuoli vuosien 285 - 299 Ekr. välillä, eläen 84-vuotiaaksi. Esimerkki osoittaa tavan määrittää elämän pituus suhteellisina pituuksina ja kuinka arvoituksen kaltaisen tehtävän voi ratkaista. Hänestä ei tiedetä paljoa, mutta ikä tiedetään hautakiveen kaiverretun ongelman ansiosta.
Jumala salli hänen elää kuudesosan poikana ja seuraavan kahdestoistaosan aikana Hän kasvatti hänelle parran. Hän sytytti hänelle avioliiton valon seitsemäsosan jälkeen. Viisi vuotta hänen naimisiinmenonsa jälkeen Jumala soi hänelle pojan. Mutta voi, säälimätön Kohtalo otti pojan, kun tämä oli iältään puolet siitä, jonka hänen isänsä saavutti. Lohdutettuaan itseään lukujen tieteellä neljä vuotta hän siirtyi pois tästä elämästä.
Samalla tavalla, kuin hautakivi kertoo Diafantoksen iän, kertoo luonto asioiden kautta tiedon. Määritämme ensin Diafantoksen iän.
L/6 ajan elämästään hän vietti poikana
L/12 hän eli nuoruuttaan
L/7 hän eli tämän jälkeen ennen avioitumistaan
5 vuotta myöhemmin syntyi hänen poikansa
L/2 oli pojan ikä
4 vuotta kului ennen kuin hän itse kuoli
L = L/6 + L/12 + L/7 + 5 + L/2 + 4
L = 14L/ 84 + 7L/84 + 12L/84 + 5 + 42L/84 + 4
Diofantoksen eliniäksi tulee 84 vuotta ja poika kuoli 42 vuoden ikäisenä.
L = 75L/84 + 9
3/28 L = 9 => L = 28/3 x 9 = 84 vuotta
(Tammi: Fermat'n viimeinen teoreema, Simon Singh) (309)
9. Arvojen muodostuminen
9.1 Konkreettiset arvot
Arvot syntyivät alkuräjähdyksen yhteydessä. Mitattavia, käsin kosketeltavia arvoja ovat kappaleen pituus, leveys ja korkeus. Nämä ymmärretään parhaiten kappaleeseen liittyvinä mittoina.
Ominaisuuden käsin kosketeltavalle antaa siihen sisältyvä arvo. Arvoa voi kutsua varjoksi, sillä sekin muodostuu konkreettisesti olevasta. Kivellä ja kävyllä voi heittää kohdetta. Kävyn keveys ja pehmeys tekevät siitä todennäköisemmän valinnan, halutessa olla satuttamatta tai rikkomatta. Suhdelaskenta mahdollistaa käsitteellisen, käsin koskemattoman arvon tarkastelun. Tietokoneella luodaan kolmeulotteisia näköismalleja, jotka ovat katsottavia, mutta ei kosketeltavia. Mallista ei tästä johtuen tiedä, miltä ne tuntuvat. Arvot ovat yksiulotteisia, tarkoittaen arvolla saatavaa tietoa kohteesta, kuten pituus, paino, kovuus, lämpö, taipuma jne. Alla olevaan viisikulmioon, käsin kosketeltavat arvot muodostavat alaosan kolme särmää.
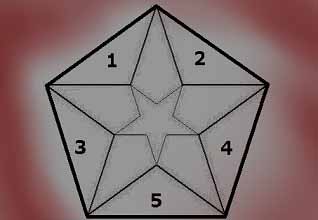
1. Suhteellisuus
2. Aika
3. Pituus
4. Korkeus
5. Leveys
9.2 Abstraktiset arvot
Alkuräjähdyksen yhteydessä syntyi arvoja, joita ei näe, kuten aika. Ajan käsite on suhteellista, kuten se yleisesti mielletään. Toisissa asioissa tietty ajanjakso on pitkä, toisissa lyhyt. Näin myös eri henkilöiden tarkastellessa asioita, ne nähdään eri mittakaavassa ajan suhteen. Suhteellisuus on toisinaan suoraan verrattavaa, toisissa tapauksissa käsitteellisesti ymmärrettävää.
Esimerkkinä voimme valita halutut mittasuhteet. Valittuamme muodon, voi todeta vaikkapa tangon painavan 1 kg/m. Sahattaessa 2 m pitkä kappale tangosta, on valittu pituus, mutta ei siihen sisältyvää painoa. Painoksi tangolle tulee aina 2 kg saman mittaisessa kappaleessa. Saman kaltainen tilanne syntyy lukemattomissa asioissa, sillä tiedostamatta arvon määrittämällä, muutkin arvot määrittyvät.
Katkaise 0,1 m pituinen tanko ja aseta se tukien väliin, todeten tanko jäykäksi. Sahaa toinen tanko kaksi kertaa pitempänä, jolloin se vastaavasti tukien päällä taipuu noin kaksi kertaa enemmän. Voitteko sanoa, paljonko tanko taipuu 42 m pitkänä? Toteatte, ettei sellaista tangon pituutta ole. Sanotte tangon taipuvan kahdeksankertaisesti, kun jänneväli kasvaa kaksinkertaiseksi. Jännevälin vaikutus taipumaan, on kaavassa kolmanteen potenssiin. Tässä olette väärässä, sillä tarvitsee vain muuttaa ajatusten kulkua. 100 m pikajuoksija on jäykkä kuten esimerkin tanko, väsymättä eli taipumatta sadan metrin matkalla. Juoksija ei väsy myöskään 200 m matkalla, jolloin suoritukseen kuluva aika on kaksi kertaa sadan metrin juoksuun käytetty aika. Juoksija kykenee myös maratonin matkaan, taipuen ajan lisääntymisenä. Molemmat juoksut ovat laskettavaa arvoina.
Viisikulmio kuvaa suhteellisuutta. Esitetyssä viisikulmiossa on kolme määritettävää ulotteisuutta eli pituus, leveys ja korkeus. Muuttuva aika (dilaatio) liikkuvaan ja paikalla pysyvään, sekä kiinteä suhteellisuus. Näiden kautta menettely on laskettava todellisuus. Jotkut asiat ovat etenemää, toiset pinta-alaa ja eräät tilavuuteen perustuvaa laskentaa. Tehtävän voi usein laskea ristiin monessa merkityksessä.
Entä aika? Kaikella on vastapari kuten kylmä - kuuma, valkoinen - musta jne. Aika liitetään ilmiön kuvaamiseen ja mielletään liikkeeseen. Samaa tarkoittavassa suhdelaskennassa ei niinkään sekunteina, vaan aikadilaationa. Näin aikaa tarkastellen, se liittyy aika-avaruuteen, yhtä hyvin kuin arvoavaruuteen tuotteissa ja ilmiöissä. (258)
10. Kultainen leikkaus 1,618 laskenta
Φ + 1 = Φ x Φ Φ (fii) = 1,618
Φ2 - Φ - 1 = 0 Φ2 = 2,618
Suhdeluku 2,618 muodostuu, kun ympyrän sisään piirretään ellipsi ja näiden suhde toisiinsa on kultaisen leikkauksen suhdeluku 1,618. Pythagoras tarkasteli pyöreätä muotoa, mutta luopui muodon tarkastelemisesta hankalien lukujen vuoksi? Suhdeluvulla on yhteys lujuuden muodostumiseen kuormitustapauksissa.
ax2 + bx + c = 0
NJR = neliöjuuri
x = -b ± NJR (b2 - 4ac )
2a
a = 1
b = -1
c = -1
Φ = 1 ± NJR ( 5)
2
Φ = 1,6180339887498948482045868343656
NJR (5) = 2,2360679774997
1 + 2,2360679774997 = 1,61803398874989
2
1 - 2,2360679774997 = 0,61803398874989
2
Φ = 2 cos (Pii /5) (radiaaneissa)
Φ = 0,5 sec (2 pii / 5)
Φ = 0,5 csc (pii / 10)
Samaa tarkoittava suhdelaskenta
1,032 = 1,06 => 1,062 = 1,12 => 1,122 = 1,25 => 1,252 = 1,56 => 1,56 x 1,03 = 1,618 => 1,6182 = 2,618 => 2,618 -1 = 1,618 => 1,618 -1 = 0,618 => 0,618 x 1,618 = 1 => 0,618 / 1,618 = 0,382 => 0,382 + 0,618 = 1 => 4 x 1,618 /1,03 = 6,28 => 1,618 x 2 /1,03 = 3,14
Suhde 1,618 on mielenkiintoinen, kuten esimerkit osoittavat. Näitä ei tarvitse opetella. Riittää, että tutustuu niihin. Fibonaccin lukujono liitetään myöhemmin kultaiseen leikkaukseen. Kultainen leikkaus on kiinnostanut vuosituhansia matemaatikkoja, lukujen avautumatta niitä tutkimalla. Tuotteita tarkastellen lukusuhteet avautuvat kuitenkin uudella tavalla. Tämä edellyttää ainoastaan tuotteiden tuntemisen. (222)
11. Numerot vastaan suhdelaskenta
Roomalaiset Arabilaiset Laskennan kertoimet
I 1 1,00 (1,03 - 1,06 - 1,12 )
II 2 1,25
III 3 1,60
IIII 4 2,50
IV 5 3,15
VI 6 4,00
VII 7 5,00
VIII 8 6,30
IX 9 8,00
X 10 10,00
1 x 10 = 10 1,0 x 10,00 = 10
2 x 5 = 10 1,25 x 8,00 = 10
1,60 x 6,30 = 10
2,00 x 5,00 = 10
2,50 x 4,00 = 10
3,15 x 3,15 = 10
Laskee:
+ numerot + numerot - numerot
- suhteellisuus - suhteellisuus + suhteellisuus
- käsitteellinen + käsitteellinen + käsitteellinen
- (konkreettinen) + kokreettinen + konkreettinen
- ei kaavoihin + kaavoihin - ei kaavoihin
- ei hahmota arvoa - ei hahmota arvoa + hahmottaa arvon
Lähdemme liikkeelle samasta ja lopetamme samaan, sillä vain tapa tarkastella asioita poikkeaa. Emme laske aritmetiikkaa, laskemme ilmiöitä. Voimme laskea asioita, joita aritmeettiset numerot eivät kykene esittämään, kuten viitteellisesti näkee yllä olevista laskelmista. Kultaisen leikkauksen arvoa (1,618), matematiikka ei edes tunne käytännössä. Roomalaisilla ja arabialaisilla numeroilla voi vaikkapa kerätä veroja, mutta suhdelaskentana se ei onnistu. Suhdelaskenta puolestaan voi määrittää vaikkapa käyrän tunnetun tietojoukon perusteella. Käyrän, jota kenties ei ole kokeilla määritetty. (759)
21. Viisi ensimmäistä suhdelaskennan kerrointa
1 - 1,03 - 1,06 - 1,12 - 1,25 - (1,618)
1,00 x 1,00 = 1,00 => 1,00 + 1,00 = 1,00 => 1,00 / 1,00 = 1,00
1,03 x 1,03 = 1,06 => 1,03 + 1,03 = 1,06 => 1,06 /1,03 = 1,03
1,06 x 1,06 = 1,12 => 1,06 + 1,06 = 1,12 => 1,12 /1,06 = 1,06
1,12 x 1,12 = 1,25 => 1,12 + 1,12 = 1,25 => 1,25 /1,12 = 1,12
käyttäkää laskukonetta
Unohtakaa desimaalit
1 on jotakin, joka tunnetaan
Kaksi samaa tunnettua yhdessä on 1
(1 x 1 =1)
Onko laskelmissa jotakin väärin? Kertomalla ja yhteen laskemalla ei saa samaa? Suhdelaskennan suhdeluvut ovat siksi poikkeukselliset. Ominaisuus, jossa laskennan tulos on seuraava kerroin, tekee laskentamenettelystä ainutlaatuisen. Luku 1 on jotakin, joka tunnetaan. Pilkun takana on kerroin. Laskelmana 1,03 + 1,03 = 1,06 ja 1,03 x 1,03 = 1,06.
 Viisi ensimmäistä kerrointa ovat laskettavaa. Kuudes on kultaisen leikkauksen suhdeluku 1,618, jonka saa maailmankaikkeuden kitkan (1,03) avulla. Kultainen leikkaus 1,618 ei ole suoraan laskettavissa. Siinä menettämättä mitään, sillä laskenta hahmotetaan kertoimeen 1,03(4) suhteellisuusteorian energiakaavan aikadilaatioon. Kertoimen 1,03 löytää pyramideista tuhansia vuosia sitten, päätyen näkemisen geometrian muotoihin. Viisi ensimmäistä kerrointa ovat laskettavaa. Kuudes on kultaisen leikkauksen suhdeluku 1,618, jonka saa maailmankaikkeuden kitkan (1,03) avulla. Kultainen leikkaus 1,618 ei ole suoraan laskettavissa. Siinä menettämättä mitään, sillä laskenta hahmotetaan kertoimeen 1,03(4) suhteellisuusteorian energiakaavan aikadilaatioon. Kertoimen 1,03 löytää pyramideista tuhansia vuosia sitten, päätyen näkemisen geometrian muotoihin.
(0,25 = 1,25)
1,25 x 1,25 x 1,034 = 1,618 => 1,618 /(1,25 x 1,25 x 1,034) = 1,25
Kitka 1,034 liittyy kertoimeen 1,25, joka esitetään esimerkeissä. Kerroin 1,1(2) on materiaan ja energiaan liittyvää, kaiken liittyessä saumattomalla tavalla toisiinsa. Taiteilijat ja arkkitehdit tuntevat suhdeluvun 1,618. Sen merkitys avautuu laskennan myötä kaikkia koskevaksi. (445)
22. Fibonaccin lukujono
0
1 1
1 2 1 Pascalin kolmio
1 3 3 1
Viides rivi 1 4 6 4 1 16 = 1,618
0 - 1 - 1 - 2 - 3 - 5 - 8 - 13 - 21 - 34 - 55 (Tuplavitonen- Double five)
Fibonaccin lukujonon ensimmäiset yksitoista lukua järjestyksessä
Joskus Fibonaccin lukujono määritetään alkavan ykkösestä, ei nollasta. Kaksi ensimmäistä numeroa Fibonaccin lukujonossa ovat 0 ja 1 ja seuraavat numerot ovat kahden edellisen numeron summa. Havaitaan Fibonaccin lukujonon alkavan, kuten Pascalin kolmio.
Suhde kultaiseen leikkaukseen
1/1 = 1,000 Tämä on enemmän näkemisen geometriaa kuin matematiikkaa
3/2 = 1,5000
5/3 = 1,666...
8/5 = 1,600
13/8 = 1,625
21/13 = 1,615 Arvo lähenee lopulta tarkaksi arvoksi
34/21 = 1,619
55/34 = 1,617647
89/55 = 1,6181818
...... = ...............
Kultainen leikkaus 1.61803398874989
Paskalin kolmio 1 Pascal's Triangle
Yhdestoista rivi on 1,618 1 1 The Eleventh row is 1,618
Lopulta ilmiöt noudattavat kuvatun kaltaista lukujen muodostumista, kukin omalla tavallaan. Pascalin kolmio on kuvio, joka sisältää olevaisen muodostumisen kuvauksen. (397)
23. Pascalin kolmio
Blaise Pascal ei keksinyt kuviota, koska jo muinaiset kiinalaiset tunsivat sen. Pascal havaitsi kuitenkin kolmion käyttökelpoisuuden matemaattisissa ongelmissa. Suhdelaskennan kannalta on tärkeää, että rivit ovat laskettavaa kuudenteen riviin saakka. Kuudennen rivin jälkeen, luvut karkaavat käsityksestä. Kuudennen rivin puolikkaan summa, on suurella tarkkuudella kultaisen leikkauksen suhdeluku 1,618. Yhteenlaskemalla viidennen rivin summa on luku 16. Tämä on kreikkalaisten aakkosten 16. kirjain fii, luvun 1,618 tunnus.
 Tutkimusten mukaan ihmiset pystyvät hallitsemaan korkeintaan viisi saman aikaista tapahtumaa ja eräissä tapauksissa lahjakkaimmat kymmenen tapahtumaa. Samaa ajatusta voi käyttää suhdelaskentaan. Luku viisi suhdeportaina, on suhteellisuusraja. Tutkimusten mukaan ihmiset pystyvät hallitsemaan korkeintaan viisi saman aikaista tapahtumaa ja eräissä tapauksissa lahjakkaimmat kymmenen tapahtumaa. Samaa ajatusta voi käyttää suhdelaskentaan. Luku viisi suhdeportaina, on suhteellisuusraja.
Pascalin kolmiosta sanotaan jokaisen rivin summan kasvavan kertoimella 11=> 1 x 11 = 11 => 11 x 11 = 121, joka voi havaita taulukosta. Luonnossa ole kertoimella 11 esiintyvää. Kertoimella 1,1 sen sijaan on yhteys luonnossa tapahtuviin ilmiöihin ja suhdelaskenta perustuu osittain tähän kertoimeen, varsinkin taipuman yhteydessä. (325)
1,1
1,1 x 1,1 = 1,21
1,1 x 1,1 x 1,1 = 1,331
1,1 x 1,1 x 1,1 x 1,1 = 1,4641
1,1 x 1,1 x 1,1 x 1,1 x 1,1 = 1,61051
23.1 Pascalin kolmion alin rivi
Pascalin kolmion alin rivi vastaa kultaisen leikkauksen suhdelukua 1.618, jolloin havaitsee sen poikkeavan arvosta. Osoitan arvolla 1,611 olevan sama merkitys arvon 1,618 kanssa.
1 1,000
1 1 1,1 x 1,0 = 1,100
1 2 1 1,1 x 1,1 = 1,210
1 3 3 1 1,1 x 1,21 = 1,331
1 4 6 4 1 1,1 x 1,331 = 1,464
1 6 1 1 6 1 1,1 x 1,4641 = 1,611
Pascalin kolmio liittyy maan painovoiman aiheuttamaan kiihtyvyyteen 9,82 m/s2.
9,82 / 6,28 = 1,56
Painovoiman kiihtyvyys maapallon pinnalla jaettuna täysympyrän kulmalla kaksi kertaa pii radiaania (6,28 radiaania) ==> kiihtyvyyden aiheuttama väsymisen pinta-ala arvoltaan 1,56. Lähtökohta 9,82 m/s2 on epätarkka, sillä tiede tuntee gravitaation huonosti.
1,56 x 1,03(3) = 1,611
 Juoksemisessa ja minkä tahansa ilmiön yhteydessä tapahtuu väsymistä, joka aiheuttaa suhteellista ajan tai vaihtoehtoisesti taipuman lisääntymisen etäisyyden kasvaessa. Tässä vaikuttaa staattisen väsymisen kerroin 1,03(3). Kiihtyvyyden aiheuttaman väsymisen pinta-ala 1,56 kertaa staattinen väsymisen kerroin 1,03(3) on Pascalin kolmion alin rivi arvoltaan 1,611. Juoksemisessa ja minkä tahansa ilmiön yhteydessä tapahtuu väsymistä, joka aiheuttaa suhteellista ajan tai vaihtoehtoisesti taipuman lisääntymisen etäisyyden kasvaessa. Tässä vaikuttaa staattisen väsymisen kerroin 1,03(3). Kiihtyvyyden aiheuttaman väsymisen pinta-ala 1,56 kertaa staattinen väsymisen kerroin 1,03(3) on Pascalin kolmion alin rivi arvoltaan 1,611.
1,252 x 1,03 = 1,611
Väsymisen ja vahvistumisen kaksinkertaistu-misen kerroin on 1,25, jota käytetään laakereiden kestoiän, sekä fysiologisen vanhenemisen laskemiseen. Kerroin littyy myös koneenrakennuksen lujuuteen. Suhdelaskenta ei ole desimaaleja, vaan kokonaisuuden hahmottamista.
24. Nollan historia
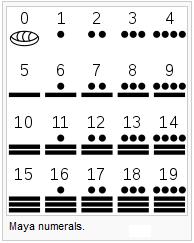 Maya-intiaaneilla egyptiläisten tapaan oli taitavasti suunniteltu aurinkokalenteri. Tämä poikkesi edistyksellisyydessä siitä kalenterista, minkä maan valloittaneet eurooppalaiset toivat tullessaan. Mayoilla oli numero nolla, jota ei ollut eurooppalaisen kalenterin tekemisessä. Maya kalenteri alkoi elokuun 11 tai 13 päivä 3114 vuotta ennen ajanlaskua. Maya-intiaaneilla egyptiläisten tapaan oli taitavasti suunniteltu aurinkokalenteri. Tämä poikkesi edistyksellisyydessä siitä kalenterista, minkä maan valloittaneet eurooppalaiset toivat tullessaan. Mayoilla oli numero nolla, jota ei ollut eurooppalaisen kalenterin tekemisessä. Maya kalenteri alkoi elokuun 11 tai 13 päivä 3114 vuotta ennen ajanlaskua.

Maya numerals
Nollan puuttumisen seurauksena länsimaissa ei aina tiedetty, minä vuonna vuosituhat vaihtui. Siitä sai esimakua muutama vuosi sitten esiintyneistä keskusteluista. Unohdimme sen jo vai? Länsimainen Gregoriaaninen kalenteri on esitelty vuonna 1582.
Gregorian calendar
Alla mayojen toinen tapa merkitä numeroita. Kuva on kirjasta, mutta numerot ovat tunnettua tietoa. Maya numero nolla ylemmässä kuvassa muistuttaa tämän päivän amerikkalaisen jalkapallon pelivälinettä palloa. Nolla on jotakin todellista, kuten syntymäpäivä mille tahansa. On olemassa jotakin, mutta sillä ei ole vielä ikää eikä arvoa. Emme tarvitse ilmausta olemassa olemattoman olevaisuudesta. Pallo peliin ja tilanne on aluksi 0 - 0.

Charles Seife
nollan elämäkerta
Suomentanut Risto Varteva
Werner Söderström Osakeyhtiö vuonna 2000
The Biography of a Dangerous Idea
 Charles Seife Charles Seife
Ajatus kuvallisessa muodossa olevasta laskennasta on ihailtava. Länsimaissa vastaava liittyy pelikortteihin, joissa kortin arvoa kuvataan Jokerina, kuninkaana, kuningattarena jne. Suhdelaskenta ei laske numeroita, vaan ilmiöitä kertoimilla. Ensimmäinen kerroin, toinen kerroin .... kokonaisuus 1. Kokonaisuus ei ole kerroin, sillä 1 x 1 on edelleen 1. Toisaalta 0 x 0 on vastaavasti 0. Asioilla on vastakkainen puolensa, kuten virralla laitteessa pois - päällä, sillä sitä nollalla ja ykkösellä toisinaan kuvataan. Nollaan perustuva laskeminen liittyy mielikuvituksellisiin imaginaarilukuihin, johon harva kykenee. Aikaa varmasti vierähtää miettiessä vaikkapa nollan neliöjuuren olemusta. Ykkönen on esitettävässä laskennassa rautakanki, jolla arvo kammetaan arvoavaruudesta. Arkimedes teki vipuamisen käsin kosketeltavalle, nyt se mahdollista käsin koskettamattomalle arvolle. Rautakanki käsin kosketeltaville asioille, mielikuvitustanko käsin koskettamattomille asioille. Laskennan perustuessa energiakaavaan E = m c2, on valon nopeus suurin saavutettava nopeus c= 1 = 300 000 km/s mutta ei yli tämän nopeuden.
1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 0
0,125 - 0,16 - 0,2 - 0,25 - 0,315 - 0,4 - 0,5 - 0,63 - 0,8 - 1 ( , = . )
 
Fibonacci numero nolla
 Leonardo Fibonaccin (1189 - 1250) ollessa nuori, hän matkusti isän kanssa, joka oli italialainen liikemies. Matkoilla he ylittivät Välimeren ja tapasivat arabialaisia myyjiä. Leonardo oppi kielen ja tutustui arabialaiseen tapaan laskea. Leonardo Fibonaccin (1189 - 1250) ollessa nuori, hän matkusti isän kanssa, joka oli italialainen liikemies. Matkoilla he ylittivät Välimeren ja tapasivat arabialaisia myyjiä. Leonardo oppi kielen ja tutustui arabialaiseen tapaan laskea.
Roomalaiset "tikkunumerot" olivat hankalia laskettaessa, eikä numeroihin kuulu nollaa tarkoittavaa, ei mitään merkintää. Mitä roomalaiset tekivät, oli jättää tyhjä paikka nollaa merkitsevään kohtaan. Näin laskeminen roomalaisilla numeroilla oli mahdollista. Ymmärrämme arabialaisen tavan laskea olleen paremman. Aikuisena hän opetti Bolognan yliopistossa, Italiassa.
 Fibonacci Fibonacci
Jotta asia ei ole liian helppo, numero 0 ei tullut Arabiasta. Intialaiset kehittivät numero nollan käytön laskennan yhteydessä. Fibonacci opetti yhdeksän intialaisen numeron olevan 9 8 7 6 5 4 3 2 1. Yhdeksällä numerolla ja merkinnällä 0, mikä tahansa numero voidaan merkitä. Näin kirjoittaen, kuulostaa kuin Fibonacci ei olisi ymmärtänyt nollaa numeroksi.
Ymmärrämme numero nollan. Kuinka käy laskettaessa vuosia, jos ei ole vuotta 0 ennen ja jälkeen ajanlaskun kalenterissa. Yksi vuosi ennen ajanlaskua, muuttuu vuodeksi 1 jälkeen ajanlaskun. Aikalaskelman yhteydessä -30 vuonna syntynyt poistuu keskuudestamme +25 vuonna. Kuinka vanha hän oli kuollessa? (+25) - (-30) = 55 vuotta. Menikö oikein? Mihin sijoittui vuosi nolla?
Fibonaccin lukujono alkaa nollasta 0 - 1 - 2 - 3 - 5 - 8 ... Voimme lukea näiltä sivuilta lukujonon liittyvän kultaisen leikkauksen suhdelukuun. Entä luonnollisen logartimin irrationaalisen e arvon muodostuminen?
e = 2.71828 18284 59045 23536 (lyhennettynä 20 desimaaliin)
arvon e muodostuminen
e = 1/0! + 1/1! + 1/2! + 1/3! + 1/4! + 1/5! + 1/6! + ....
Symboli ! merkitsee kertomaa, 5! tarkoittaen 1x2x3x4x5. 1! on arvoltaan 1. 0! voidaan määrittää arvoksi 1 yhtä hyvin.
Mayat kehittivät paikkasidonnaisen numerointijärjestelmän, käyttäen numero nollaa. Tätä ei liittynyt eurooppalaiseen numerointijärjestelmään. Ilman numero nollaa, nykyaikainen matematiikka olisi mahdotonta. Voi sanoa numero nollan olevan paikanpitäjän.
Suhdelaskenta on mayojen paikkasidonnaisen numerointijärjestelmän kaltainen, mutta tarkastelee lukujen sijaan arvoja ja ilmiöitä. Nyt emme tiedä, mikä numero 1 on. Kun meillä on omena, sanomme meillä olevan omenan. Antaessamme sen pois, meillä ei ole yhtään omenaa. Huomioimme nollan olevan ei mitään, mutta numeron. Samoin kuin Englannin kielessä, sanomme yhtään sanaa jälkeen omenan monikossa, omenaa = kolme omenaa. Vrt. pala omenaa, jolloin pala ei liity tarkasteltavaan joukkoon.
Palaamme historiassa taaksepäin. Intialainen matemaatikko Brahmagupta ymmärsi nollan olevan todellisen luvun ja antoi laskentaohjeen käytöstä vuonna 628 jälkeen ajanlaskun. Jokin joka ei ole mitään, kuuluu johonkin joka meillä on. Ajatus liittyy suhdelaskentaan, sanoessa jonkin jota emme voi koskea, liittyvän johonkin, johon voimme koskea. Numero nolla on jotakin, jota emme voi koskea. Numero yksi on jotakin, jota voimme koskea tai voimme näin ymmärtää. Numero nolla on kuten piste kirjoituksessa. On mahdollista kirjoittaa teksti pisteitä käyttämättä, mutta mitä tapahtuu lukiessa?  (536) (536)
Zero
25. Numero viisi suhdelaskennassa
 Laskenta tutustuttaa viisikulmioon ja kirjoituksiin Pythagoraasta? Useassa kirjassa varoitetaan tämän kaltaisesta ajattelusta, ikään kuin numeroihin tai kuvioihin sisältyisi matemaattisen olion käsite. Silti muutama nimi Leonardo da Vincistä eteen- ja taaksepäin ovat huomioitava numero viisi ja suhdeluvun 1,618 yhteydessä. Näkemisen geometria on laskennallinen todellisuus, josta on kirjoitettu. Laskenta tutustuttaa viisikulmioon ja kirjoituksiin Pythagoraasta? Useassa kirjassa varoitetaan tämän kaltaisesta ajattelusta, ikään kuin numeroihin tai kuvioihin sisältyisi matemaattisen olion käsite. Silti muutama nimi Leonardo da Vincistä eteen- ja taaksepäin ovat huomioitava numero viisi ja suhdeluvun 1,618 yhteydessä. Näkemisen geometria on laskennallinen todellisuus, josta on kirjoitettu.
Seuraavan kirjoittamani liittymättä mitenkään aiheeseen, liitän sen tästä huolimatta tähän. Minusta on vain hauska tehdä se tässä yhteydessä. Tiedätte Leonardo da Vincin tunnettuna taiteilijana ja pystytte luettemaan hänen teoksiaan. Tehkää se nyt, jolloin toteatte sen saman tien mahdottomaksi. Muutama säilynyt maalaus (n. 15 kpl) hänen muistiinpanojensa ohessa, joihin kuuluu piirustuksia, tieteellisiä kaavioita ja ajatuksia maalaustaiteen luonteesta, muodostavat merkittävän panostuksen myöhemmille taiteilijoille, jolloin sen kanssa kilpailee vain hänen aikalaisensa Michelangelo. Leonardo da Vinci oli siten eräs maalaustaiteen merkittävimmistä taiteilijoista, olematta varsinaisesti taidemaalari. Onko kenties käsityksenne ilmiöistä samaa tasoa tietämyksenne kanssa Leonardo da Vincistä? Tiedätte paljon, mutta ette tiedä kaikkea. Kenties tahdotte lukea lisää kirjoittamaani. Mikäli laskukone kädessänne ei esitä samaa kuin kirjoitan, poistukaa sivuiltani. Suon sen teille mielihyvin, siirtyäksenne takaisin fantasian maailmaan. Edellinen lause, sillä uskon laskimen kertovan enemmän todellisesta maailmasta, kuin aatemaailmat yhteensä todistamattomina.
Ympyrän pinta-ala
a) Säde - r = 1
A = π x r2 = 3,14
b) Säde - r = 2
A = π x r2 = 12,566
Täysympyrä 360o
2 x π rad =6,28 rad.
1 - 1,03 - 1,06 - 1,12 - 1,25 - 1,6 - 2 - 2,5 - 3,15 - 4 - 5 - 6,3 - 8 - 10
6,283 rad / 2 = 3,14 rad
1 - 1,03 - 1,06 - 1,12 - 1,25 - 1,6 - 2 - 2,5 - 3,15 - 4 - 5 - 6,3 - 8 - 10
3,14 rad / 2 = 15707
1,5707 rad => 1,03 x 1,5707 rad = 1,618
1 - 1,03 - 1,06 - 1,12 - 1,25 - 1,6 - 2 - 2,5 - 3,15 - 4 - 5 - 6,3 - 8 - 10
NJR (1,5707) = 1,253
6,283 rad / 5 = 1,256 rad
1 - 1,03 - 1,06 - 1,12 - 1,25 - 1,6 - 2 - 2,5 - 3,15 - 4 - 5 - 6,3 - 8 - 10
NJR (1,2533) = 1,12
1 - 1,03 - 1,06 - 1,12 - 1,25 - 1,6 - 2 - 2,5 - 3,15 - 4 - 5 - 6,3 - 8 - 10
NJR (1,12) = 1,06
1 - 1,03 - 1,06 - 1,12 - 1,25 - 1,6 - 2 - 2,5 - 3,15 - 4 - 5 - 6,3 - 8 - 10
NJR (1,06) = 1,03
1 - 1,03 - 1,06 - 1,12 - 1,25 - 1,6 - 2 - 2,5 - 3,15 -4 - 5 - 6,3 - 8 - 10
NJR = neliöjuuri
Edellä esitetty on näkemisen geometriaa ja laskelmia, ilman nähtäviä kuvioita. Emmehän näe ilmiöitäkään, vaikka ne varmuudella ovat olemassa. Ilmiöiden seuraukset sen sijaan tunnemme hyvin. Ne omaavat monessa tapauksessa yllä olevan muodon tavalla tai toisella. Miksi sivun otsikon nimenä on "numero viisi", vaikka sitä ei esiinny sivulla. Syynä on se, että yritän kertoa tällä sivulla, ettei kaikki ole nähtävää. Voisin kertoa viidestä sormesta, jolla avasitte tietokoneen. Viidestä sormesta, johon tukkimiehen kirjanpito perustuu ja jatkaa tämän sivun ainoaan kuvioon, viisikulmioon. (125)
26. Viisi peruslaskutapaa
Samaa tarkoittava suhdelaskenta tarvitsee näistä neljä peruslaskutapaa.
Yhteenlasku Vähennyslasku
1 + 1= 2 2 - 1 = 1
Kertolasku  Jakolasku Jakolasku
1 x 2 = 2 2 / 1 = 2
Modulaariset luvut
Peruslaskutoimitukset ovat tunnettuja. Modulaariset luvut ovat useille tunnistamaton käsite. Modulaariset luvut kuuluvat matematiikan eriskummallisimpiin ja ihmeellisimpiin olioihin. Ne ovat kuitenkin matematiikan syvällisimpiä käsitteitä. 1900-luvun matemaatikko Martin Eichler pitää modulaarisia muotoja yhtenä viidestä peruslaskutoimituksesta. Muut ovat yhteen-, vähennys-, jako- ja kertolasku. Usea matemaatikko hallitsee neljä peruslaskutoimitusta, mutta viidennen sanotaan tuottavan vaikeuksia. Modulaaristen muotojen keskeinen piirre on niiden symmetrian suunnaton moninaisuus. Kappale on symmetrinen, jos sitä voidaan muuntaa tietyllä tavalla niin, että se näyttää jälkeenpäin muuttumattomalta. Modulaarista muotoa on mahdotonta piirtää tai edes kuvitella. Taniyaman ja Shimuran tutkimia modulaarisia muotoja voidaan siirtää, kääntää, vaihtaa keskenään, peilata ja kiertää äärettömän monella tavalla. Silti niiden säilyessä muuttumattomina. (11)
27. Viisi tapaa käsitellä muutosta
Luku viisi on tärkeä samaa tarkoittavassa suhdelaskennassa. Esimerkiksi Pascalin kolmiossa havaitsemme viisi laskettavaa riviä. (81)
Funktiot ja luvut
Matemaattinen analyysi Vektorilaskenta
Kaaosteoria  Differentiaaliyhtälöt Differentiaaliyhtälöt
Dynaamiset järjestelmät
Kuva Wikipedia, jossa saatavana tietoa laskentatavoista
28. Samaa tarkoittava suhdelaskenta
Suhdelaskennan menettelyllä on mahdollista laskea tunnettua asioista ja tämän lisäksi rinnakkaista tietoa ilmiöistä. Maanpäälliset ilmiöt liittyvät painovoimaan ja valon nopeuteen. Toisella tavalla asioita tarkastelemalla matematiikka on tajunnan valoa, josta laskennan myötä syntyy laskennallinen varjo. Näistä laskennan tuloksista eli käsitteellisistä varjoista näkee asioita, jotka kirkas valo peittää näkyvistä. Vastaava tapahtuma on valokuvattaessa filmikameralla, jolloin valokuvan tummista kohdista, ei pysty erottamaan yksityiskohtia. Kuvaa kehitettäessä on mahdollista lisävalottaa tummia kohtia ja näin saada yksityiskohtia kuvaan näkyviin. Periaate kuvaa kehitettäessä on, alivalottuneesta negatiivista saa aikaiseksi kohtalaisen valokuvan, ylivalottuneesta tämän onnistumatta samassa määrin. Me, jotka olemme kehittäneet valokuvia, tunnemme ilmiön.

Suhdelaskenta on rinnakkainen asioiden ja arvojen tarkastelutapa, josta on siirtyminen varjojen maailmaan. Tätä kuvaa Platonin luolaesimerkki varjoista, josta luette fysiikan ensimmäisellä sivulla. Olette tämänkin jälkeen nimekkäässä ja luotettavassa seurassa tutustuassanne suhdelaskentaan. Hahmotamme asioita erilaisten kuvioiden avulla, olemalla tulosten kannalta siinä, missä perinteisellä laskentakaavalla olisimme. Suhdelaskennassa ei opiskella kaavoja, vaan hahmotetaan kokonaisuutta tarkastelulla, joka on tuhansia vuosia vanha ajatus. Tässä ajassa toteutettu laskenta on kuvaus materiasta, tuotteen arvojen muodostuksesta, sekä ilmiöistä. Sivut muotoutuvat sisällön ja sijainnin osalta muutosprosessina. Kuvaavaa sivuille on, niiden olevan kuin lasten leikkipalikoita, niiden liittyessä saumattomasti rakennelmasta toiseen.
Muusta laskemisesta poiketen, suhdelaskentaan tutustumisen voi aloittaa haluamastaan kohdasta, tämän sotkematta kokonaiskuvan muodostumista. Suhdelaskenta rakennelmana ei valmistu koskaan, tämän merkitsemättä enempää, kuin muun tiedon yhteydessä. Emme tule tietämään lopullisesti mitään. Tästä siirrymme samaa tarkoittavaan suhdelaskentaan, joka muodostuu useasta erilaisesta matematiikasta tai paremmin sanoen ilmiöiden tarkastelusta.
Näkemisen geometria
Kuinka geometriset kuviot sisältävät ilmiöiden rakenteen.
Fysiikka
Ilmiöt saavat rinnakkaisen tarkastelutavan
Lujuuden määrittely
Lujuuslaskennassa rauta käyttäytyy ilmiöiden kaltaisesti
Fysiologia
Fyysinen ja fysiologinen ilmiö ovat samasta eli alkuräjähdyksestä, liittyen painovoimaan.
Historia
Laskennan aihepiiriin kuuluu myös laatu ja sen laskeminen.
Tuotteet
Tuotteet saavat myös osansa teknisenä selostamisena ja laskentana.
Virtuaalinen yritys
Tuotteiden lisäksi on myytävänä virtuaalinen yritys lukuisine tuotteineen. Viimeisenä, mutta suinkaan merkityksettömimpänä on historia. jota ilman emme olisi tässä. Historia on erillinen osuutensa, samoin sitä on ripoteltu sivujen yhteyteen.
Mikä tahansa sivu liittyy osittain tai kokonaan toiseen sivuun, sillä laskenta on matemaattinen rakennelma.
29. Suhdelaskenta ja näkemisen geometria
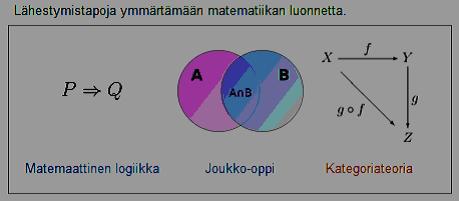
Samaa tarkoittava suhdelaskenta on lähestymistapa ymmärtää maailman rakenne, merkityksessä koskettaen arkipäivän elämää. On hätkähdyttävää lukea kolmesta lähestymistavasta ja havaita kirjoittavani kahdesta viisikulmiosta puuttuvasta laskennan menettelystä. Koska nämä ovat sivuni, voin näin kirjoittaa. Ymmärrän ajatuksena neljä viidestä lähestymistavasta, kategoriateorian avautumatta. Tämän tarkoittamatta, että laskennalla ei olisi paikkaa muiden rinnalla. (341)
Suhdelaskenta Näkemisen geometria
Joukko-oppi  Kategoriateoria Kategoriateoria
Matemaattinen logiikka
Kuva alla Wikipedia, josta saatavana lisätietoa laskentatavoista
30. Suhteellisuuden syntyminen
 Ennen alkuräjähdystä ei ole aikaa, tai paikkaa tapahtumalle. Kaikki materia on tiivistyneenä pisteeseen, jonka suuruus on elektronia pienempi. Piste räjähti. Mitä tapahtui tämän jälkeen, on tiede kyennyt kuvaamaan tarkasti tähän päivään. Samalla syntyi 20/80 sääntö, jota kuvaa viisikulmio. Viidestä tapahtumasta yksi vastaa 80 % tapahtumien yhteisvaikutusta. Ennen alkuräjähdystä ei ole aikaa, tai paikkaa tapahtumalle. Kaikki materia on tiivistyneenä pisteeseen, jonka suuruus on elektronia pienempi. Piste räjähti. Mitä tapahtui tämän jälkeen, on tiede kyennyt kuvaamaan tarkasti tähän päivään. Samalla syntyi 20/80 sääntö, jota kuvaa viisikulmio. Viidestä tapahtumasta yksi vastaa 80 % tapahtumien yhteisvaikutusta.
Alkuräjähdyksessä syntyi vetyä ja heliumia. Muut alkuaineet puuttuivat, eikä elämää tai planeettoja synny edellä mainituista aineista. Usein ajatellaan tähtien välinen avaruus tyhjyydeksi, mutta tiede todistaa sen olevan harvaa ainetta. Välittömästi alkuräjähdyksen jälkeen syntyi 80 % vetyä ja 20 % heliumia. Nykyään avaruudessa on myös raskaampia alkuaineita ja molekyylejä etyylialkoholista aminohappoon.
Emme kyseenalaista lainalaisuutta 20/80 nyrkkisäännöstä. Säännön tarkoittaessa 20 % tapahtumia kattavan 80 % tapahtumista. Vasenkätisten määrä ihmisistä on n. 20 %.
80% yhtiön voitoista tekee 20% sen asiakkaista
80% yhtiön valituksista tekee 20% sen asiakkaista
80% yhtiön voitoista syntyy 20% henkilöstön käyttämästä työajasta
80% yrityksen myynnistä tekee 20% sen tuotteista
80% yhtiön myynnistä tekee 20% sen myyntihenkilöstöstä
80 % päivittäistavarakaupasta Suomessa hallitsee kaksi kauppaketjua
Suhdetta voi käyttää kuvaamaan myös ilmiöitä, joiden kuvaamiseen se ei sovi. (323)
41. Kemiallisten aineiden jaksollinen järjestelmä
 Alkuaikoina kemistit huomasivat, että aineita ei voi sotkea keskenään miten sattuu. Tietyt suhteet säilyivät aineita sekoitettaessa. Tämä oli todiste atomien puolesta. Atomipainoihin ei aluksi kiinnitetty huomiota, sillä näiden mittaaminen oli hankalaa. Atomipainoissa ei ensin ollut havaittavaa yhteneväisyyttä, kun havaintoja oli vasta kuudestakymmenestä alkuaineesta. Näytti, ettei atomipainolla ollut tekemistä aineen kemiallisen ominaisuuden kanssa. Venäläinen Dimitri Mendelejev (1834-1907) valmistui kemistiksi ja alkoi valtion palkkalistoilla luokitella öljyjä. Tässä työssä hänelle tuli mieleen luokitella aineet, alkuaineet mukaan lukien. Alkuaikoina kemistit huomasivat, että aineita ei voi sotkea keskenään miten sattuu. Tietyt suhteet säilyivät aineita sekoitettaessa. Tämä oli todiste atomien puolesta. Atomipainoihin ei aluksi kiinnitetty huomiota, sillä näiden mittaaminen oli hankalaa. Atomipainoissa ei ensin ollut havaittavaa yhteneväisyyttä, kun havaintoja oli vasta kuudestakymmenestä alkuaineesta. Näytti, ettei atomipainolla ollut tekemistä aineen kemiallisen ominaisuuden kanssa. Venäläinen Dimitri Mendelejev (1834-1907) valmistui kemistiksi ja alkoi valtion palkkalistoilla luokitella öljyjä. Tässä työssä hänelle tuli mieleen luokitella aineet, alkuaineet mukaan lukien.
Hän sijoitti aineet atomipainojen mukaan ja oletti osan alkuaineista olevan löytämättä ja osan punnituista atomipainoista vääriksi. Näin hän sai alkuaineet sijoittumaan säännön mukaisiin paikkoihin. Tämä tunnetaan alkuaineiden jaksollisena järjestelmänä. Samaa tarkoittava suhdelaskenta on paljossa samaa alkuaineiden jaksollisen järjestelmän kanssa. Jokaisella ilmiöllä ja vaikkapa tuotteella on oma paikkansa arvoavaruudessa. (92)
42. Kaikella on sijainti
42.1. Aakkoset
Aakkoset kuvaavat suhdelaskentaa, jossa on ajatus kuten kirjaimissa eli kaikilla on määritettävä paikkansa. Kutsuttaessa ihmisiä nimijärjestyksessä, voi suurin piirtein päätellä milloin on oma vuoro. Sen sijaan kirjaimet nimessä ovat tarkasti määrätyillä paikoilla, jolloin esimerkiksi nimet Laura ja Noora ovat tunnistettavissa kaikkialla maailmassa. Nooran nimestä voi silti jäädä tai tulla lisätyksi toinen o-kirjain. Aakkosissa jokaisella kirjaimella on tarkka, edeltä käsin määritetty paikka, jonka järjestyksen opettelemme ensimmäiseksi. Kirjaimet muodostavat nimet, asiat ja sanat. Sanat muodostavat lauseet, jotka selittävät meitä ympäröivän.
On luultavasti absurdi ajatus, muuta väittää tässä asiassa?
42.2. Kirjaimet
Vastaavalla tavalla kuin aakkoset, numerot ovat määritettävässä asemassa toistensa suhteen. Tiedetään numeron viisi olevan kahden kokonaisluvun päässä numerosta kolme, kuten myös numerosta seitsemän. Vastaava tilanne, on kaikilla muillakin numeroilla.
Tässäkin yhteydessä on luultavasti absurdia muuta väittää?
Samoin kuin kirjaimet muodostavat sanoja, numerot muodostavat lukuja. Esimerkiksi luku 585 muodostuu kolmesta numerosta, määrittäen tarkasti määrän. Numerot muodostavat vastaavan merkityksen laskelmissa, kuin kirjaimet sanoissa Esimerkkinä nimi (suurella varmuudella) ilmaisee sukupuolen. Toinen esimerkki on fysiikan tapa määrittää voima massan ja kiihtyvyyden avulla. Kolmantena yhteenlasku, jonka suuri osa maailman ihmisistä hallitsee.
Laura = tyttö (nainen)
F = m x a
3 + 4 = 7
42.3. Taivaankappaleet
Taivaankappaleilla on tarkasti määrätyt paikkansa ja niiden liikkeen synkroni määrittää ajan toistensa suhteen. Esimerkkinä kuunpimennysten ennustaminen tuhansia vuosia eteenpäin. Asia on tunnettu niin kauan, ettemme oikeastaan sitä enää tiedä.
42.4. Aikamääritteet
Sekunnit, minuutit, tunnit, päivät, kuukaudet ja vuodet ovat tunnetussa sijainnissa. Samoin vuodenajat tulevat järjestyksessä, kuten monet asiat tässä maailmassa.
42.5. Rautatieasemat
Matkustettaessa junalla, tulevat juna-asemat vastaan samassa järjestyksessä, jossa ne jäivät taakse. Kiertävää junarataa ei ole monessa paikassa. Silloinkin asemat ovat aina samassa järjestyksessä, joka mahdollistaa aikataulun junalle. Arvot ilmiöissä ovat kuin juna-asemia radan varrella, mahdollistaen arvon määrittämisen sen sijainnin etäisyyden perusteella.
Tilanne tänään
Osaamme laskea määriä, ilmiöitä jne. mielin määrin, mutta emme osaa sanoa muutosta ilmiössä sitä laskematta kaavoina. Entäpä kun ilmiöön ei ole olemassa yksiselitteistä laskentamallia? Samaa tarkoittava suhdelaskenta tulee tässä avuksi. Kuinka se on mahdollista? Juuri siten, kuten ymmärsitte edellisen lukemalla. Kaikella on paikkansa, joten arvollakin on paikkansa, josta se on vivuttavissa esiin. (750)

43. Suhdelukujono
1 - 1,25 - 1,6 - 2 - 2,5 - 3,15 - 4 - 5 - 6,3 - 8 - 10
1 - 1,008 - 1,015 - 1,03 - 1,06 - 1,1(2) - 1,25 - 1,6 - 2 - 2,5 - 3,15 - 4 - 5 - 6,3 - 8 - 10
1 x 1,25 = 1,25 1 x 1,008 = 1,008
1,25 x 1,25 x 1,03 = 1,618 1,008 x 1,008 = 1,015

0 - 0,25 - 0,6 - 0,2 - 0,25 - 0,315 - 0,4 - 0,5 - 0,63 - 0,8 - 1
1,6 x 2 = 3,15 2 x 1,008 = 1,015
2 x 2,5 = 5 2 x 1,015 = 1,03
2 x 3,15 = 6,3 1,015 x 1,015 = 1,03
4 x 1,6 = 6,3 2 x 1,03 = 1,06
1,6 x 6,3 = 10 1,03 x 1,03 = 1,06
8 x 2 = 16 ... jne. 2 x 1,06 = 1,12 ....etc.
1,618 on jotakin, joka poikkeaa. Muuten ajatus suhdelukujonosta on yksinkertainen. Ensimmäisellä kerralla ette ole uskoa kertomalla ja yhteenlaskemalla saatavan samaa. Pascalin kolmio viestittää vasemmalta (yhteenlasku) ja oikealta (kertominen) olevan saman. Symmetria tarkoittaa, että vasen kätesi on oikea kätesi. Laita kädet yhteen ja näet sen. (275)
2 + 2 = 4 jolloin toteatte 2 x 2 = 4
Pascalin kolmion symmetria
==> <==
1 1 1
1,1 1 1 1,1
1,21 1 2 1 1,21
1,331 1 3 3 1 1,331
44. Suhdelukujen yhteen- ja kertolasku
1 - 1,008 - 1,0015 - 1,03 - 1,06 - 1,12 - 1,25 - 1,6 - 2,0 - 2,5 - 3,15 - 4 - 5
1,0082 = 1,015 1,008 pyöristetty arvosta 1,0075
=> 1,0152 = 1,03
=> 1,032 = 1,06
=> 1,062 = 1,12
=> 1,122 = 1,25
=> 1,252 = 1,57
=> 1,57 x 1,03 = 1,618
Kertoimen voi kertoa itsellään tai laskea yhteenlaskuna
1,015 + 0,015 = 1,03 tai 1,015 x 1,015 = 1,03 Staattisen väsymisen kerroin
1,03 + 0,03 = 1,06 or 1,03 x 1,03 = 1,06
1,06 + 0,06 = 1,12 tai 1,06 x 1,06 = 1,12 Pascalin kolmion rivikerroin 1,1(2)
1,12 + 0,12 = 1,25 or 1,12 x 1,12 = 1,25 Yleinen vanhenemiskerroin
Epäsymmetrisyys syntyy kertoimen 1,25 jälkeen, joka liittyy laskentaan liittyvään lukuun 5. Lukuun viisi saakka arvot ja ilmiöt ovat suoraan määritettäviä, tämän jälkeen niiden hämärtyessä, ilman soveltuvaa tarkastelumenettelyä. Luku viisi on laskennan perusarvo. Historiasta voimme lukea, kuinka luvun viisi merkitys on tunnettu ennen suhdelaskentaa. Esimerkkinä vaikkapa tässä yhteydessä Pythagoras.
1,25 x 1,25 = 1,57
1,57 x 1,03 = 1,618.
1,618 x 1,618 = 2,618
1,618 + 1 = 2,618
Suhdelaskenta ei ole desimaaleja, vaan kokonaisuuden hahmottamista. Sijoittamalla lukuja laskukoneeseen, tulos ei ole desimaalilleen se, mitä yllä olen kertoimien arvoksi määrittänyt. Kokonaisuuden hahmottamisen jälkeen, suhdeluvut ovat suuren tarkkuuden muodostavia laskentaan, sillä suhdeluvut kompensoivat niiden sisäiset virheet. Pinontavaunun esimerkin yhteydessä 48 gramman tarkkuus konekilven antamaan informaatioon nähden on satoja laskelmia ja testejä sisältävä. Lopulta emme tiedä, oliko lähtökohtana oleva pinontavaunu oikein mitoitettu, sillä laskenta ei anna siihen vastausta. Lähtökohta kuitenkin on kaikkein kokeneimpien yritysten pystyvän suunnittelemaan oikein mitoitettuja tuotteita. (71)
45. Eri mittayksiköt
Metrisen ja tuumallisen maailman suhde yhdistyy kultaisen leikkauksen suhteeseen 1,618. Onnekkaasti ja samalla selitettävästi tämä tekee näiden kahden maailman laskemisesta samaa tarkoittavaa. Pituusmitta metri ei ole sattuma, josta päästään tuuman pituuteen. Hyvin harvalle tätä on selvitetty, joka tulee sivuillani vuorollaan selvitetyksi. Ensin on hyvä tarkistella visuaalisesti metrin, kilometrin, malin ja tuuman keskinäistä suhdetta.
1,0 - 1,25 - 1,6 - 2,0 - 2,5 - 31,15 - 4,0 - 5,0 - 6.3 - 8,0 - 10,0
1 m - 1,618 km 1000 m
1 cm - 1 tuuma = 2,5 cm
1 Tuuma - Maili = 63.700 x 1 tuuma
Kerroin kerran lujuuslaskennan menettelystäni eräälle insinöörille, hänen sanottuaan olevansa erikoistunut lujuuslaskentaan. Laskelmia katsottuaan hän sanoi; "laskelmat eivät ole mm mitoituksella. Meille on opetettu, että laskenta tehdään millimetreissä, eikä hän hallitse muita yksikköjä". Menin sanattomaksi väitteestä, pahoitellen niiden ihmisten puolesta, jotka eivät tätä tiedä käyttäessään tuumia, nauloja jne. Voin kuvitella olevani muinaisessa Roomassa esittelemässä arabialaisia numeroita ja erikoisesti numero nollaa, joka heiltä puuttui. Vastaväitteenä olisi saattanut olla, ettei tyhjä tarvitse merkkiä. Roomalaiset kylläkin osasivat jättää laskelmissa tyhjän paikan nollan vastineena. Toisena väitteenä olisi voinut olla, että kirjanpidossa nolla oli helppo väärentää numero kuutoseksi tai yhdeksäksi, mutta roomalaisilla numeroilla näin ei ainakaan helposti voisi tehdä jne. Mikä on teidän vastaväitteenne suhdelaskentaa vastaan:)
Laskenta lähtee ajatuksesta, jossa suure voi olla käyttäjän mieltämä, mutta mielellään SI-järjestelmän mukainen. Näitä voi laskea keskenään, niiden muuttamatta lopputulosta. Tämän ymmärtäminen voi olla vaikeaa, mutta eri mittayksiköiden käyttö, on ymmärrettävää maailmassa. Ajatellaan kultaisen leikkauksen suhdelukua 1,618, kilometrin pituutta 1000 m ja mailin pituutta 1609 m. Laskennassa mailin ja kilometrin välille, syntyy 9 metrin virhe, joka vaikuttaa luvun kolmanteen desimaaliin. Tuuman pituudella 25 mm on laskennan kertoimen 2,5 vastaavuus. Tästä jatkamalla tuuma on 63700 osa mailista eli kertoimen 6,3 mukainen. Eri suureet eivät välttämättä aiheuta ongelmaa, joten voi osittain sotkea yksiköitä keskenään. Laskenta pysyy kuitenkin SI-järjestelmässä. (56)
46. Suhteellisuuden kuvaaminen kuvioiden kautta
 Suhteellisuus on kuvattavissa kuvioilla. Viisikulmio on ansaan näköinen yläosaltaan. Piirrettäessä säännöllinen viisikulmio, kuten kuvassa ja määritettäessä ansaan vinot paarteet 100 cm pitkäksi => Vaakaviiva on 100 x 1,618 cm, on 1,618 m. Näin määrittyi kultaisen leikkauksen mittasuhde. 2 x 100 cm / 161,8 cm = 123,6 cm => suhde 100 /123,6 = 0,8. Viisikulmio kuvaa yksinkertaisen suhteellisuuden tapahtumissa ja ilmiöissä. Suhteellisuus on kuvattavissa kuvioilla. Viisikulmio on ansaan näköinen yläosaltaan. Piirrettäessä säännöllinen viisikulmio, kuten kuvassa ja määritettäessä ansaan vinot paarteet 100 cm pitkäksi => Vaakaviiva on 100 x 1,618 cm, on 1,618 m. Näin määrittyi kultaisen leikkauksen mittasuhde. 2 x 100 cm / 161,8 cm = 123,6 cm => suhde 100 /123,6 = 0,8. Viisikulmio kuvaa yksinkertaisen suhteellisuuden tapahtumissa ja ilmiöissä.
Viisikulmio on todennäköisesti tärkein suhteellisuutta kuvaava kuvio. Samaa kuvaavat myös ellipsi, ympyrä ja pyramidi. Tieteen mukaan pyramidiin ei liity muuta kuin mielikuvitusta. Tässä tapauksessa, laskimemme osoittaa siinä tapauksessa rikkaan mielikuvituksen. (714)
161,8 cm / 2 = 80,9 cm
arc coa 80,9 cm / 100 cm = 36
36 / 360 = 0,1
1 + 0,1 = 1,1
=>
47. Matemaattinen olio
Natematiikan filosofia on filosofian osa-alue, joka tutkii matematiikan filosofisia perusteita, oletuksia ja seurauksia.

Perinteisesti on ajateltu, että metafysiikka pyrkii pääsemään pelkkien ihmisille ilmenevien seikkojen, havaintojen ja harhojen ”taakse” ja kertomaan perimmäisen totuuden asioista.
Kuinka vanha ajatus matemaattisista olioista on, ei varmuudella tiedetä. Tiedämme länsimaisen filosofian juurien johtavan Platoniin. Seuraavana Wikipedian kuvaus Platonista; Platon oli tyyliltään kaunokirjailija, joten hänen kirjoituksensa sisälsivät tarinoita, vertauskuvia ja myyttejä yhdistettynä käsitteiden tutkimiseen. Platonin luolavertaus on tunnettu ja johon voi tutustua suhdelaskennan fysiikassa. Platon tutki metafysiikkaa, mutta mitä metafysiikka on? Aristoteles kirjoitti metafysiikan rinnalla fysiikasta, joista kirjoista käytetään yhteisnimitystä fysiikka. Aristoteleen teoksia järjestäneet oppineet ensimmäisella vuosisadalla Aleksandriassa alkoivat nimittää näitä kirjoja nimellä τα μετα τα φυσικά (ta meta ta fysika) eli "(kirjat) jotka tulevat fysiikan (kirjojen) jälkeen".
Termiä ontologia käytetään useassa merkityksessä. Termiä käytetään myös puhuttaessa tietyn metafyysisen teorian tai järjestelmän olettamasta olioiden joukosta. Samaa tarkoittavan suhdelaskennan näkökulmasta geometriset kuviot mm. viisikulmio piirroksena ja Pascalin kolmio ovat matemaattisia olioita. Näihin sisältyy kuvaus maailman ilmiöistä arvojen muodostajana.
Ontologia tutkii olemisen ja olemassaolon käsitteitä ja olevaisen perimmäistä laatua. Samaa tarkoittava suhdelaskenta puolestaan tarkastelee ilmiöiden välisten suhteiden luonnetta. Matemaattiset kaavat ovat subjektiivinen tarkastelu ilmiöiden osa-alueista. Suhdelaskenta sen sijaan on kokonaisvaltaisempi kuvaus (oletetusta) olevaisesta itsestään. Näin tarkastelluista ilmiöistä tulee samaa tarkoittavia, mahdollistaen tarkastelun useasta ilmiöstä. Samaa tarkoittavaa suhdelaskentaa ei olisi, jos muilla menettelyillä tämä olisi ollut mahdollista.
Aikanaan kreikkalaiset ajattelivat, ettei numero 1 ole luku, vaan paremminkin pituuden yksikkö. Suhdelaskennan kannalta tämä on mielenkiintoinen päätelmä, sillä luku 1 on mikä tahansa pienin tunnettu arvo tarkasteltavasta. Esimerkiksi 100 m juoksu on lyhyin kilpailtava juoksumatka, merkiten laskennassa arvoa 1, johon muita juostavia matkoja Maratonin matkaan saakka verrataan. Suhdelaskennan ajatteluna ihmiset eivät tee matemaattista keksimistä. Löydämme ainoastaan asioita joita ovat esimerkiksi ympyrä ja kolmio. (683)
48. Domino vaikutus
Ketjureaktio ilmenee, kun pienikin muutos aiheuttaa vastaavan kaltaisen muutoksen läheisyydessä. Tämä tapahtuu lineaarisessa järjestyksessä kuten viivan pisteet. Varjot alla olevassa kuvassa esittävät saman kuin palikat. Mikäli ensimmäinen dominopalikka kaatuu, tiedämme viimeisen palikankin kaatuvan kuvan tapauksessa. Laskettaessa tiedämme arvon jostakin, jolloin tiedämme arvon toisista, jotka ovat samalla käyrällä. Edellä oleva tarkoittaa vastaavien tapauksien löytyvän yhteiseltä käyrältä. Ilmiöt ja tuotteet kuuluvat niiden omille käyrille. Edes asioiden oleminen samalla käyrällä, ei ole välttämätöntä, mutta siitä myöhemmin. Valokuvassa dominopalikat muodostavat esimerkin käyrästä.

Kerrottu Platonin luolavertaus muodostui konkreettisista todellisuuden varjoista, mutta varjoja on monessa muodossa. Kuormapalkin ollessa kuormitettu, sen varjo on mitattavaa taipumaa. Varjo eli taipuma kertoo tarvittavan palkista. Kilpajuoksun yhteydessä, varjo on aikaa, jolloin käytetty aika kertoo tarvittavan tapahtumasta.
Laskenta on enemmän kiinnostunut fysiikasta ja tuotteiden muodostumisesta, joskaan mikään inhimillinen ei jää ulkopuolelle. Seuraava on esimerkki käyrästä, jollaisen tuotteet ja ilmiöt esittävät niiden arvoina. (810)

49. Pascalin kolmion kerroin 11
Matematiikassa Pascalin kolmion rivien välinen kerroin on 11. Samaa tarkoittavassa suhdelaskennassa 1,1, jolloin seuraava osoittaa kertoimen 11 arvon.
Pascalin kolmio
1 dim 1 = 1 1 = 1
2 dim 1 1 = 1 +1 = 2 1,1 x 1 = 1,1
3 dim 1 2 1 1,1 x 1,1 = 1,21
4 dim 1 3 3 1 = 8 1,1 x 1,21 = 1,331
5 dim 1 4 6 4 1 1,1 x 1,31 = 14641
Neljännen ulotteisuuden kerroin on 1,331


Deflection
Kuorman kasvaessa kaksinkertaiseksi, kokonaisuuden muutos ksavaa 11 kertaiseksi. Kuorman aiheuttama taipuma kasvaa kahdeksan kertaiseksi, kun jänneväli kasvaa kaksi kertaa suuremmaksi. Sen osoittaa 4 dim rivin yhteenlasku.
Se mitä ei näe, on staattisen väsymisen kerroin; 1,331 x 8 x 1,03(28) = 11
Aikadilaatio taulukko
Jännevälin kasvaminen on yksiulotteista etenemää, jonka kerroin on 1,25. Aivan samoin kuin avaruusaluksen eteneminen avaruudesta 75000 km/s, johtaen aikadilaatioon. Aikadilaatiossa valon nopeudella 0,25, "kitka" on suuruudeltaan 1,03(28). Sen voi todeta taulukosta. Etenemiseen kolmeulotteisessa maailmassa, neljäs ulotteisuus tuo kertoimensa.
1,253 x 1,03 = 2

Liikkuvien kappaleiden aikadilaatio (Eng)

Profile L1000 σt Ix Wx Iy Wy Area
Nimike cm kN/cm2 cm4 cm3 cm4 cm3 kg/m A cm2
HEB100 518 2,2 450 90 167 33,5 20,4 26
Taulukko: Kun jänneväli 519 (518) cm => taipuma on 0,518 cm
Taipuma kannattajan painosta;
Kannattimen paino
10,36 m x 20,4 kg/m = 2,08 kN
f = taipuma / deflection
f = 5 x F x L3 / 384 x E x I
f = 3,279 cm
Pistekuormasta aiheutuva taipuma;
F = 1 kN
f = F x L3 / 48 x I x E
f = 2,499 cm
Taipuma yhteensä;
3,279 cm + 3,251 cm = 5,800 cm
5,800 cm / 518 cm = 11,2
1 - 1,12 -1,25
11,2
112
(kerroin 1,12)
Laskenta ei ole desimaalien asettamista
(766)
50. Eksponentiaalinen arvokäyrä
Dominopalikoiden kaatuminen osoittaa eksponentiaalisen arvokäyrän, jota useat ilmiöt noudattavat. Kaksi pienintä arvoa käyrällä, ovat kaksi ensimmäistä palikkaa. Valokuvasta näkee palikoiden olevan vaakasuorassa, kuvaten suoraa viivaa 1 + 1 = 2. Seuraavat palikat eivät enää ole tällä suoralla. Tuotteen tai ilmiön arvon edustaessa pistettä käyrällä. Kahden ensimmäisen pienimmän pisteen välille kokonaisuutta, piirtyy suora viiva. Tämän määrittää Fibonaccin lukujono 1 - 1 - 2.
Väli palikoissa, kuvaa arvokäyrän pisteiden etäisyyttä. Mikäli väli on liian pieni, palikat eivät kaadu. Liian suuri väli, ne eivät ylety toisiinsa. Pienin kokonaisuus, on palikan koko. Dominopalikoiden sijainti määrittää käyrän muodon, niiden kaatuessa toinen toistensa päälle. Suhdelaskenta on saman kaltainen paikkasidonnainen laskennan menetelmä. (787)
61. Kultainen leikkaus
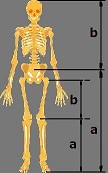 Jakamaton kokonaisuus suhteutuu suurempaan osaan samassa suhteessa, kuin tämä suhteutuu pienempään jaettuun osaan. Kultainen leikkaus on irrationaalinen vakio 1.61803398874989. Filosofiassa rationaalinen merkitsee järjen käyttöä päätöksentekoon ja irrationalisuus vastakohtaa. Jakamaton kokonaisuus suhteutuu suurempaan osaan samassa suhteessa, kuin tämä suhteutuu pienempään jaettuun osaan. Kultainen leikkaus on irrationaalinen vakio 1.61803398874989. Filosofiassa rationaalinen merkitsee järjen käyttöä päätöksentekoon ja irrationalisuus vastakohtaa.
Muita nimityksiä suhteelle ovat kultainen jako ja suhde. Laskennassa kultaisesta leikkauksesta käytetään kreikkalaista pientä kirjainta fii φ.

Golden ratio
a) Kantapäästä polveen - Kantapäästä napaan -
b) Polvesta lonkkaniveleen - Navasta pään päälle
( a + b ) / a = a / b = (fii) = 1,618 033 988
5 / 3 /1,03 = 1,618 5 > Laskennan suhteellisuusraja < 5 8 / 5 = 1,6
Kaikilla elävillä ja koneiden elimillä on tämä suhde.
Toisin sanoen
Katkaise tanko 100 cm kahteen osaan siten, että pitempi osa on 61,8 cm. Tanko on leikattu kultaisen leikkauksen suhteessa 100 cm /61,8 cm = 1,618.
Lyhyemmän osan pituus on 38.2 cm. Kultainen leikkaus antaa nimityksenä väärän mielikuvan, kuin leikkaaminen tietyssä suhteessa. Kultainen leikkaus on materiaan liittyvä kerroin, määrittäen voimien keskinäistä suhdetta. Vaarallinen leikkaus on käsite, jonka mallintamiseen voi käyttää alla olevaa piirrosta.
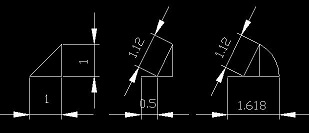
Kultainen leikkaus näkemisen geometriana
Pascalin kolmion rivien välinen kerroin 1,1, sekä lujuuslaskennan kerroin 1,12. "Katkaiseminen" voi jatkua viisi kertaa, jonka jälkeen suhteellisuusraja ylittyy. Saman voi kokeilla taittamalla paperin siististi viisi kertaa. (21)
62. Kultainen leikkaus tänään
Kultaiseen leikkaukseen on suositeltavaa tutustua Internetin välityksellä. Suuri osa avautuvista sivuista liittyy taiteelliseen sommitteluun, eräiden sivujen lähestyessä aihetta luonnon esimerkkien kautta, joita löytyy lukuisa määrä. Lopulta kaikki liittyy tavalla tai toisella kultaiseen leikkaukseen. Myöhemmin suhdelaskenta valottaa laskentaa kasveissa, vanhenemista väsymisen eri muodoissa jne. Seuraavan kerran matkustaessamme pyramideja katsomaan, tulemme tarkastelemaan niitä toisissa mietteissä. Nehän ovat aikansa tuotteita.

Internetin sivuilla suhdeluvun 1,618 merkitys iskostuu mieleemme. Joillakin sivuilla on kyse kaupallisuudesta, liittyen tuotteissa kultaisen leikkauksen suhteeseen 1,618. Arkkitehtuuri saa myös huomionsa valmistettujen rakennelmien kautta, alkaen Egyptin pyramideista ja jatkuen kreikkalaisen rakentamisen kautta tämän päivän tilakäsitteeseen. Silmissä kultaisen leikkauksen suhdeluvun mukainen rakennelma on sopusuhtainen, samalla todennäköisesti oikein mitoitettu. Tulen valottamaan tätä lujuuden määrittämisen yhteydessä materiassa ja tuotteissa. Internetin aineistosta saisi kirjan aikaan, annin jäädessä pintaraapaisuksi. Kultaisen leikkauksen matematiikasta on tehty maassamme vähintään kaksi yliopistollista lopputyötä. Nämä eivät muiden vastaavien lopputöiden tavoin ratkaise kultaisen leikkauksen merkitystä. Lopputyön tarkoitus, ei ole ratkaista tätä salaisuudeksi jäänyttä merkitystä. Kultainen leikkaus on kiehtonut ihmiskuntaa tuhansia vuosia. Kun siihen on tutustunut, aihe on pudottanut tarkastelijan kyydistä. Tätä samaa tarkoittava suhdelaskenta ei tee. (387)
63. Kultainen leikkaus kirjallisuudessa
Kultaisesta leikkauksesta ei ole kirjoitettu suomenkielistä kirjaa. Hakusana englannin kielellä, ei muuta tilannetta sanoilla Golden Mean, Golden Section jne. Lukusuhde on edelleen avoinna, kuten tuhansia vuosia tätä ennen. Kirjastonhoitaja ehdotti Encyclopedia Britannica tietosanakirjaa. Kirjasta ei löydy artikkelia aiheesta kultainen leikkaus. Kirjassa on sen sijaan runsaasti viittauksia artikkeleihin, joissa mainitaan kultainen leikkaus. Kirjan painos tosin yllätti tuoreudellaan. Maakuntakirjastossa sanahaku - kultainen leikkaus - kirjaston avustajan kanssa tuo kourallisen esimerkkejä lähinnä aikakausilehdistä.
 Lyijykynä kuvassa ei ole katkennut kultaisen leikkauksen suhteessa. Kultainen leikkaus murtumakohdassa on mukana ja selitetään aluksi ihmisen luiden kautta ja myöhemmin raudan eli teräksen lujuutena. Saamme tietoa lukusuhteesta, liittyen tekniseen suunnitteluun ja käsitteellisiin arvoihin. Sana kultainen leikkaus, antaa yksiselitteisen kuvan suomen kielellä ilmaisten. Yleisesti sana vastaa englannin kielen Golden Section merkitystä. Verratessa sanaa englannin kieleen, saamme kolme poikkeavaa merkitystä. Lyijykynä kuvassa ei ole katkennut kultaisen leikkauksen suhteessa. Kultainen leikkaus murtumakohdassa on mukana ja selitetään aluksi ihmisen luiden kautta ja myöhemmin raudan eli teräksen lujuutena. Saamme tietoa lukusuhteesta, liittyen tekniseen suunnitteluun ja käsitteellisiin arvoihin. Sana kultainen leikkaus, antaa yksiselitteisen kuvan suomen kielellä ilmaisten. Yleisesti sana vastaa englannin kielen Golden Section merkitystä. Verratessa sanaa englannin kieleen, saamme kolme poikkeavaa merkitystä.
Golden Mean
Ymmärretään filosofian kautta.
Golden Section
Janan jakaminen kultaisen leikkauksen mittasuhteessa 8:5.
Golden Ratio
Asioiden tarkasteleminen lukusuhteen 1,618 kautta kokonaisuutena.
Luemme kultaisesta leikkauksesta historiassa. Nautimme historian henkilöiden loistavasta ajattelun taidosta, joilla on samaa tarkoittavuus laskennan kanssa. Hämmästymme heidän ajattelunsa kaukonäköisyydestä. Tämän jälkeen laskemme esimerkkejä kuolevaisesta ja kuolemattomasta. Lopulta esitys muodostaa kattavan kokonaisuuden, jota ei ole aikaisemmin esitetty. Lähes kaikki laskenta tapahtuu tavalla, joka poikkeaa meille opetetetusta. Se mitä on opetettu, ei ole muodostanut yhtenäistä tarkastelua ilmiöiden kesken. Esittely ei ole historiaa, vaan tätä päivää ja tulevaisuutta. Kommentit asioiden yhteydessä, liittyvät suhteellisuuteen, johdattavat ympäröivän todellisuuden havaitsemiseen. Pythagoras, Albert Einstein. Johannes Kepler, Arkhimedes jne. (26)
64. Paperin taittaminen viisi kertaa
 Suhdelaskennassa luku viisi on tärkeä. Tee testi paperin taittamisesta. Puolita A4 -arkki mahdollisimman monta kertaa. Tämä taittamalla käsin ja taitoksen ollessa virheetön. Suhdelaskennassa luku viisi on tärkeä. Tee testi paperin taittamisesta. Puolita A4 -arkki mahdollisimman monta kertaa. Tämä taittamalla käsin ja taitoksen ollessa virheetön.
Suhdelaskennan mukaan 5 - 6 kertainen suhteellisuus on tarkasteltavaa. Saman virheellisyyden kasvamisen havaitsette paperin taitosten laadun huonontumisena. Ottaen käyttöön järeämmät välineet, kuin kädet, jopa kuusi taitosta voi onnistua. Samoin suhdelaskennassa on mahdollista tarkastella asioita, joiden suhteellinen asema tunnettuun, poikkeaa enemmän kuin 5 kertaa.
Ensin ajattelette voivan taittaa paperin lukuisan määrän. Näin ei ole todellisuudessa. Laskennasta nähdään taitossuhteitten olevan suhdelaskennan suhdelukuja vastaavat, jotka ovat suluissa.
1. 1 /2 = 0,5 (5,0)
2. 0,5 /2 = 0,25 (2,5)
3. 0,25 /2 = 0,125 (1,25)
4. 0,125 (/2) = 0,062 (0,63)
5. 0,062 /2 = 0,03125 (0,315)
Staattisen väsymisen kerroin 1,03 kaavasta E = m c2  on usein mainittu ja noudattaa asioissa ja arvoissa tapahtuvaa. on usein mainittu ja noudattaa asioissa ja arvoissa tapahtuvaa.
Pilkun edessä olevan ykkönen tunnettu ja kerroin esiintyy pilkun oikealla puolella.
Laskennan mukaan tunnettu kertaa tunnettu = tunnettu. Sama aritmetiikan mukaan 1 x 1 = 1.
Sen sijaan 1 x 1,03 = 1,03. Taittakaa paperi, niin ymmärrrätte tämän. (499)
65. Kilometrin ja mailin suhde
Joskus esitetään kysymys suhdelaskennasta ja sen tarkoituksesta. Ensimmäinen ajatus on sen olevan suhteellisuutta eri yksiköiden välillä. Otetaan aluksi kilometrin ja mailin välinen suhde, joka osoittautuu luonnon määrittämäksi kultaiseksi leikkaukseksi 1,618.
Kilometri on pituudeltaan 1 000 metriä. Tuuma on 2,54 cm => ( josta seuraa) jalka 12 tuumaa eli 30,48 cm => maili 5280 jalkaa = 1609 m. Suhdelaskennan kilometri ja maili ovat kultaisen leikkauksen kautta keskenään laskettavia. Pascalin kolmio määrittää viidennellä rivillä mailin pituudeksi 1611 m. Tuumamitoituksellinen maailma ja SI-järjestelmän mukainen maailma, voivat laskea suhdelaskennan menettelyllä yksikköjä keskenään. Näin ajatellen laskenta on yksiköitten välisten kertoimien tarkastelua. Liittämällä näkemisen geometrian mukaan kilometrin käsitteeseen, havaitsee Pascalin kolmion viidennen rivin muodostavan mailin pituuden kahden metrin tarkkuudella. Maailmaa ei ole niin tarkasti luotu, että sitä kannattaa monella desimaalilla laskea.
1 1 000 m (kilometri)
1 1 1,1 x 1,0 = 1 100 m
1 2 1 1,1 x 1,1 = 1 210 m
1 3 3 1 1,1 x 1,21 = 1 331 m
1 4 6 4 1 1,1 x 1,331 = 1 464 m
1 6 1 1 6 1 1,1 x 1,464 = 1 611 m (maili)
Ero Pascalin kolmion määrittämään mailin pituuteen on 2 m / 1 611 m x 100 = 0,12 %. Matka pituutena on yksiulotteista etenemää, joka väsyttää gravitaation kautta. Lopulta kaikki on samaa tarkoittavaa ja useassa tapauksessa keskenään vertailtavaa. Ensimmäinen rivi Pascalin kolmiossa on fysikaalisen maailman kerroin nolla-ulottuvuuteen. Viides eli alin rivi on suhteellisuuteen liittyvä kerroin. Kultaisen leikkauksen kerroin 1,618 liittyy kaikkeen luonnossa olevaan ja suureen määrään taidetta ja rakennelmia. Koneenrakennuksen lujuus, fysiikka ja fysiologia saavat osansa näistä tarkasteluista. (584)
66. Eri mittayksiköt 1
1,0 - 1,25 - 1,6 - 2,0 - 2,5 - 31,15 - 4,0 - 5,0 - 6.3 - 8,0 - 10,0
1 km - 1 maili = 1,618 km
1 cm - 1 tuuma = 2,5 cm
1 tuuma - 1 maili = 63700 x 1 tuuma
Erään kerran, kerroin laskennan menettelystä eräälle insinöörille. Hän sanoi olevansa erikoistunut lujuuslaskentaan. Laskelmiani katsottuaan hän sanoi; "laskelmat eivät ole mm mitoituksella. Meille on opetettu että, laskenta tulee tehdä millimetreissä, eikä hän hallitse muita yksikköjä". Menen sanattomaksi väitteestä, pahoitellen miljoonien ihmisten puolesta, jotka eivät tätä tiedä käyttäessä tuumia ja nauloja. Voin kuvitella olevani muinaisessa Roomassa esittelemässä arabialaisia numeroita ja erikoisesti numero nollaa, joka heiltä puuttuu. Tyhjän he kuitenkin osasivat jättää väliin.
Laskenta lähtee ajatuksesta, jossa suure voi olla käyttäjän mieltämä. Näitä voi laskea keskenään, niiden muuttamatta lopputulosta. Tämän ymmärtäminen voi olla vaikeaa, mutta eri mittayksiköiden käyttö, on ymmärrettävää maailmassa. Ajatellaan aluksi kultaisen leikkauksen suhdelukua 1,618, kilometrin pituutta 1000 m ja mailin pituutta 1609 m. Laskennassa mailin ja kilometrin välille, syntyy 9 metrin virhe, joka vaikuttaa luvun kolmanteen desimaaliin. Tuuma pituutena 25 mm on laskennan suhdeluku. Tästä jatkamalla tuuma on 63700 osa mailista eli suhdeluvun 6,3 mukainen. Eri suureet eivät aiheuta ongelmaa. Voimme laskea kuten aikaisemmin ja sotkea mittoja laskentaan. (56)
 Laskennan kannalta, mittasuhteet ovat usein yhteen laskettavia, ilman mittajärjestelmän muunnoksia. 20 mm ruuvi kertoimella 1,25 on 25 mm (käytännössä 24 mm), joka on tuuman halkaisijamitta. Laskennan kannalta, mittasuhteet ovat usein yhteen laskettavia, ilman mittajärjestelmän muunnoksia. 20 mm ruuvi kertoimella 1,25 on 25 mm (käytännössä 24 mm), joka on tuuman halkaisijamitta.
Tästä jatkaen eteenpäin kertoimella 1,25, putki 33,7 mm on 1" putki eli 1,25 x 25 mm = 31,25 mm. Laskennan kautta nämä kaksi mitoituksellista maailmaa lähentyvät toisiaan. Koska lujuudellinen mitoitus tehdään lopuksi, kohteen mitoituksen ja kuormitusolettamien varmistuttua, voidaan laskennat sekoittaa keskenään. Jos putken halkaisija ei riitä poikkileikkauspinta-alana, putken seinämän paksuutta lisätään. Seuraavaksi joutuisimme valitsemaan mitan 33,7 x 1,25 = 40 = 42 mm (putki tai ruuvi)
Poikkeavista komponenteista helpoimmin on saatavissa tuumamitoituksellisia tuotteita. Jatkoin tarkoituksella 25 mm ruuvista putkeksi, joita on saatavissa tuuma- ja metrisellä mitoituksella.
Putkissa alkuhankaluuksien jälkeen, ei ole vaikeutta. Kierteiden kohdalla on samoin ja ulkoapäin samankokoinen mutteri voi yllättää amerikkalaisessa ja japanilaisessa tuotteessa, olemalla muulla mitoituksella kuin oletimme. Itselleni kävi näin asennettuani pakoputken ja havaittuani puuttuvien muttereiden olevan UNF tai UNC -kierteellä varustetut. Arvaatte, oliko minulla sellaisia.
42 x 1,25 = 63 mm - 80 mm - 100 mm - 125 mm - 160 mm - 200 mm - 250 mm
erilaiset poikkileikkaukset materiaaleista ja komponenteista. (375)
67. Elävän ja kuolleen aineen suhdeluvut
67.1 Liike
1 - 1,008 - 1,0015 - 1,03 - 1,06 - 1,12 - 1,6
Pyörää pidetään ihmiskunnan tärkeimpänä keksintönä, joka kuvaa siirtyvää liikettä. Liikkeeseen liittyvät kertoimet 1 ... 1,618. Näkemisen geometriassa pyörää kuvaava muoto on ympyrä.
67.2 Staattinen liike
1,6 - 2,0 - 2,5 - 3,15 - 4 - 5
Paikallaan tapahtuvaa liikettä kuvaa keinutuolin jalat. Vastaava edestakainen liike syntyy aineessa, jolloin venyessään aine pitenee ja palautuu takaisin. Näkemisen geometriassa keinutuolin jalasta kuvaa ellipsi muotona.
1,25 x 1,25 = 1,57
1,57 x 1,03 = 1,618.
1,618 x 1,618 = 2,618
1,618 + 1 = 2,618
Suhdeluvut 1,618 ja 2,618 ovat merkityksellisiä materiaan liittyvänä. Voi ajatella elävän päättyvän suhdelukuun 1,25 väsymiseen liittyvänä tarkasteluna. Suhdeluku 1,618 muodostaa kulminaatiopisteen, jonka jälkeen siirrymme kuolleen - eli liikkumattoman aineen tarkasteluun. Suhdeluvun 2,618 myötä siirrymme elävään liittyvästä pyöreästä muodosta, elämätöntä kuvaavaan elliptiseen muotoon. Tiede toteaa, ettei kuollut materia eroa elävästä. Saman esittää laskennan esimerkit, laskiessa samalla menettelyllä rautakangen taipuman kuormitettuna ja ihmisen väsymisen urheilusuorituksessa.
67.3 Staattisen väsymisen kerroin
Kerroin 1,03 eli staattisen väsymisen kerroin, esitetään lukuisassa määrässä laskentaesimerkkejä. Kytkemme kertoimen arvon 1,03 gravitaatioon ja liikkeen pysäyttämiseen. Laskentaan liittyy käänteinen merkitys asioissa, jolloin kerroin myös jatkaa liikkeen määrää, joka havaitaan aikalaskelmissa. Liikkeen pysäyttämisen kaltainen ilmiö on väsyminen, joka jatkaa käytettyä aikaa. (754)


68. Havainnot
68.1 Havainto I
Tuotteen tai ilmiön arvon edustaessa pistettä käyrällä. Kahden ensimmäisen pienimmän pisteen välille kokonaisuutta, piirtyy suora viiva.
Kaksi pienintä arvoa voi määrittää yhteenlaskun periaatteella. Tästä eteenpäin näin ei menetellä, sillä arvot olisivat suoraan määritettäviä. Jotkut kirjat mainitsevat maailmankaikkeuden eksponentiaalisen rakenteen, sitä selittämättä, joten suhdelaskennalla on mainittu rakenne. Periaatteen suorasta viivasta merkitsi Fibonacci. (53)
Fibonaccin lukujono 1 - 1 - 2
1 + 1 = 2
68.2 Havainto II
Tuotteen tai arvon edustaessa pistettä. Kolmen tunnetun pisteen kautta voi piirtää käyrän.

Havainto I määritti kahden ensimmäisen arvopisteen välille muodostuvan suoran. Tästä eteenpäin arvolla on maailmankaikkeuden eksponentiaalinen kerroin.
Esimerkkinä nosto-orsien nostokorvien painot löytyvät matemaattiselta käyrältä, jossa paikka on määrätty tunnetun nostokorvan tiedon perusteella. Tunnettu arvo voi sijaita millä tahansa kohtaa käyrää. Siis ei välttämättä pienin arvo, määrittää arvot.
Kuvan 500 kg nostokorvake pienimpänä painaa 1 kg. Laskemalla 40 000 kg nostokorvake painaa 175 kg ja valmistettuna 170 kg. Korvakkeiden välinen painon ero on 170-kertainen, mutta laskennallinen ero vain 2,9 %.
Ilman suhdelaskentaa, painon määrittämiseen ei ole tunnettua menettelyä. Laskenta toimii vastaavalla tavalla myös käsitteellisiin arvoihin. Tarkasteltavan asian koolla tai kokoonpanolla ei ole tarkastelussa merkitystä, joten suhdelaskenta on erinomainen yksipuoliseen Benchmark tarkasteluun tuotteissa. (18)
68.3. Havainto III
Tuotekäsite
68.3.1. Tunnetun perusteella, muiden toimintaa vastaavien painot tunnetaan
68.3.2. Tunnetun perusteella, muiden toimintaa vastaavien hinta tunnetaan
- Ehdollinen väittämä
68.3.3. Tunnettu kapasiteetti määrittää muiden vastaavien kapasiteetit
68.3.4. Tunnetun ajan perusteella, muiden toimintaa vastaavien ajat tunnetaan
68.3.5. Tunnetun käsitteellisen arvon avulla, muut vastaavat tapaukset tunnetaan
Havainto III sisältää viisi kuvausta tuntemattoman selvittämiseksi. Monien mielestä havainnot ovat ristiriitaiset, mutta ovatko ne sitä? Käymme läpi lukuisan määrän tarkasteluja havaintoihin perustuen.
Tarkastelut kattavat kokonaisuuden kerrallaan, jolloin yksittäisten tarkasteluiden määrä kasvaa suureksi. Samaa tarkoittava suhdelaskenta on ainutlaatuinen Benchmarking työväline. Mikäli ette tunne benchmarking menettelyä, kerron siitä sivuillani. (19)
68.4 Havainto IV
Tuntemalla pienimmän, on suuri mahdollisuus tuntea suurempi. Pienimmän tuntemalla, seuraava määräytyy Fibonaccin lukujonoon perustuen. Mitkä asiat määräytyvät näin, kertoo laskenta. Ei ainoastaan pienintä seuravan, vaan kaikki tästä eteenpäin.
 Käsillä kosketeltavien arvojen ohessa, nämä liittyvät käsin koskettamattomiin arvoihin. Vaikkapa valmistettaessa halkaisija 160 mm kuljetinruuvi ja tiedettäessa kapasiteetti, tiedetään 400 ja 1000 mm kuljettimien kapasiteetit. Käsillä kosketeltavien arvojen ohessa, nämä liittyvät käsin koskettamattomiin arvoihin. Vaikkapa valmistettaessa halkaisija 160 mm kuljetinruuvi ja tiedettäessa kapasiteetti, tiedetään 400 ja 1000 mm kuljettimien kapasiteetit.
Voimme laskea hihna- ja ruuvikuljettimien kapasiteetteja, kun on olemassa varma tieto yhdestä tuotteesta.
Neuvolassa lapsi saa pituusennusteen aikuisena, kun tiedossa on pituus syntyessä ja vanhempien pituudet. (166)
"Pienin määrittää suurimman"
68.5 Havainto V
Käyrä määrittyy tunnetut pisteet käyrältä tuntemalla
 Edellytyksenä, tuotteesta tunnetaan arvot ja ulotteisuus. Edellytyksenä, tuotteesta tunnetaan arvot ja ulotteisuus.
Laskennan mukaan ulotteisuuksia on viisi. Leveys, pituus, korkeus, aika ja suhteellisuus.
Pituus ja aika => väsyminen
leveys ja korkeus => pinta-ala
leveys, korkeus ja pituus => tilavuus
Nostokorvat ovat esimerkkinä kuvaamassa käyrän muodostumisen tuotteessa. Vaastaava käyrä muodostuu yhtälailla aineettomasta ilmiöstä. (167)
68.6 Havainto VI
"Käyrän arvopisteiden joukko kuvaa abstrakteja ja konkreettisia arvoja".
Ajatus sisältyy havaintoon II, jossa tunnetun perusteella, toinen tunnetaan. Määritettävä voi olla laskennan apukerroin tai tuotteen arvo. Laskemme 1500 metrin juoksun ME -ajan 100 metrin ME ajan perusteella tai jonkin muun matkan ME-aikaan perustuen. Näin voimme käsitellä muitakin abstrakteja asioita. Yleensä laskemme pienemmän perusteella suuremman.
100 metrin ME-ajan perusteella laskettu 1500 m ME-aika, on tulos sekunnin sadasosien tarkkuudella. Tarkkuus kaikille juoksumatkoille on 1-1,5 %. Suhdelaskennassa ei ole kyse vain juoksumatkoista, vaan kaikesta laskettavasta. Fysiologiaan liittyvät arvot muuttuvat, mutta silloinkin arvojen suhteellisuus säilyy.
Laskettavat esimerkit ovat aluksi tilastoituja ja tunnettuja arvoja. Laskettava voi olla mitä tahansa ja verrattavuus asioiden kesken on yllättävän samankaltaista. Tai, onko tämä yllätys? Laskettavat ovat konkreettisia tai abstrakteja esimerkkejä. Tämä on mielikuvaa, jota vastaavat käsitteet valo ja varjo. Todellisuudessa emme voi koskettaa kumpaakaan. Silti valo paljastaa varjoissa yksityiskohtia. Laskenta paljastaa matemaattiset varjot tuotteissa ja ilmiöissä. (242)
69. Mitat - suhde 1,618

100 mm = 10 cm
61,8 mm = 62 mm = 6,2 cm
100 mm /1,618 = 61,8 mm = 6,2 cm
Mitta 38,2 mm = 38 mm = 3,8 cm
100 mm - 61,8 mm = 38,2 mm = 3,8 cm
Mittanauhan pituudet 6,2 cm ja 3,8 cm sisältyvät kultaisen leikkauksen suhteeseen 1,618. Suhteellisuus ei ole desimaaleja, vaan ymmärrystä ilmiöiden keskinäisen aseman muodostumisesta. Kuvan mitat ovat siten keskinäisessä asemassa toisiinsa nähden, kuten asiat ovat keskinäisessä suhteessa toisiinsa nähden. Yhden arvon tietämällä muut tunnetaan. Mittojen keskinäiset asemat ovat todellisuudessa esiintyvä suhteellisuus asioissa ja arvoissa, eivät vain valokuvaan asetettuina mittoina.
Tuntemalla kultaisen leikkauksen suhdeluvun 1,618, sekä suhteellisuuden asioissa ja arvoissa, tiedetään mitan 3,8 cm vertaistiedoksi 6,2 cm ja nämä yhdistämällä tunnetaan kokonaisuus 10 cm.
Tunnettu arvo 3,8 cm => toinen arvo on 3,8 cm x 1,618 = 6,18 cm = pyöristettynä 6,2 cm
Kokonaisuus on 3,8 cm + 6,2 cm = 10 cm. (631)
21.6.2018*08:00
www.karikolehmainen.com
epcalculation@gmail.com
|