Fysiikan toiset perusteet
1. Aika.
2. Platonin luolavertaus.
3. Oleta pyöreä lehmä (The Fear of Physics)
4. Metafysiikka.
5. Demokritos 460 - 370 eKr.
6. Kultainen sääntö
7. Kultainen leikkaus
8. Ikkunalasin valuminen.
9. Domino vaikutus.
10. Kemiallisten aineiden jaksollinen järjestelmä.
11. Metallikappaleen hidas palaminen.
12. Arvojen syntyminen
13. Suhteellisuusteoria.
14. Viisi vaikuttavaa voimaa
14.1 Heikko ydinvoima
14.2 Vahva ydinvoima
15. Aikadilaatio.
16. Ajan käyristyminen.
17. Ketjureaktio.
18. Maapallon suhteellisuus.
- Aikadilaatio
18.1 Maapallon säde
18.2 Kultainen leikkaus
18.3 Viisi porrastusta
19. Foucaultin heiluri
- Aikadilaatio
20. Luonnollinen kävelyvauhti
21. Jarrutusmatka fysiikassa
.......................
30. Auton pysähtymismatka
31. Auton pysähtymismatka logaritmisesti
32. Teräksen yksikköympyrä ja alumiini
33. Johannes Keplerin ellipsikuvaus planeettojen kiertoradoista
34. Näkemisen geometria fysiikkana
- Aikadilaatio
35. Teräsköyden tuotesarjan muodostuminen
- Aikadilaatio
36. Vivun käsite
37. Valonnopeus painovoimaksi
38. Painovoima
38.1 Gravitaatiovakio
38.2 Painovoima maan päällä
38.3 Painovoima kuussa
39. Kappaleen vapaa putoaminen
40. Taipuminen yleisesti
...........................
51. Ulotteisuudet
51.0 Nollaulotteisuus - piste
51.1 Yksiulotteisuus - viiva - pituus
51.2 Kaksiulotteisuus - (poikkileikkauksen) pinta-ala - lujuus - 1,25
51.3 Kolmeulotteisuus - tilavuus - avaruus - 1,618
52. Aika neljäs ulotteisuus
53. Kaksosparadoksi
54. Energialla on massa
54.1 Nopeus ja massan kasvu
55. Aikamatkailu suhteellisuuden rajoissa
1. Aika
Seuraava on kuvaus ajan syntymisestä, johon maapallo ja sen asukkaat, eivät vielä kuulu, niiden syntyessä myöhemmin. Valokuvan energiakuplakin on mielikuva, kenties suklaan sulamisesta. Sen sijaan suhdelaskennan kuvaus ja selitys materialle, on laskimella tarkistettava todellisuus. Kokonaisuuden muodostuessa asioiden ja arvojen nivoutuessa toisiinsa ja muodostaessa suhdelaskennan.
 Alkuräjähdys tapahtui ajan alussa 13,7 miljardia vuotta sitten. Ymmärryksemme mukaan - ei missään - energiaa purkautui ja laajeni sekunnin murto-osassa äärettömyyteen. Alkuräjähdys tapahtui ajan alussa 13,7 miljardia vuotta sitten. Ymmärryksemme mukaan - ei missään - energiaa purkautui ja laajeni sekunnin murto-osassa äärettömyyteen.
Maailmankaikkeus laajeni kaikkiin suuntiin, aika käynnistyi ja syntyi suhteellisuus ilmiöihin. Tästä syystä voimme laskea asioita suhteellisina.
Englannin kielinen nimitys Big Bang oli alun perin pilkkanimi.
Ajan suhteellisuuden on opittu viimeiseksi. Välittömästi ajan syntymisen jälkeen, ei ollut suhteellisuutta, sen vuoron tultua myöhemmin. Maailma laajeni äärettömyyteen, siksi tarvitsemme äärettömän tapahtuman toiseksi ääripääksi, toisen ääripään muodostaessa yksittäisen tapahtuman. Välittömästi alkuräjähdyksen jälkeen ei syntynyt materiaa, massaa, atomeja tai aineen rakennetta. Kaikki oli energiaa tilanteena, johon nykytiede pyrkii hiukkaskiihdyttimillä. Kokeissa on päästy tilanteeseen, vastaten noin sekuntia räjähdyksestä. Tällöin energia oli jo muuttanut muotoa ja materiaa tiivistynyt.
E = m c 2
Albert Einsteinin suhteellisuusteoria aiheutti aluksi hämmennystä ja vastusta. Kaavan vasen puoli energia = merkin jälkeen tiivistynyt materiaksi. Kaavaan sisältyy suhteellisuus, johon laskenta perustuu. Maapallo saa energiaa auringosta, josta saadun liikkeen gravitaatiovoimat kumoavat. Tarkennettuna gravitaatiovoimasta vähennetyllä keskipakoisvoimalla eli jäljelle jäävällä painovoimalla. Voi ajatella vaikka veden kiertoa pilviin ja sen satamista vuorille. Veden valuessa vuoren rinnettä alas, saadaan tästä liikemääräenergiasta sähkövirtaa vesivoimalaitoksissa. Junat käyttävät virtaa liikkeeseen, hukaten energian painovoiman aiheuttamana kitkana. (1045)
2. Platonin luolavertaus
Platon käytti luolavertausta, jossa hän vertasi ihmisen asemaa luonnon kaavion luolassa asuvaan ihmiseen. Vertauksen todellisuuden kuva syntyi esineiden muodostamina varjoina luolan seinälle. Tämä tapahtuu siten, että todelliset esineet auringon valossa, vaihtoehtoisesti nuotion valossa heittävät varjon luolan takaseinälle. Luola-asukkaiden tavoin nykyihminen raapii todellisuuden pintaa aistiensa ja kykyjensä rajoissa. Luolaan tuotiin vankeja, joista osa oli nähnyt vain seinälle hahmottuvat varjot.
Platon
Vangit hahmottavat varjon perusteella tynnyrin suorakaiteeksi. Tynnyrin tyhjennettyä, sen tuo takaisin toinen miehistä, kantaen tynnyriä molemmista reunoista kannattaen eli vaaka-asennossa. Valon sijainti on nyt tynnyrin pituusakselin suuntainen miehen kulkiessa ohitse. Seinälle muodostuu tästä pyöreä kuvio. Kolmantena tapauksena tynnyri kulkee ohitse vinossa asennossa, jolloin näkee ovaalin muotoisen varjon heijastuvan luolan seinälle. Näiden havaintojen perusteella, ohitse kulki kolme erilaista "esinettä", vaikka kyse on samasta tynnyristä.
Platonin luolavertauksessa vanki vapautetaan. Vanki vastustaa siirtoa pois luolasta, mm. kirkkaan päivänvalon vuoksi. Totuttuaan valoon ja nähtyään todelliset esineet ja maailman, vanki joutuu palaamaan takaisin tyrmään. Muut vangit eivät nyt usko hänen kertomaa todellisesta maailmasta. Mikäli palautettu vanki yrittäisi vapauttaa muut vangit, nämä todennäköisesti tappaisivat hänet. Vertauksessa on paljon muutakin, joskin edellä oleva on kuvaus pääpirteissään. (74)
Platonilla oli ajatus valosta kaiken takana. Muutamia vuosia myöhemmin Albert Einstein teki saman havainnon valon nopeutena.
Suhdelaskennan ilmiöt ovat kuin tynnyreitä. Ne näyttävät erilaisilta, mutta ovat lopulta samaa tarkoittavia keskenään.
3. Oleta Pyöreä lehmä (The Fear of Physics)
Kirjan tekijä, amerikkalainen teoreettinen fyysikko Lawrence Krauss, Art House kertoo fyysikon kauneudentajun ratkaisevasti vaikuttaneen vuosisatamme maailmankuvan muodostumiseen.
"Seinällä olevista irrallisista heijastuksista onnistuttiin jotenkin arvaamaan suorien aistimustemme taustalla oleva yhtenäisyys". Edellä oleva liittyy Platonin kuvaukseen varjoista luolan seinällä ja tietämykseen, jonka fysiikka vaikkapa hiukkasfysiikan yhteydessä tänä päivänä tutkijalle paljastaa. Tämän perusteella Platonilla oli mielessä heijastuma sähkö-magnetismin ja heikon vuorovaikutuksen olemuksesta, jotka ovat yhden fysikaalisen perusteorian erilaisia ilmentymiä.
Edellä oleva kirjoitettuna meidän ajassa. Tieteen todetessa, Platonin olleen ajatuksineen vuosituhansia ajastaan edellä.
Platon käsittelee kirjoituksissa metafysiikkaa, jälkifysiikkaa. Mitä metafysiikka merkitsee, on määritelmänä tarkentamaton ja toisaalta todistamatonta. (537)
4. Metafysiikka
Platon 427 - 347 eea.
Hän oli Sokrateen kuuluisin oppilas ja Aristoteleen opettaja. Platon kirjoitti metafysiikasta, yhtenä yleisenä tulkintana siitä on; perinteisesti on ajateltu metafysiikan yrittävän tavoittaa ihmisen tiedon, havaintojen ja harhojen taakse ja kertovan totuuden perimmäisistä asioista. Jotta metafysiikka olisi mahdollista, tämän pitäisi olla luonteeltaan lopullinen todellisuus - ainakin periaatteessa - ja olla ihmisen ymmärrettävissä. Todellisuuden olisi rakennuttava siten, että se olisi inhimillisesti ymmärrettävää ja loogisesti ajateltavaa. Tässä on aluksi metafysiikasta, perustuen todistamattomaan oletukseen.
Platon erotti varman ja epävarman näkemyksestä. Tarkastelut olivat johdettuja erilaisista ilmiöistä maailmassa, jolloin tiedolla oli yhteys ikuisiin muotoihin ja idoihin. Mielenkiintoisesti samaa tarkoittavalla suhdelaskennalla on vastaavan kaltainen tapa kuvata ilmiöitä, kuten esimerkiksi viidellä Platonin kappaleella. Näkemisen geometria käyttää laskemiseen muotoja ja niiden ominaisuuksia liittyneeä todellisuuteen. Tätä esitetään esimerkiksi lujuuden laskennan yhteydessä.
Metafysiikka
Näkemisen geometrian esimerkki
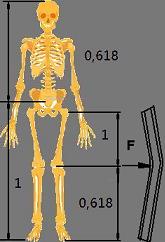
Luuranko ihmisessä kannattaa elimistöä. Koneenrarkennuksen asennuksessa runko on osa, joka kannattaa sen rakennetta.
Molemmilla on sama toiminto ja tarkoitus, jonka kuva osoittaa. Terästangolla kuvassa kuormaan nähden, on sama taipumasuhde kuin ihmisen elimistöllä väsymiseen. Tämä, kun pistemäinen kuormitus kannattajalla on kannattajan painon suuruinen. Tämä on ajatus, jossa ihminen kannattaa oman painonsa.
Lujuus ja taipuma sisältyvät molemmat kultaiseen leikkaukseen.
1 / 1,618 = 0,618
Naisen luuranko
Ihmisen luuranko ei ole terästä, mutta sen ominaisuudet noudattavat sitä.
5. Demokritos 460 - 370 eKr.
 Hän kirjoitti Babyloniassa ja Meroessa; vieraili Egyptissä ja Diodorus Siculus toteaa hänen asuneen siellä viisi vuotta. Hän julisti, ettei yksikään hänen aikalaisensa ollut tehnyt enemmän matkoja, nähnyt enemmän maita, ja tavannut enemmän tutkijoita kuin hän. Erityisesti hän mainitsee Egyptin matemaatikot, joiden tietoja hän kehui. Myös Theophrastus puhui hänestä miehenä, joka oli nähnyt monia maita. Matkoillaan Diogenes Laertioksen mukaan, hän tutustui kaldealaisiin tietäjiin. Hän kirjoitti Babyloniassa ja Meroessa; vieraili Egyptissä ja Diodorus Siculus toteaa hänen asuneen siellä viisi vuotta. Hän julisti, ettei yksikään hänen aikalaisensa ollut tehnyt enemmän matkoja, nähnyt enemmän maita, ja tavannut enemmän tutkijoita kuin hän. Erityisesti hän mainitsee Egyptin matemaatikot, joiden tietoja hän kehui. Myös Theophrastus puhui hänestä miehenä, joka oli nähnyt monia maita. Matkoillaan Diogenes Laertioksen mukaan, hän tutustui kaldealaisiin tietäjiin.
Demokritos oli ensimmäinen, joka ymmärsi, että Linnunrata, koostuu todellisuudessa kaukaisten tähtien valosta.

Demokritos
Teoria atomeista näyttää olevan enemmän linjassa modernin tieteen kanssa, kuin mikään muu teoria antiikin ajalta. Kuitenkin samankaltaisuus modernin tieteen käsitteen kanssa voi olla hämmentävää, kun yrittää ymmärtää mistä hypoteesi tuli.
Democrituksen (ja Leukippos) teoria totesi, että kaikki koostuu "atomeista", jotka ovat fyysisesti, mutta ei geometrisesti jakamattomia, atomien sisällä sijaitsee tyhjää tilaa. Atomit ovat häviämättömiä, näin on aina ollut, ja näin tulee aina olemaan. Ne ovat aina liikkeessä, että on olemassa ääretön määrä erilaisia atomeja, jotka eroavat toisistaan muodon ja koon puolesta.
Tämä perustana fyysiseen maailmaan, Democritus pystyi selittämään kaikki maailman muutokset atomien liikkeiden muutoksena tai muutoksina, miten ne olivat pakattu yhteen. Tämä oli merkittävä teoria, joka yritti selittää koko fysiikan perustuen muutamiin ajatuksiin ja toi myös matematiikan osaksi fysikkaa, sillä koko rakenne Democrituksen ehdottamana oli määrällistä matemaattisia lakeja noudattavaa. Toinen keskeinen ajatus Democrituksen teoriassa on, että luonto käyttäytyy kuin kone, se ei ole mitään muuta kuin erittäin monimutkainen mekanismi.
Bertrand Russell totesi, että he vain osui onnekkaasti hypoteesiin, josta vasta äskettäin on vahvistettu näyttö.
(639)
6. Kultainen sääntö
Arkhimedes
Kaksi kappaletta on tasapainossa, kun niiden etäisyys on tukipisteestä on käänteisessä suhteessa niiden massaan. Kiinteän tukipisteen avulla voisi vivuta maapallon paikoiltaan. Tästä on kulunut jokseenkin kauan, huomaamatta arvon löytyvän vastaavalla periaattella.

Wikipedia
Jokainen punnitseva kauppias tiesi vaa'alla mittaamisen perusasian:
Varsiltaan ja painoiltaan yhtä pitkä vaaka, ei taivu vasemmalta tai oikealta puolelta.
Kultainen sääntö oli helppo johtaa tästä, mutta kuka sen tekee on historia osoittanut vaikeaksi. Luonto pyrkii symmetriaan, joka saavutetaan voiman ja etäisyyden tulona.

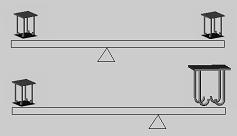
”Mikä matkassa hävitään, se voimassa voitetaan”.
Kultainen sääntö tasapainoehdolle vastaa arvojen välistä suhdetta. Arvojen välinen etäisyys, vastaa vipuvarren käsitettä. Tunnetun varren pituudella, tuntemattoman arvon voi määrittää. Punnitseminen materiassa merkitsee lineaarista tarkastelua, mutta arvojen yhteydessä käyrällä, jonka tarkastelu hallitaan suhdelaskentana. Vipuvarrella tasapainotetaan tuntematon arvo tunnettuun arvoon laskemalla. Arvot voivat olla konkreettisia tai arvomaailmaan liittyviä, kuten jarrutusmatka, tuotteen paino jne.

Muurahainen 1
1 1
1 2 1
1 3 3 1
Elefantti 1 4 6 4 1
Pascalin kolmion riviarvo väsyy matkalla, kuten juoksija matkalla tai tuotesarja. Kun tuote on pieni muurahainen, se saa arvon 1. Muurahainen kantaa kymmeniä kertoja oman painonsa verran, mutta norsu ei kanna edes oman painonsa suuruista kuormaa. Pascalin kolmio on samaa tarkoittavaa ilmiöiden kanssa. Juoksijoiden ajat ovat kaikkien ymmärtämä todellisuus. Siirryttäessä materiaan ja tuotteen arvon muodostumiseen, usea lukijoista ei ymmärrä kirjoitettua. Siksi aloitamme sellaisesta, joka on tilastona tarkasteltavaa. Fysiologia ei poikkea materiasta tai tuotteiden arvon muodostumisesta, muuten kuin tarkastelutavan puolesta.
Planeetat suurimpina tuotteina
Laskenta voi asettaa vaakaan käsitteellisen asian punnittavaksi ja yhdistämällä Arkimedeksen nosteen käsitteen, voi punnita ominaisuuksia aineettomasta. Arkimedes ei kyennyt määrittämän onton ominaispainoa, jolloin laskenta määrittää myös "onton" ominaisuudet. meillä on abtrakti punnitsemisen käsite, josta esimerkkinä vaikka käyrän arvojen määrittäminen käyrälle, jota ei ole määritetty. (278)
7. Kultainen leikkaus
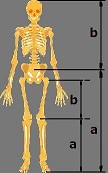 Jakamaton kokonaisuus suhteutuu suurempaan osaan samassa suhteessa, kuin tämä suhteutuu pienempään jaettuun osaan. Kultainen leikkaus on irrationaalinen vakio 1.61803398874989. Filosofiassa rationaalinen merkitsee järjen käyttöä päätöksentekoon ja irrationalisuus vastakohtaa. Jakamaton kokonaisuus suhteutuu suurempaan osaan samassa suhteessa, kuin tämä suhteutuu pienempään jaettuun osaan. Kultainen leikkaus on irrationaalinen vakio 1.61803398874989. Filosofiassa rationaalinen merkitsee järjen käyttöä päätöksentekoon ja irrationalisuus vastakohtaa.
Muita nimityksiä suhteelle ovat kultainen jako ja suhde. Laskennassa kultaisesta leikkauksesta käytetään kreikkalaista pientä kirjainta fii φ.

Golden ratio
a) Kantapäästä polveen - Kantapäästä napaan -
b) Polvesta lonkkaniveleen - Navasta pään päälle
( a + b ) / a = a / b = (fii) = 1,618 033 988
5 / 3 /1,03 = 1,618 5 > Laskennan suhteellisuusraja < 5 8 / 5 = 1,6
Kaikilla elävillä ja koneiden elimillä on tämä suhde.
Toisin sanoen
Katkaise tanko 100 cm kahteen osaan siten, että pitempi osa on 61,8 cm. Tanko on leikattu kultaisen leikkauksen suhteessa 100 cm /61,8 cm = 1,618.
Lyhyemmän osan pituus on 38.2 cm. Kultainen leikkaus antaa nimityksenä väärän mielikuvan, kuin leikkaaminen tietyssä suhteessa. Kultainen leikkaus on materiaan liittyvä kerroin, määrittäen voimien keskinäistä suhdetta. Vaarallinen leikkaus on käsite, jonka mallintamiseen voi käyttää alla olevaa piirrosta.
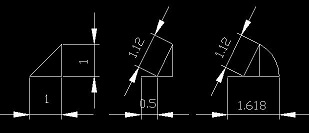
Kultainen leikkaus näkemisen geometriana
Pascalin kolmion rivien välinen kerroin 1,1, sekä lujuuslaskennan kerroin 1,12. "Katkaiseminen" voi jatkua viisi kertaa, jonka jälkeen suhteellisuusraja ylittyy. Saman voi kokeilla taittamalla paperin siististi viisi kertaa. (21)
8. Ikkunalasin valuminen
 Vanhoissa rakennuksissa on ikkuna-laseja, jotka ovat alalaidasta paksumpia kuin yläreunasta. Meille opetettiin lasin olevan nestettä, joka vuosien saatossa valui alaspäin ja näin syntyi lasin alareunan paksuneminen. Nykytietämyksen mukaan lasin valumista ei tapahdu tarkastelujaksossa, jonka lasit ovat ikkunoissa. Tiede sanoo; tasolasina valmistetun lasin olleen epätasaisen paksuudeltaan, jonka seurauksena leikatun ikkunalasin paksu reuna sijoitettiin alareunaan tasapainoiseksi vaikutelmaksi. Vanhoissa rakennuksissa on ikkuna-laseja, jotka ovat alalaidasta paksumpia kuin yläreunasta. Meille opetettiin lasin olevan nestettä, joka vuosien saatossa valui alaspäin ja näin syntyi lasin alareunan paksuneminen. Nykytietämyksen mukaan lasin valumista ei tapahdu tarkastelujaksossa, jonka lasit ovat ikkunoissa. Tiede sanoo; tasolasina valmistetun lasin olleen epätasaisen paksuudeltaan, jonka seurauksena leikatun ikkunalasin paksu reuna sijoitettiin alareunaan tasapainoiseksi vaikutelmaksi.
Vanhoissa rakennuksissa on tosiasia paksumman reunan sijaitsevan lasin alareunassa ja on luontevaa sijoittaa paksumpi lasin kohta ruudun alareunaan. Lasimateriaali on ollut arvokasta, jolloin köyhän "töllin" ikkunoiden voi olettaa olevan lasin epätasaisinta aluetta. Tästä johtuen lasin paksumpi osuus voi sijoittua keskelle ikkunaa. Oletteko nähnyt kuvaamaani ikkunalasia? Tutkin kesällä 2007 vanhoja kirkkoja, joiden ikkunoista todellakin löysin paksumman kohdan muualtakin, kuin lasin alareunasta. Lähes kaksituhatta vuotta myöhemmin, ei vielä ollut varmuutta, valuiko lasi ikkunoissa vai ei. Roomalaiset alkoivat käyttää lasia ikkunoissa 300-luvulla. Tästä johtuen metafysiikan havainnon tekemiseen voi olettaa menevän enemmän aikaa.
Oliko ikkunalasin valuminen vaikeaa havaita, jos lasi ei valu? Olimmeko kenties näennäistieteen alueella, vai kuinka asian muotoilisimme? Pitääkö asioiden olla niin ehdottoman oikeita ja vääriä ja mitä haittaa ikkunalasin valumisesta tai valumattomuudesta aiheutuu? Kenties metafysiikan (jälkifysiikan) vuoro on seuraavana? (281)
9. Domino vaikutus
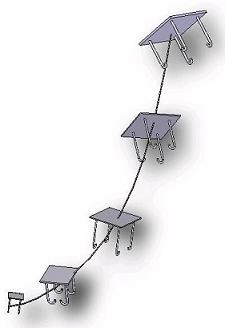
Ketjureaktio ilmenee, kun pieni muutos aiheuttaa vastaavan kaltaisen muutoksen läheisyydessä. Tämä tapahtuu lineaarisessa järjestyksessä kuten viivan pisteet. Varjot alla olevassa kuvassa esittävät saman kuin palikat. Mikäli ensimmäinen dominopalikka kaatuu, tiedämme viimeisen palikankin kaatuvan kuvan tapauksessa. Laskettaessa tiedämme arvon jostakin, jolloin tiedämme arvon toisista, jotka ovat samalla käyrällä. Edellä oleva tarkoittaa vastaavien tapauksien löytyvän yhteiseltä käyrältä. Ilmiöt ja tuotteet kuuluvat niiden omille käyrille. Edes asioiden oleminen samalla käyrällä, ei ole välttämätöntä, mutta siitä myöhemmin. Valokuvassa dominopalikat muodostavat esimerkin käyrästä.

Kerrottu Platonin luolavertaus muodostui konkreettisista todellisuuden varjoista, mutta varjoja on monessa muodossa. Kuormapalkin ollessa kuormitettu, sen varjo on mitattavaa taipumaa. Varjo eli taipuma kertoo tarvittavan palkista. Kilpajuoksun yhteydessä, varjo on aikaa, jolloin käytetty aika kertoo tarvittavan tapahtumasta.
Laskenta on enemmän kiinnostunut fysiikasta ja tuotteiden muodostumisesta, joskaan mikään inhimillinen ei jää ulkopuolelle. Seuraava on esimerkki käyrästä, jollaisen tuotteet ja ilmiöt esittävät niiden arvoina. (810)

10. Kemiallisten aineiden jaksollinen järjestelmä
 Alkuaikoina kemistit huomasivat, että aineita ei voi sotkea keskenään miten sattuu. Tietyt suhteet säilyivät aineita sekoitettaessa. Tämä oli todiste atomien puolesta. Atomipainoihin ei aluksi kiinnitetty huomiota, sillä näiden mittaaminen oli hankalaa. Atomipainoissa ei ensin ollut havaittavaa yhteneväisyyttä, kun havaintoja oli vasta kuudestakymmenestä alkuaineesta. Näytti, ettei atomipainolla ollut tekemistä aineen kemiallisen ominaisuuden kanssa. Venäläinen Dimitri Mendelejev (1834-1907) valmistui kemistiksi ja alkoi valtion palkkalistoilla luokitella öljyjä. Tässä työssä hänelle tuli mieleen luokitella aineet, alkuaineet mukaan lukien. Alkuaikoina kemistit huomasivat, että aineita ei voi sotkea keskenään miten sattuu. Tietyt suhteet säilyivät aineita sekoitettaessa. Tämä oli todiste atomien puolesta. Atomipainoihin ei aluksi kiinnitetty huomiota, sillä näiden mittaaminen oli hankalaa. Atomipainoissa ei ensin ollut havaittavaa yhteneväisyyttä, kun havaintoja oli vasta kuudestakymmenestä alkuaineesta. Näytti, ettei atomipainolla ollut tekemistä aineen kemiallisen ominaisuuden kanssa. Venäläinen Dimitri Mendelejev (1834-1907) valmistui kemistiksi ja alkoi valtion palkkalistoilla luokitella öljyjä. Tässä työssä hänelle tuli mieleen luokitella aineet, alkuaineet mukaan lukien.
Hän sijoitti aineet atomipainojen mukaan ja oletti osan alkuaineista olevan löytämättä ja osan punnituista atomipainoista vääriksi. Näin hän sai alkuaineet sijoittumaan säännön mukaisiin paikkoihin. Tunnemme tämän alkuaineiden jaksollisena järjestelmänä. Samaa tarkoittava suhdelaskenta on paljossa samaa alkuaineiden jaksollisen järjestelmän kanssa. (92)
11. Metallikappaleen hidas palaminen
 Ranskalainen kemisti Antoine Laurent de Lavoisier (26.08 1743 - 08.08 1794), julkaisi aineen häviämättömyyden lain. Tieto on tärkeä kaavan E = m c2 kannalta. Tunnisti ja nimesi hapen 1778, osoittaen kokeellisesti palamisen olevan prosessin, missä palava aine ja happi yhtyvät. Ranskalainen kemisti Antoine Laurent de Lavoisier (26.08 1743 - 08.08 1794), julkaisi aineen häviämättömyyden lain. Tieto on tärkeä kaavan E = m c2 kannalta. Tunnisti ja nimesi hapen 1778, osoittaen kokeellisesti palamisen olevan prosessin, missä palava aine ja happi yhtyvät.
Hän osoitti ensimmäisenä päällepäin erilaisen olevan osa samaa kokonaisuutta. Kivet, puut ja kaikki maailman massa olivat samaa kokonaisuutta. Tämä tietoisesti, pyrkien selittämään kokeet yhdellä teorialla.
Ruostuminen

De Lavoisier kiinnostui seuraamaan mm. pitkäkestoista metallikappaleen ruostumista. Häntä kiinnosti tietää painoiko kappale ruostuttuaan enemmän vai vähemmän.
De Lavoisier was interested to study the long-lasting corrosion of metal piece. He was interested to know the weight after corrosion, was that more or less.
Vaihtoehtoja
a) kappale painaa vähemmän
b) kappale painaa enemmän
c) kappaleen paino ei muutu
Valokuvasta näkee, kuinka lokasuoja on syöpynyt. Samalla materiaali on menettänyt lujuuden. Nämä eivät ole syöpyneet suljetussa systeemissä painon toteamiseksi. Antoine Laurent de Lavoisier ei tyytynyt arvaamaan painon muutosta. Hän pystytti olohuoneeseen täysin suljetun laitteiston. Kokeita nopeuttaakseen he - vaimonsa kanssa - lisäsivät erilaisia aineita, lämmittivät ja lopulta polttivat materiaa nopeuttaakseen tapahtumaa. Jokaisen kokeen jälkeen havaiten saman. Kappale painoi enemmän. Lisääntyneen määrän painoa he pystyivät määrittämään poistuneesta ilmamäärästä. (923)
12. Arvojen muodostuminen
12.1 Konkreettiset arvot
Arvot syntyivät alkuräjähdyksen yhteydessä. Mitattavia, käsin kosketeltavia arvoja ovat kappaleen pituus, leveys ja korkeus. Nämä ymmärretään parhaiten kappaleeseen liittyvinä mittoina.
Ominaisuuden käsin kosketeltavalle antaa siihen sisältyvä arvo. Arvoa voi kutsua varjoksi, sillä sekin muodostuu konkreettisesti olevasta. Kivellä ja kävyllä voi heittää kohdetta. Kävyn keveys ja pehmeys tekevät siitä todennäköisemmän valinnan, halutessa olla satuttamatta tai rikkomatta. Suhdelaskenta mahdollistaa käsitteellisen, käsin koskemattoman arvon tarkastelun. Tietokoneella luodaan kolmeulotteisia näköismalleja, jotka ovat katsottavia, mutta ei kosketeltavia. Mallista ei tästä johtuen tiedä, miltä ne tuntuvat. Arvot ovat yksiulotteisia, tarkoittaen arvolla saatavaa tietoa kohteesta, kuten pituus, paino, kovuus, lämpö, taipuma jne. Alla olevaan viisikulmioon, käsin kosketeltavat arvot muodostavat alaosan kolme särmää.
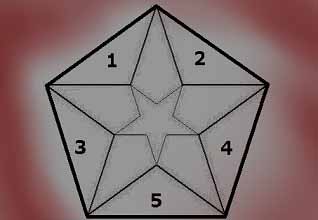
1. Suhteellisuus
2. Aika
3. Pituus
4. Korkeus
5. Leveys
12.2 Abstraktiset arvot
Alkuräjähdyksen yhteydessä syntyi arvoja, joita ei näe, kuten aika. Ajan käsite on suhteellista, kuten se yleisesti mielletään. Toisissa asioissa tietty ajanjakso on pitkä, toisissa lyhyt. Näin myös eri henkilöiden tarkastellessa asioita, ne nähdään eri mittakaavassa ajan suhteen. Suhteellisuus on toisinaan suoraan verrattavaa, toisissa tapauksissa käsitteellisesti ymmärrettävää.
Esimerkkinä voimme valita halutut mittasuhteet. Valittuamme muodon, voi todeta vaikkapa tangon painavan 1 kg/m. Sahattaessa 2 m pitkä kappale tangosta, on valittu pituus, mutta ei siihen sisältyvää painoa. Painoksi tangolle tulee aina 2 kg saman mittaisessa kappaleessa. Saman kaltainen tilanne syntyy lukemattomissa asioissa, sillä tiedostamatta arvon määrittämällä, muutkin arvot määrittyvät.
Katkaise 0,1 m pituinen tanko ja aseta se tukien väliin, todeten tanko jäykäksi. Sahaa toinen tanko kaksi kertaa pitempänä, jolloin se vastaavasti tukien päällä taipuu noin kaksi kertaa enemmän. Voitteko sanoa, paljonko tanko taipuu 42 m pitkänä? Toteatte, ettei sellaista tangon pituutta ole. Sanotte tangon taipuvan kahdeksankertaisesti, kun jänneväli kasvaa kaksinkertaiseksi. Jännevälin vaikutus taipumaan, on kaavassa kolmanteen potenssiin. Tässä olette väärässä, sillä tarvitsee vain muuttaa ajatusten kulkua. 100 m pikajuoksija on jäykkä kuten esimerkin tanko, väsymättä eli taipumatta sadan metrin matkalla. Juoksija ei väsy myöskään 200 m matkalla, jolloin suoritukseen kuluva aika on kaksi kertaa sadan metrin juoksuun käytetty aika. Juoksija kykenee myös maratonin matkaan, taipuen ajan lisääntymisenä. Molemmat juoksut ovat laskettavaa arvoina.
Viisikulmio kuvaa suhteellisuutta. Esitetyssä viisikulmiossa on kolme määritettävää ulotteisuutta eli pituus, leveys ja korkeus. Muuttuva aika (dilaatio) liikkuvaan ja paikalla pysyvään, sekä kiinteä suhteellisuus. Näiden kautta menettely on laskettava todellisuus. Jotkut asiat ovat etenemää, toiset pinta-alaa ja eräät tilavuuteen perustuvaa laskentaa. Tehtävän voi usein laskea ristiin monessa merkityksessä.
Entä aika? Kaikella on vastapari kuten kylmä - kuuma, valkoinen - musta jne. Aika liitetään ilmiön kuvaamiseen ja mielletään liikkeeseen. Samaa tarkoittavassa suhdelaskennassa ei niinkään sekunteina, vaan aikadilaationa. Näin aikaa tarkastellen, se liittyy aika-avaruuteen, yhtä hyvin kuin arvoavaruuteen tuotteissa ja ilmiöissä. (258)
13. Suhteellisuusteoria

1. Suhteellisuusteoria
1.1 Suhteellisuusteoria perustuu Albert Einsteinin kahteen teoriaan, erityiseen (1905) ja yleiseen suhteellisuusteoriaan (1916). Erityinen suhteellisuusteoria on nykyinen fysiikan käsitys tilasta, ajasta ja sähkömagnetismista. Yleinen suhteellisuusteoria puolestaan on erityisen suhteellisuusteorian laajennus, joka selittää painovoiman.
1.2 Avaruus : tilaa ja aikaa on tarkasteltava yhdessä ja suhteessa toisiinsa .
1.3 Valonnopeus on muuttumaton ja sama kaikille sitä tarkasteleville
1.4 Mittauksien kestot ovat suhteessa tarkkailijoiden nopeuksiin. Erityisesti avaruuden pituuden supistumiseen ja aikadilaatioon.
2. Yleistä suhteellisuusteoriasta
Yleisen suhteellisuusteorian perustava idea on avaruuden rakenne. Fysiikan yhteisö hyväksyi erityisen suhteellisuusteorian vuonna 1920. Teoriasta tuli nopeasti merkittävä ja tarpeellinen väline teoreetikoille ja kokeiden tekijöille uusilla aloille atomifysiikkaan, ydinfysiikkaan ja kvanttimekaniikkaan. Toisaalta, yleinen suhteellisuusteoria ei näyttänyt olevan niin hyödyllinen. Sille näytti olevan vähän käyttöä, useimpien sovelluksien ollessa tähtitieteellissä mittakaavoissa. Teorian käyttö tuntui tästä syystä rajoittuvan pieniin korjauksiin Newtonin gravitaatioteoriassa.
3. Teoria suhteellisuudesta
3.1 Sata vuotta erityisen suhteellisuusteorian jälkeen, teoria suhteellisuudesta täydentää yleistä suhteellisuusteoriaa ja selittää, kuinka tähtitieteellisissä mittakaavoissa tunnistetut asiat vaikuttavat maan päällä pienellä nopeudella. Tämä esitetään samaa tarkoittavana suhdelaskentana.
3.2 Eräs tieteen suurista virhepäätelmistä on ollut aikadilaation liittyminen ainoastaan suurella nopeudella tapahtuviin ilmiöihin. Kilpajuoksijat juoksuradalla ovat saman maailmankaikkeuden lainalaisuuden alaisia, kuin suurella nopeudella liikkuva raketti. Todellista lähes valonnopeuden saavuttavaa rakettia, ei kenties koskaan kyetä valmistamaan.

3.3 Ensimmäinen perustelu on Albert Einsteinin teoria, jota ei ole käytetty pienellä nopeudella tapahtuviin ilmiöihin, vaikka seuraava lause kehoittaa tähän.
Erityinen suhteellisuusteoria koskee kaikkia fysikaalisia ilmiöitä
14. Viisi vaikuttavaa voimaa
Ei ole kauan siitä, kun tunnettiin kolme vaikuttavaa voimaa;
- sähköinen voima - magneettinen voima - gravitaatio eli painovoima
Radioaktiivisuuden havaitsemisen jälkeen tapahtumien selittäminen ei ollut enää mahdollista kolmen voiman kautta. Tarvittiin lisää selittäjiä.

14.1 Heikko ydinvoima
Silloin arveltiin olevan jokin heikko voima. Perustelu heikkoudelle oli lähinnä se, että sitä oli vaikea mitata pienuuden ansiosta ja atomin mittaa kauempana olevat hiukkaset sen harvoin tunsivat.
14.2 Vahva ydinvoima
Vuonna 1911 atomilla selvitettiin olevan ydin. Edelleen havaittiin raskaimmilla atomeilla olevan ytimessä useampia protoneita ja näiden hylkivän toisiaan. Tämän vuoksi arveltiin olevan niitä koossa pitävä ydinvoima. Tätä kutsuttiin vahvaksi voimaksi. Newton oli ennustanut lyhyen kantaman voimien olemassaolon, kykenemättä heikkoa voimaa todentamaan.
Viisi voimaa kattaa luonnossa tavattavat ilmiöt. Muut voimat eivät vaikuta maailman toimintaan. Edellä oleva fysiikan tuntemana, jossa luku viisi liittyy suhdelaskentaan ilmiöiden selittämiseksi. Viisi materiassa vaikuttavaa voimaa tai kuormitusta saavat selityksen laskennan myötä. Lopulta kaikki on samaa, kuten alkuräjähdys kaikelle olevalle. Tulemme myöhemmin hahmottamaan asioita energian kautta. Laskenta perustuu lukuun viisi ja laskennan ulkoinen tunnus on viisikulmio. (195)
15. Aikadilaatio
Ajan vääristymä eli aikadilataatio on suhteellisuusteorian ennustama ominaisuus, jonka mukaan kappaleen liikkuessa lähellä valon nopeutta aika kulkee yhä hitaammin.
Oleellista on valon absoluuttinen nopeus, sillä liikumme millä nopeudella tahansa, valo liikkuu meihin nähden vakionopeudella. Tätä on kenties vaikeaa ymmärtää, mutta jollaiseksi todellisuus on osoittautunut. Taulukossa on massan kasvaminen nopeuden lisääntyessä ja aikadilaatio. Aikadilaatiossa suurella nopeudella; liikkeessä olevan aika hidastuu paikallaan olevaan aikaan nähden.
E = m c2
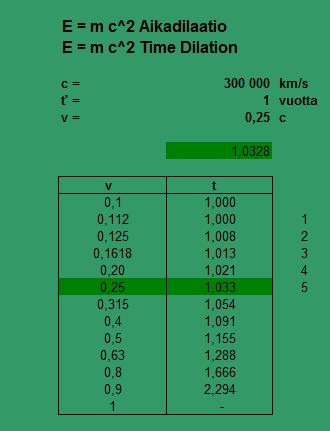
Valonnopeus päättyy taulukossa suhteelliseen arvoon 1. Valonnopeus on käsitteellinen arvo, jolloin arvon 1 jälkeen tapahtuvat jokapäiväisen elämän ilmiöt. Eräs suhdelaskennan tärkein kerroin on 1,25 (taulukossa arvo 0,25). Luku viisi ja viisi porrastusta ovat tärkeitä. Taulukossa arvo 0,25 ja viisi porrastusta liittyvät yhteen. Tärkeä on myös kerroin 1,03(28), liittyen kahteen edelliseen. Ilman kerrointa 1,03(28) on mahdoton laskea useita asioita. Osaamme laskea nopeutta ja aikaa, jolloin lisäämällä nopeutta 25 %, lyhenee aika 25 %. Ilmiöissä ja tapahtumissa näin ei tapahdu, vaan muutos on useassa tapauksessa aikadilaation määrittämä arvo (1,033).
Aikadilaatio ei ole itsestään selvyys. Aikadilaatio liittyy kultaiseen leikkaukseen, vaikka on tuntematonta suurelle osalle sivistynyttä maailmaa. Osa uskoo mieluummin ikiliikkujan mahdollisuuteen, mutta katsotaan, kuinka liike pysähtyy tällä tarkastelulla.
Sanotaan, että fyysikot piirtävät ensimmäiseksi ympyrän, kun aloittavat selittämään ilmiötä. En ole keksinyt tätä itse, vaan sen voitte lukea vaikkapa kirjasta Oleta pyöreä lehmä, jonka on kirjoittanut Nobel-palkitttu fyysikko Lawrence Krauss. Sallikaa minun aloittaa ympyrällä, joka on suuruudeltaan päiväntasaaja. (742)
16. Ajan käyristyminen
Tähdestä heijastuva valo taipuu ohittaessaan auringon. Valolla on nopeus, jolloin massaan sisältyy energia ja energialla on massa. Massat vetävät toisiaan puoleensa. Kaaviossa alla on vapaa kappaleen putoaminen maan pinnalla. Aika on on vaalea sininen käyrä kaaviossa 0,1 - 1 sekuntia. Ylempi käyrä on matka metreissä. Aika ei tietenkään oikeasti käyristy sekunnin aikavälillä, vaan tarkastelutavasta johtuen aika ja putoava kappale uurtavat käyrän arvoavaruudessa. Kuitenkin olemme lähellä sitä, mitä aika-avaruudessa tapahtuu,vaikkakin vain mielikuvana.
0,10 - 0,12 - 0,16 - 0,20 - 0,25 - 0,315 - 0,40 - 0,50 - 0,63 - 0,80 - 1,00
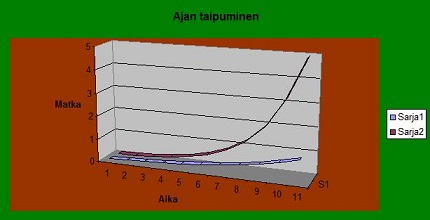
Aika Matka
t m
0,100 0,0491
0,125 0,0767
0,160 0,1256
0,200 0,1964
0,250 0,3068
0,314 0,4841
0,400 0,7856
0,500 1,2275
0,630 1,9487
0,800 3,1424
1,000 4,9100
m = 0,5 x g x t2
Avaruusmatkailussa lasketaan ajan vääristymistä (ja massan kasvua). Tätä kutsutaan aikadilaatioksi. Kaavio osoittaa kappaleen putoamisen aikana massan kasvavan nopeuden kasvaessa ja ajan taipuvan. Suuruus on tosin niin pieni, ettei sitä havaitse. Suhdelaskenta käyristää aikaa ilmiöissä, joita muuten ei kykene laskemaan. Tämä tulee esille fysiikkaan, fysiologiaan ja materiaan liittyvien ilmiöiden yhteydessä. Nämä ilmiöt eivät poikkea siitä, mitä avaruudellisessa maailmassa ilmenee. (527)
17. Ketjureaktio
Ketjureaktio ilmenee, pienen muutoksen aiheuttaessa vastaavan kaltaisen muuttuvan muutoksen läheisyydessä. Tämä tapahtuu logaritmisessa järjestyksessä käyräviivana.
Samaa tarkoittavalla suhdelaskennalla on mahdollisuus laskea tunnettua ja lisäksi aiemmin laskemattomia ilmiöitä, sarjaksi kuvattuna eksponentiaalisena käyränä. Suhdelaskenta perustuu valoon ja varjoon, pitkälti siten, kuten Platon näki sen omana aikanaan. Tämä perustuu Platoniin liitettyyn luolavertaukseen varjoista. On olemassa sanonta minkä taakseen jättää, sen edestään löytää ja näin on tässäkin tapauksessa.
Varjot pystyvät kuvaamaan asioita, jotka valossa jäävät näkymättömiksi. Vastaava tapahtuu valokuvaa kehitettäessä. Tummista osista kehitetyssä valokuvassa ei kenties erota kaikkia sen yksityiskohtia. Valottamalla seuraavaa valokuvaa enemmän, tulevat yksityiskohdat enemmän esiin. Valo ja varjo musta-valkonegatiivissa vaihtavat puolia, vaaleat osat negatiivista kehittyvät tummaksi osaksi valokuvaa ja päinvastoin.

Ilmiö kasvaa kuten tuotekäyrä kuvassa
Aikadilaatio on jossakin määrin vastaava tapahtuma, kuin valokuvan kehittäminen. Aikadilaatiokin määrittää vastakkaisuuksia, joista toinen liittyy ajan hidastumiseen ja toinen massan lisääntymiseen. Valokuvauksen ja ilmiöön liittyvän aikadilaation ero on ajassa. Jokainen valokuva saa oman yksilöllisen valotusajan parhaan tuloksen saavuttamiseksi, ilmiöissä paras tulos saa aina kiiinteän valonnopeuteen perustuvan aikadilaatiokertoimen 1,0328.
Aika hidastuu - massa kasvaa
Massaa voi koskea - aikaa ei voi

Valoa ja varjoa
Viivaa ja viivattomuutta
Järjellä tätä ei osaa selittää, mutta tehkää seuraava koe. Leikatkaa paperista ohut suikale ja piirtäkää paperin toiselle puolelle jatkuva viiva päästä päähän. Kiertäkää paperi kädessä 180 astetta ja liimatkaa päät yhteen. Paperi on kiertyneenä muodoltaan numero kahdeksan. mutta ennen kaikkea viivaa seuraamalla kierretään paperin kumpaakin puolta viivalla ja ilman viivaa. Olemme samaa tarkoittavan suhdelaskennan periaatteen ytimessä.
18. Maapallon suhteellisuus
Aikadilaatio
Maapallon ympärysmitta 40 (000 km)
Vuorokausi 24 tuntia
Suhteellinen maapallon pyörimisnopeus 40 /24 = 1,666...

Suhteellinen maapallon pyörimisnopeus, kultainen leikkaus
40 / (24 x 1,03) = 1,618
Proportional Earth's rotation speed, the Golden Ratio
18.1. Maapallon säde (aikadilaatio)
40 / (9,82 x 2 x 3,14.. x 1,0328) = 0,628 radiaania
40 maapallon ympärysmitta / (painovoima x D/2 = R x Pi x aikadilaatio = 0,2 Pi rad
18.2. Kultainen leikkaus (aikadilaatio)
40 / (2 Pi rad x 1,03) = 6,18
10 / 6,18 = 1,618
18.3. Viisi porrastusta
1,0 - 1,031 = 1,03 - 1,034 = 1,12 - 1,038 = 1,25 - 1,0316 = 1,6 - 1,0331 = 2,5
1. 2. 3. 4. 5.
Viisi porrastusta on suhteellisuuden raja, jonka havaitsee aikadilaatiosta. Ajattelette edellä olevan kuvauksen maapallosta. Maapallo on fysiikkaa muiden asioiden joukossa, kuten aikadilaatio ilmiöiden joukossa. (202)
19. Foucaultin heiluri (aikadilaatio)
Heilurin pyörähdysaika on laskettu väärällä perusteella. Aivan kuin heilurilla ei olisi merkitystä, tuli ajaksi mikä tahansa.


Heiluri on nimetty ranskalaisen Leon Foucaultin mukaan. Yksinkertainen heiluri, jossa pistemäinen massa on ripustettu massattomaan ja venymättömään vaijeriin. Ensimmäinen koe tehtiin vuonna 1851 Pariisissa, Pantheonin kupoliin. Kokeella osoitettiin maapallon pyörivän akselinsa ympäri, jonka koe erinomaisesti osoitti. Heiluri pyörähti tasossa ympäri myötäpäivään 11 astetta tunnissa eli kokonaisen kierroksen 32,7 tunnissa. 360 astetta / 32,7 tuntia = 11,009 astetta tunnissa. Tuntimäärä on suurempi kuin vuorokauden 24 tuntia, koska heiluri ei ole sijoitettu pohjoisnavalle.
ф = leveyspiirit päiväntasaajalta pohjoiseen ja etelään
ω = 360 sin ф /päivä
ω = 360 x sin *48.84625°
ω = 271°
=>
ω = 271° / 24 tuntia
ω = 11,294° (31,88 tuntia)
Kaava ei ole tarkka, sillä siitä puuttuu kitka (aikadilaatio) 1,03. Ikiliikkujaksi ei ole näinkään yksinkertainen laite, jonka koe samalla osoitti.
(32.7 tuntia/31.88 tuntia = 1.03) = aikadilaatio
Foucaultin koe tarkemmin laskettavaksi esimerkiksi.
ω = 360 sin ф /päivä / 1,03
ω = 360 x sin *48.84625° / 1,03
ω = 263,1657°
=>
ω = 263,1657° / 24 Hrs
ω = 10,96° (32,85 tuntia )
(748)
*48.84625° Sijainti valokuvasta
20. Luonnollinen kävelyvauhti
Kaikilla eläimillä on niiden luonnollinen kävelyvauhti, ihminen tähän mukaan lukien. Yksi jalan heilahduksen jakso, on täysi edestakainen heilahdus. Jos jalan pituus on 98 cm. Paljonko aikaa kuluu jalan heilahduksen liikkeeseen (askelpariin = S = 2 x 75 cm)? Askeleen pituus 75 cm on mitattu kävellessä tai ne voivat olla maahan jääneitä jälkiä. Näin dinosaurusten kävelynopeuden voi määrittää jälkikäteen. Eikä ainoastaan dinosaurusten kävelynopeuden. Ymmärrämme matkan ja nopeuden liittyvän ajan käsitteeseen. Pituus on määritettävää yksinkertaisella mittanauhalla ja etäisyys käyttäen jotakin yksikköä kuten maili tai kilometri. Laskemalla pääsemme syvemmälle ajan käsitteeseen, kuin kelloa tarkastemalla. Tuotteilla ovat samat lainalaisuudet aikaan, kuin kaikilla muillakin
20.1 Fysikaalinen heiluri
T = 2 x Pi x SQRT (2 L / 3 g)
T = 2 x Pi x SQRT (2 x 0,98 / (3 x 9,8))
T = 1,62 sec Kultainen leikkaus 1,618
T = Aika s g = 9,8 m/s2 L = 0,98 m Pi = 3,14...
20.2 Kävelyvauhti
v = S / T
v = 1,50 m / 1,62 sec = 0,80 m/s = 3,3 km/h
v = Nopeus m/s S = Yhden jakson pituus
Moni sanoo pystyvänsä kävelemään kuusi kilometriä tunnissa. Kenties hetken, mutta ei kauan. Tämä, sillä on olemassa suhteellisuus jalan pituuden ja painovoiman kesken. (747)
21. Jarrutusmatka fysiikassa
Fysiikassa kitka lasketaan usein periaatteen ymmärtämiseksi jarrutustapahtumana autolla. Tässä yhteydessä kertomatta jää, ettei kitkaan perustuvaa pysähtymismatkaa pysty laskemaan. Rengaskokeet tehdään käytännön kokeina uusille renkaille ajoneuvoilla. Oletuksena autot pysähtyvät yhtä pitkällä jarrutusmatkalla, mutta se ei pidä paikkaansa. Joissakin autoissa on ABS-jarrut, ajonvakausjärjestelmä, painoerot kuormituksen jakautumisessa. Suomessa asfaltti on keväällä erittäin karheaa, pinnan loppukesästä tasaannuttua. Lisäksi kokeissa saadut jarrutusmatkat ovat useiden jarrutusten keskiarvo ja tuloksista voidaan jättää huonoimmat jarrutukset pois. Mikä näistä on sinun jarrutustapahtuma paniikkitilanteessa? Fysiikassa jarrutusmatkan laskenta ei myöskään ota kantaa reaktioaikaan eri nopeuksilla. Lisäksi kitkaan perustuvia laskelmia tehdään äärettömän jäykille kappaleille. Tätä auto joustavine jousituksineen ja renkaineen ei ole. Käytännössä tien pintakaan ei ole joka kohdassa samanlainen. Tuntemattomien muuttujien määrä on tästä johtuen suuri. Rengastestit tehdään talvisin merkistä jarruttaen kuivalla jäällä, kesärenkaille kuivalla asfaltilla. Olosuhteet, joissa joudut jarruttamaan, voivat oleellisesti poiketa testeissä kirjoitetusta ammattikuljettajien tekemänä.
Jarrutusmatka on suoraan verrannollinen nopeuden neliöön (v2) ja kääntäen verrannollinen tien pinnan ja renkaiden väliseen kitkakertoimeen.
S = jarrutusmatka v = alkunopeus m/s μ = kitkakerroin g = 9,81 m/s2
S = v2 / (2 x μ x g)
Wf = työkitka m = massa
Wf = μ x m x g x s = 0,5 x m x v2
Kitka
Lepo Liike
Märkä asfaltti 0.6 0,5
Kuiva afaltti 0,8 0.7
Märkä jää 0,1 0,8
Kuiva jää 0,2 0,15
Kuivalla tiellä auton 10 kN (1000 kg) ajonopeus on 100 km/h (27,77 m/s), jolloin taulukko antaa kuivan asfaltin kitkakertoimeksi 0,8. Tästä laskemalla saadaan jarrutusmatkaksi noin 49 metriä. Testit lukitsemalla jarrut tai lukitsematta jarruja jarruttaessa, ovat osoittaneet, että kovalla tasaisella pinnalla jarrutusmatkat ovat jokseenkin yhtä pitkät.
S = 27.782 /(2 x 0,8 x 9,82) m
S = 49 m
Wf = μ x m x g x s = 0,5 x m x v2
Wf = 0,8 x 10 000 N x 9,82 m/s2 x 49 m/s = 0,5 x 10 000 N x 27,772 m/s
Wf = 3849 kNm/s = 3858 kNm/s
Tämän jälkeen tullaan siihen, joka harvoin otetaan huomioon. Laskettaessa pysähtymismatkaa, kitkakerroin 0,8 on nimellinen lepokitka. Taulukoidut arvot ovat hyville renkaille ja hyvälle tien pinnalle. Kitka on erittäin paljon alhaisempi märällä, jäisellä, liukkaalla, hiekkaisella, likaisella tasaisella tai öljyisellä pinnalla. Normaalisti ajetuille kuluneille renkaille, valitaan pienempi arvo 0,7 tai 0,6. Olosuhteista riippuen huonokuntoiset renkaat saattavat vaatia jopa kitkakertoimen arvon 0.5 tai 0,4.
Jarrutusmatka 100km/h nopeudella on 49 m. Mikä on jarrutusmatka 50km/h nopeudella?
49/x = (100/50)2
(1002) x = (502) * 49
10 000 x = 122 500
x=122 500/10 000
x= 12,25 m
Tarkistus
S = 13.882 /(2 x 0,8 x 9,82) m
S = 12,26 m
Suhdelaskenta ei ole yhtälöitä, mutta edellinen esimerkki selvittää suhdelaskennan periaatetta. Yleisesti yhden arvoparin tuntemalla, muuta arvoparit ovat tunnetut. Suhdelaskenta on edellisestä poikkeavsti, usein alueella, jonne yhtälöt eivät ylety. Jarrutustilanne ei vastaa kaavalla laskettua, kuten Foucaultin heilurin kaava ei vastaa todellista tilannetta. Fysiikka on hyvä, mutta sen tarkkuus ei usein kosketa elämässä tapahtuvaa. Ottakaa edes kaskovakuutus autoon, jos jarruttaminen ei muuten kiinnosta :) (989)
30. Auton pysähtymismatka
Ylemmässä kuvassa juhannusaaton "mehumatka" jatkui ojaan kotipihaan kääntymisessä. Alemmassa kuvassa oletettu satasen nopeus pysähtyi rajusti liikennemerkki pylvääseen. Pylväiden jäykkyydestä on ollut arvostelua. Onko tärkeämpää, ihmishengen säilyminen vai tolpan kestäminen? Saadessani päättää, poistaisin joustamattomat rakenteet teiden varsilta. Ylemmässä kuvassa jarrutus alkoi ensin kuivan asfaltin päältä, jossa oli hiekkaa ja jatkui soratieltä ojaan. Pysähtymismatka 50 km tuntinopeudesta noin 40 metriä omin silmin nähtynä. Alemmassa kuvassa pysähtymismatka auton rungolle alle viisi metriä. Moottori ja vaihteisto jatkoivat matkaa 40 - 50 m. Tolpassa ei ole minkäänlaista vioittumaa, eikä Ihmishenkiä lehdestä luetun perusteella menetetty. Nämä kaksi pysähtymismatkaa eivät luonnollisesti ole laskettavia, josta siirrymme laskettavaan.
Pysähtymismatka muodostuu reaktioajasta ja jarrutusmatkasta. Sopivana laskennallisena reaktioaikana pidetään yhtä sekunttia.
S = jarrutusmatka v = alkunopeus m/s μ = kitkakerroin 0.8 g = 9,81 m/s2
S = v2 / (2 x μ x g)
Jarrutus kuivalla ja puhtaalla asfaltilla
Nopeus Reaktioaika Jarrutus Yht.
km/h m m m
30 8,33 4,42 12,8 Tunnettu tieto 13 m
40 11,1 7,9 19,0
50 13,9 12,3 26,2
63 17.5 19,5 37,0
80 22.2 31.4 53,6
100 27,8 49,2 77,0
120 33,3 70,6 103,9
125 34.7 76,6 111,3
31. Auton pysähtymismatka logaritmisesti
Uskallan väittää, ettei tätä lähestymistapaa ole muualla esitetty. Pysähtymismatka muodostuu reaktioajasta ja jarrutusmatkasta. Sopivana laskennallisena reaktioaikana pidetään yhtä sekunttia. Näillä tiedoilla on laskettu alla oleva taulukko. Taulukon arvot ovat useiden jarrutusten keskiarvo, joten varaudu liikenteessä tuloksista huonoimpaan.
S = jarrutusmatka v = alkunopeus m/s μ = kitkakerroin 0.8 g = 9,81 m/s2
S = v2 / (2 x μ x g)
Jarrutus kuivalla ja puhtaalla asfaltilla
Nopeus Reaktioaika Jarrutus Yht.
km/h m m m
30 8,33 4,42 12,8 Tunnettu tieto 13 m
40 11,1 7,9 19,0 40/(Ln pii)6 = 17,8 m
50 13,9 12,3 26,2 50/(Ln pii)5 = 25,5 m
63 17.5 19,5 37,0 63/(Ln pii)4 = 37 m
80 22.2 31.4 53,6 80/(Ln pii)3 = 53,3 m
100 27,8 49,2 77,0 100/(Ln pii)2 = 76,3 m
120 33,3 70,6 103,9 120/(Ln pii) = 104,8 m
125 34.7 76,6 111,3 125/(Ln pii) = 109,2 m
Esimerkki
Tunnettuna tietona jarrutusmatka 30 km/h nopeudella on noin 13 m. Mikä on ollut suurin piirtein auton nopeus, josta on jäänyt 71 m pitkä jarrutusjälki?
30 / x = (13/71)2
(132) x = (712) * 30
169 x = 330750
x=330750/169
x= 130 km/h
Tarkistus
S = 36.112 /(2 x 0,8 x 9,81) m (130 km/h = 36,11 m/s)
S = 83 m
Taulukon perusteella, ajoneuvon nopeus on ollut 120 -130 km/h. Moottoritiellä ajoneuvon nopeus on ollut rajoitusten puitteissa. Tarkempaa tietoa auton jättämistä jarrutusjäljistä ei voi päätellä. (1002)
32. Teräksen yksikköympyrä ja alumiini (aikadilaatio)
Laskennan materiaali on teräs. Alkuräjähdyksen yhteydessä syntynyt alkumetalli, sisältäen laskennan perustan.
Steel unit circle; diameter one unit and length one unit
a) raudan ominaispaino on 7,87 g/cm3.
b) teräs on rautaa, josta on poistettu hiiltä. Hiiltä on muutama prosentti, jolloin ominaispainon arvo 7,87 g/cm3 on toimiva.
Teräksen ominaispaino ja yksikköympyrän pinta-ala ovat määritettäviä kertoimen 1,618 avulla luvusta 1.
6,181 x 1,618 = 10 = 0,6181 x 1,618 = 1
Yksiköillä laskennassa ei ole merkitystä, niiden ollessa ihmisten keksimiä. Tässä tapauksessa ohjelma laski painon grammoina, jolloin ajatellaan luvut arvoiksi 0,6181 ja 1. Tämä on samalla hyvä harjoitus arvoihin. Laskettavan ei tarvitse olla terästä. Laskemme alumiinisen levypalan painon teräksen ominaispainon perusteella. Alumiinin ominaispaino on 2,7 g/cm3.
1,618 / 0,618 x 1,034 = 2,70
Gravitaation 9,82 m/s2 kautta
1,618 /(0,618 x 9,82) x 1,034 = 0,275
Käymme läpi koko matemaattisen paletin, alkaen teräksen palasta, kuten kuvassa ja lopetamme lopputuotteen arvojen muodostukseen. Tämä vaatii ainoastaan malttia ja ajattelutavan yksinkertaistamista. Kuinka välttämätöntä on laskea alumiinin paino esitetyllä tavalla, on toinen tarina. (209)
33. Johannes Kepler
Ellipsikuvaus planeettojen kiertoradoista
 Aikanaan auringon, kuun ja planeettojen oletettiin kiertävän maata täydellistä ympyrän muotoista rataa. Kepler hylkäsi pyöreät planeettojen kiertoradat, päätyen elliptiseen muotoon, kuten nykyään tiedetään. Aikanaan auringon, kuun ja planeettojen oletettiin kiertävän maata täydellistä ympyrän muotoista rataa. Kepler hylkäsi pyöreät planeettojen kiertoradat, päätyen elliptiseen muotoon, kuten nykyään tiedetään.
Kepler havaitsi laskelmiin perustaen planeettojen kiertoratojen olevan elliptisiä. Pienemmän akselin suhde pitempään akseliin on aurinkokunnassa 99 - 100 % paikkeilla. Pieni "episykli" planeettojen radoissa on näin pieni. Auringon sijainti on ellipsin polttopisteessä kiertoradan toisessa päässä. Tätä huomiota, ei aluksi haluttu hyväksyä.
Johannes Kepler, Wikipedia
Teidän ellipsienne takia menetetään liikkeiden ympyrämäisyys ja tasaisuus, mikä tuntuu minusta sitä mielettomämmältä, mitä syvällisemmin sitä pohdin. - Jos vain voisitte säilyttää täysin ympyrämäisen kiertoradan ja selittää elliptisen kiertoratanne toisella pienellä episyklillä, tilanne olisi paljon parempi. - Astronomi David Fabricius
Kuvio liittyy suhdelaskentaan
Planeettojen kiertoradat ovat elliptisiä. joissa pienemmän akselin suhde pitempään akseliin on aurinkokunnassamme 99 - 100 % paikkeilla. Pieni "episykli" planeettojen radoissa on näin pieni. Auringon sijainti on ellipsin polttopisteessä kiertoradan toisessa päissä. Eräs kuvaus suhdelaskennassa on hehkulamppu, matemaattinen aurinko maan päällä. Tämä laskenta on materian ja fysiologian kuvausta, ei astronomiaa.
Ellipsin voi piirtää usealla tavalla, tarvitsematta ymmärtää piirrettyä kuviota. Tämän jälkeen voi kysyä lähes keneltä tahansa ellipsin merkitystä, siihen saamatta vastausta. Samoin käy, kysyessä ellipsin piirtämistä kynällä. (484)
34. Näkemisen geometria fysiikkana
- Aikadilaatio
Näkemisen geometrian ei luulisi liittyvän millään tavalla fysiikkaan, siinä jossakin määrin erehtyen. Tarkastellaan kahta yksinkertaista geometrista kuviota, neliötä ja ympyrää aikadilaatioon liittyen. Niiden pinta-alojen suhde on samaa tarkoittavaa teräksen ominaispainoon.
The visual geometry does not think in any way associated with the physics, this to some extent, mistaking. Let us consider two simple geometric pattern, square and circle connection to time dilation. Their area ratio is the same meaning to the specific gravity of steel.
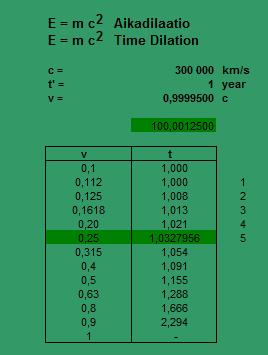
1 / (1.25 x 1.03) = 0.78
35. Teräsköyden tuotesarjan muodostuminen
- Aikadilaatio
Tarkastelemme teräsköyttä 6x26 Warrington-seale ja havaitsemme, ettei käyttäytyminen ilmiönä poikkea hehkulampusta.
Teräsköysi - Hehkulampun valo
Käsin kosketeltava - Käsin koskettelematon
____________________________________________________
Ulotteisuudet
Pituus - Pinta-ala - Tilavuus - Aika
Valonnopeus on pinta-ala c2

Miksi minä valitsin teräsköyden johtuu siitä, että lopetin edellisen kirjoituksen näkemisen geometrian kuvioihin. Neliön ja ympyrän pinta-alojen suhde on aikadilaation määrittämä, jolloin yksikköympyrän pinta-ala on teräksen ominaispaino. Laskenta kuvioiden kautta ei olisi mahdollista, ilman tätä yhteyttä.
1 / (1.25 x 1.03) = 0.78
35.1 Hehkulamppu

Saamme energian auringosta. Aurinkoa emme voi tarkastella, joten on luotava pienimuotoinen avaruus. Tähän tarkoitukseen otamme hehkulampun kuvassa. Valo lampussa syntyy, kun hehkulanka kuumennetaan korkeaan lämpötilaan sähkövirran avulla, kunnes lanka hehkuu. Hehkulampuilla on valon tuottamisessa huono hyötysuhde, noin 3 ... 5%, jolloin valo on lämmittämisprosessissa syntyvä kitka.
100 / 1,0328 = 96,82 %
Staattisen väsymisen kitka 1,033
35.2 Teräs
Wikipedia
Teräs on yleisnimi kaikille rautavaltaisille metalliseoksille, joita voidaan muokata valssaamalla tai takomalla. Teräksen hiilipitoisuus on 0,03–1,7 %. Tätä alhaisemman hiilipitoisuuden rautaseosta kutsutaan meltoraudaksi ja korkeamman valuraudaksi. Teräksen ominaisuudet riippuvat voimakkaasti sen rakenteesta, joka puolestaan riippuu hiilen määrästä, seosaineista sekä valmistusparametreista.

Teräs
35.3 Teräsköysi
Teräsköysi on kannattamiseen tarkoitettu. Tarkastelussa havaitsemme köyden tuotesarjan muodostuvan vastaavalla tavalla kuin edellisissä esimerkeissä. Teräsköyden arvot, ovat tarkistettavaa taulukoista.
The steel rope is intended for supporting. The analysis shows a range of the steel rope formed the same way as in the previous example. Steel Rope values are in the revised tables.
Halkaisija Paino
D mm kg/100 m
10 38,0
12 54,7 54,7/38,0 = 1,779
16 97,3 97,3/54,7 = 1,772
20 152,0 152/97,3 = 1,562
24 219,0 219/152 = 1,441
32 389,0 389/219 = 1,777
40 608,0 608/389 = 1,562
Keskiarvo = 1,649
1.618 x 1.0165 = 1,645
1 + (0.033/2) = 1.0165
10 - 12,5 - 16 - 20 - 25 - 32 - 40
Maailmankaikkeuden kaksiulotteisuuden sääntö määrittää kaksi kertaa kauempana olevan neljä kertaa suuremman. Arvoasema 10 => 16 on kaksi kertaa suurempi.
4 x 38 kg/100 m = 152 kg/100 m
16 x 38 kg/100 m = 608 kg/100 m
6x26 Warrington-Seale (langan murtolujuus 15,7 kN/cm2 )
Taulukoitu tieto
D mm kN/cm2
10 55,9
12 80,6 8,06/5,59 = 1,442
16 143,0 143/80,6 = 1,774
20 224,0 224/143 = 1,567
24 322,0 322/224 = 1,438
32 573,0 573/322 = 1,780
40 895,0 895/573 = 1,562
Yhteensä = 1,593
1.618 / 1.0165 = 1,591
1 + (0.033/2) =1.0165
Vähimmäismurtokuorma on kuormitus, joka on saavutettava tai ylitettävä vetomurto-kokeessa.
4 x 55,9 = 223,6 kN/cm2
16 x 55,9 kN/cm2 = 894,4 kN/cm2
(1,649 + 1,593) /2 = 1,62 = kultainen leikkaus 1,618
1.033 x 1,593 = 1,645
Lopuksi
Määritettäessä lampun kuvun säde suhteelliseksi arvoksi 1.
Pallomaisen kappaleen pinta-ala A = 4 Pii r2
r1 => A = 4 pii 12 = 12,56 pinta-alayksikköä
r2 => A = 4 pii 22 = 50,24 pinta-alayksikköä
r4 => A = 4 pii 42 = 200,96 pinta-alayksikköä
Kaavassa, säteen kasvaessa kaksinkertaiseksi, pinta-ala kasvaa nelinkertaiseksi. Ajateltaessa lämmön jakaantuvan tasaisesti pinta-alalle. Säteen (r) mitan kasvaessa kaksinkertaiseksi, pienenee lämpömäärä pinta-alaa kohden 1/4 osaan. Lopulta köyden tai lampun arvojen muodostus ei poikkea toisistaan. Sama koskee muutakin, niin kauan, kun kaikki on johdettavissa kaavaan E = m c c.
Huom! Aurinkovakion suuruus maan ilmakehän rajalla on 1,37 kW/m2
36. Vivun käsite
Arkhimedes
Kaksi kappaletta on tasapainossa, kun niiden etäisyys tukipisteestä on käänteisessä suhteessa niiden massaan. Kiinteän tukipisteen avulla voisi vivuta maapallon paikoiltaan. Arkhimedes ajatteli purkavansa taivaallisen planeettojen asennuksen. Seuraavassa laskennassa vipuamme ne niille kuuluville paikoilleen, samalla periaatteella kuin tuotteissa. Planeetat noudattavat saman, kuin tuotteet.

Image: Wikipedia
Vivuilla on rajallinen pituutensa, jonka jälkeen ne eivät toimi. Myöhemmin osoittautuu pituuden porrastuksen olevan viisi. Tämän jälkeen nämä taipuvat omasta painostaan.

Useat ajattelevat vipua konkreettisesti, mutta on olemassa myös aineettomia vipuvarsia, kuten on materiaa ja antimateriaa. Seuraavaksi aineeton vipuvarren, joka on Fibonaccin lukujono. Fibonaccin lukujono alkaa kuten Pascalin kolmio ja molemmissa raja tulee vastaan viidennellä porrastuksella.
0 - 1 - 1 - 2 - 3 - ( 5 -8 -13 )
Rivi 1 0
Rivi 2 0 - 1
Rivi 3 0 - 1 - 1
Rivi 4 0 - 1 - 1 - 2
Rivi 5 0 - 1 - 1 - 2 - 3
Rivi 6 0 - 1 - 2 - 3 - 5 - 8
Image: Wikipedia
Fibonaccin lukujono liittyy planeettojen tunnettuun etäisyyteen auringosta. Laskemme planeettojen sijainnin tai oikeastaan vipuamme ne.
0 - 1 - 1 - 2 - 3 - ( 5 -8 -13 )
Titius - Boden kaava ja Fibonaccin lukujono
Planeetta Etäisyys auringosta
Mercurius 0,39 α = 0,4 etäisyys/Distance ( 0)
Venus 0,72 α = 0,4 + 1 x 0,3 = 0,7 (0 +1 = 1)
Maa/Earth 1,00 α = 0,4 + 2 x 0,3 = 1,0 (0 +1 +1 = 2)
Mars 1,52 α = 0,4 + 4 x 0,3 = 1,6 (0 + 1 + 1 + 2 = 4)
Ceres 2,76 α = 0,4 + 7 x 0,3 = 2,5 (0 + 1 +1 +2 + 3 = 7)
a= suhteellinen etäisyys auringosta, kun etäisyys maahan on arvoltaan 1
Planeettojen etäisyys auringosta (a) on; 0,4 + Fibonaccin lukujonon numeroiden summa (suhteellisessa asemassa) kertaa 0,3.
Etäisyys auringosta Cerekseen on kaikkien kiviplaneettojen keskimääräinen etäisyys auringosta, joita kaikkia Ceres edustaa. Kahdeksan miljoonan kiviplaneetan keskimääräinen etäisyys voi hyvin olla lähellä arvoa 2,5 a. Koska lähestymme suhteellisuusrajaa viidennellä portaalla, tarkkuus pienenee.
Planeetat suurimpina tuotteina
Suhdelaskennassa tarkastellaan käsitteellisiä asioita punniten. Yhdistämällä punnitsemiseen nosteen käsitteen, voi punnita aineettomia ominaisuuksia. Arkhimedes ei kyennyt määrittämään onton kappaleen ominaispainoa, mutta laskenta määrittää myös "onton" ominaisuudet. Tästä esimerkki arvojen määrittäminen käyrille, joita ei ole. (688)
37. Valonnopeus painovoimaksi
Vuonna 1905 julkistettiin erikoinen suhteellisuusteoria (myös erityisenä- ja suppeana suhteellisuusteoriana tunnettu), josta parhaiten tunnetaan energian kaava. Perusidea teoriassa on kappaleen massan suuruuden riippuvan sen nopeudesta. Liikkuvalla kappaleella on enemmän massaa, kuin paikallaan olevalla vastaavalla kappaleella. Tämä merkitsee liikkeeseen liittyvän kineettisen energian muodon, kertoen energialla olevan massan.
E = m c2
Valonnopeus c on 299 792 458 metriä sekunnissa. Kappaleen nopeuden lisääntyessä noin 87 prosenttiin valon nopeudesta, on kineettisen energian massa suurempi, kuin lepomassa. Lähestyttäessä valon nopeutta ja yritettäessä kiihdyttää kappaletta, yhä suurempi osuus kiihdyttämiseen käytettävästä voimasta siirtyy massaan. Sanomme, ettei mikään voi liikkua valon nopeutta suuremmalla nopeudella. Lähellä valon nopeutta massa kasvaa äärettömäksi. Liikkuvan kappaleen massa on suhteellinen massa, koostuen lepomassasta ja liikkeen energiaan liittyvästä massasta.
Myöhemmin julkaistu yleinen suhteellisuusteoria huomioi painovoiman ja salli avaruuden laajenemisen. Nyt valon nopeuden sääntö ei päde. Kaukaiset galaksit saattoivat tämän seurauksena etääntyä valon nopeutta suuremmalla nopeudella.
Painovoima
Valonnopeus on 299 792 458 metriä sekunnissa. Muutamme valon nopeuden suhteelliseksi arvoksi 2,99792 458, jakamalla sen luvulla 108. Valon peitto C2 kerrotaan staattisen väsymisen kertoimella 1,03 kolme kertaa. Neliulotteisessa maailmassa aika on neljäs ulotteisuus. Muut ovat leveys, pituus ja korkeus.
2,99792 4582 x 1,033 = 9,82 (m/s2)
Tuloksena on painovoima maan päällä. Kerroin 9,82 on tuttu, mutta piin arvo 3,14 vielä tunnetumpi. Piin arvo on ympyrän halkaisijan ja kehän välinen suhde. Saamme suhteellisen valon nopeuden universumissa. (679)
(3,141592 x 0,982) / 1,03 = 2,995 (Virhe/Error 1:1000)
38. Painovoima
Ilman painovoimaa mikään ei taivu tai väsy kuormitettuna. Kaikki leijuisi painottomassa tilassa, eikä olisi kitkaa. Kitka käsitteenä on laajempi, kuin kitka kahden materian välissä. Kitka vaikuttaa kaikkeen ja laskemme tehtäviä maailmankaikkeuden kitkarvoa 1,03(3) käyttäen. Kenties seuraava kuvio on luolan seinälle heijastuva varjo painovoimasta, jollaisena Platon kuvasi maailmaamme.
Viisikulmio kuvaa painovoimaa g maapallolla
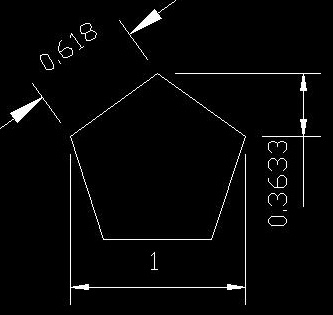
0,618 + 0,3633 = 0,9813
Arvo 0,9813 on painovoima 9,82 m/s2. Suhdelaskenta ei ole kaavoja, joten älkää miettikö desimaaleja. Miettikää, kuinka yksinkertaisella tavalla luonto esittää painovoiman. Arvon muodostuminen siirtyy esitettäviin kuvioihin, esimerkiksi täysikulma radiaaneina.
2 pii rad x 1,252 = 6,28 x 1,252 = 9,813
(605)
38.1 Gravitaatiovakio
Gravitaatiovakion määritti ensimmäisenä englantilainen Henry Cavendish vuonna 1798. Tämä oli mahdollista keksityn tarkan torsiovaa'an avulla. Samalla tarkentui maan massan suuruus Isaac Newtonin arvioon nähden. Tämä on tuttua, mutta kerrataan se suhdelaskennan näkökulmasta.
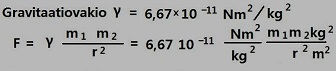
Gravitaatiovakio
38.2 Painovoima maan päällä
Maan massa m2 5,98 x 1024 kg
m1 arvon voi jättää pois tai antaa arvon 1
Maan säde 6,37 x 106 metriä
F = 6,67 x 10-11 x 5,98 x 1024 = 9,83 m/s2
(6,37 x 106)2
Painovoiman kiihtyvyyden g arvo maaan päällä (pohjolan maissa) on 9,82 m/s2. Arvo g on kappaleen kiihtyvyys sekunnin neliössä. Kaava määrittyy pinta-alaksi potenssimerkinnällä sekuntia toiseen. Pelto kasvattamiseen on käsin kosketeltavaa. Ajan peitto kiihtyvyyteen, on käsillä koskettelematonta.
Kaava antaa gravitaatiovakioksi F arvon 9,83 m/s2. Painovoiman yhteydessä käytämme arvoa, joka vaihtelee leveyspiirien mukaisesti tai meren pinnalla. Painovoima maan päällä muodostuu gravitaation vetovoimasta, josta vähennetään maapallon pyörimisestä syntyvä keskipakoisvoima. Laskenta perustuu gravitaatioon, sillä mikään ei taivu ilman painovoimaa tai väsy kitkattomana. Mikään ei pysyisi koossa, ilman puoleensa vetävää voimaa. Tästä huolimatta gravitaatio tunnetaan voimista huonoimmin. (592)
Painovoima Maan päällä
Maa vetää puoleensa voimalla, jonka aiheuttama kiihtyvyys tavallisessa päivittäisessä ympäristössä (lähellä maan pintaa) on noin g = 9,80665 m/s².

Laskettaessa aikadilaatio arvolla v = 0,979796 x c => 5
Numero viisi on tärkeä asema samaa tarkoittavassa suhdelaskennassa.
Numero viisi
Taulukon viides rivi sisältää kertoimen 0,25 x c (taulukko 1). Kahdesta veljeksestä toinen veli jää maapallolle. Toinen veljeksistä menee avaruusalukseen nopeudella 0,25 x c (c = valonnopeus 300 000 km/s²). Vuoden matkustamisen jälkeen veli on 1,033 kertaa nuorempi kuin maan pinnalle jäänyt veli (353,3 päivää vanha kalenterin mukaan)
38.3 Painovoima kuussa
 Kuun pinnalla vaikuttava painovoima on kuudesosa maan painovoimasta. Painovoimasta aiheutuva putoamiskiihtyvyys kuussa on 1,618 m/s2 eli 0,165 g. Tarkistus; 1,618 m/s2 / 0,165 = 9,81 m/s2 Kuun pinnalla vaikuttava painovoima on kuudesosa maan painovoimasta. Painovoimasta aiheutuva putoamiskiihtyvyys kuussa on 1,618 m/s2 eli 0,165 g. Tarkistus; 1,618 m/s2 / 0,165 = 9,81 m/s2
Kultainen leikkaus 1,618
Laskettaessa kiihtyvyys kuun pinnalla kuun massan ja sen halkaisijan perusteella, saadaan arvoksi 1,617 m/s2. Painovoima aiheuttaa kitkan välityksellä liikkeen pysähtymisen ja kappaleen taipumisen. Edelleen lentävän kappaleen lentorata ja tuotearvoavaruus saavat paraabelin muodon. Kuun putoamiskiihtyvyyden arvo on kultaisen leikkauksen suhdeluku 1,618.
1 1,000
1 1 1,1 x 1,0 = 1,100
1 2 1 1,1 x 1,1 = 1,210
1 3 3 1 1,1 x 1,21 = 1,331
1 4 6 4 1 1,1 x 1,331 = 1,464
1 6 1 1 6 1 1,1 x 1,4641 = 1,611 Pyöristettynä
Pascalin kolmio määrittää kuun painovoiman 1,611 m/s2, virheen ollessa 0,43 %. Kaksi desimaalia on oikein, joka ylittää suhdelaskennan tarkkuuden.
9,82 ms-2 / 6,28 rad x 1,03 = 1,611
Painovoima g / Täyskulma 2 pii radiaania x Staattisen väsymisen kerroin
Staattinen väsyminen eli universaali kitka on ikiliikkujan estävä mekaanisessa mielessä
9,82 ms-2 / 6,28 rad x 1,03(4) = 1,611
Neljä tuhannesosaa staattisen väsymisen kertoimessa muuttaa laskelmamme Pascalin kolmion arvoksi tai kultaisen leikkauksen arvoksi. Laskelmissa tämä havaitaan arvoina 1,03 - 1,033 - 1,034, sillä yksi tuhannesosa muuttaa laskelman. (797)
39. Kappaleen vapaa putoaminen
Taipumasuhde 1/1000 on kannattajan perusjäykkyys taivutuksessa, jolloin arvoja voi laskea ristiin fysiologian kanssa. Esimerkkinä 10 mm (1 cm) pyörötangon staattiset arvot. Kuvitelkaa kuvaan pyörötanko. Pyörötanko 10 mm on laskennan perustana oleva pienin pyörötanko, määrittäen muiden pyörötankojen arvot

Taipuma 1:1000 Deflection
Osana näkemisen geometriaa - as a part of Visual Geometry
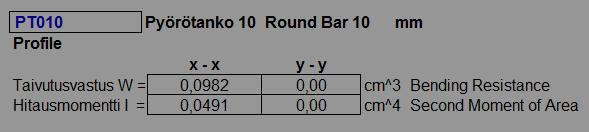
0,0982 cm x 100 = 9,82 m/s2
Painovoima maan pinnalla
0,0491 cm x 100 = 4,91 m
Vapaa putoamismatka maan pinnalla yhden sekunnin aikana
Voitte nähdä pyörötangon staattisten arvojen suhteen vapaaseen putoamiseen. Kaikki on vapaata putoamista, sen estämistä tai kitkaa putoamisen estämisestä liikkeessä. Siksi, kaikki on samaa tarkoitavaa.
Fysiikka - Fysiologia - Materia ja lujuus
Näkemisen geometriaa
50. Taipuminen yleisesti
Fysiikkaa ja fysiologiaa ymmärtämättä, ei ymmärrä taipuman olemusta. Se on vaikeaa, sillä fysiikka ei opeta taipumaa. Taipuman katsotaan liittyvän lujuuden määrittämiseen, joka kuuluu insinöörikoulutukseen. Silti, taipuma liittyy teoreettisiin oppiaineisiin, kuten se liittyy tunnetuinpaan energian kaavaan. Energian kaavojen kautta on selitettävissä myös urheiluun liittyviä kysymyksiä. Fysiologinen taipuma lisää suorituksen aikaa, jonka voi osoittaa aikadilaationa.

Yksinkertaistaen, kappaleen taipuma aiheuttaa venymän ja kutistumisen, jonka ulkoinen ilmentymä on kappaleen muodonmuutos. Tästä sanotaan kappaleen taipuvan. (678)
51. Ulotteisuudet
51.0 Nollaulotteisuus - piste
Piste, josta ei näe mitään, sillä toista pistettä ei ole. Pisteellä ei ole ulottuvuutta.
51.1 Yksiulotteisuus - viiva - pituus
Joukko pisteitä, jotka nähdään tai ei nähdä yhdessä suunnassa eteen ja taaksepäin.
I 1 = 1 = 1
I 1 1 = 2 = 1,1
I 1 2 1 = 4 = 1,21
I 1 3 3 1 = 8 =1,331
I 1 4 6 4 1 =16 = 1,4641


51.2 Kaksiulotteisuus - (poikkileikkauksen) pinta-ala - lujuus - 1,25
Litteä muoto, jossa nähdään tasona eri suuntiin
1,12 x 1,12 = 1,25

51.3 Kolmeulotteisuus - tilavuus - avaruus - 1,618
Kuution, pallon jne. muoto jossa nähdään kaikkiin suuntiin
1,25 x 1,25 x 1,0328 = 1,618
Kaksiulotteinen potenssiin kaksi x aikadilaatio 0,25

51.4 Neljäulotteisuus aika-avaruus
Aika hidastuu, massa kasvaa nopeuden lisääntyessä. Aikaa ei näe, mutta sen voi mitata.

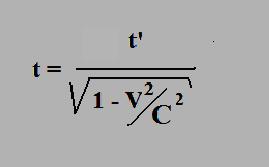
51.4 Kaartunut aika-avaruus
Tämä ylittää käsityskyvyn gravitaation ymmärtämiseksi, mutta sen voi laskea
(755)
52. Aika neljäs ulotteisuus
Ulotteisuudet
1-ulotteisuus liike etenevänä, kuten juoksu eteenpäin
2-ulotteisuus pinta-ala käsitteen kautta, voima ja vahvuus
3-ulotteisuus tilavuus
4-ulotteisuus aika, kuten Hermann Minkowski sen ymmärsi
Hermann Minkowski

Opiskelu Sveitsissä sujui Albert Einsteiniltä kohtalaisesti. Hermann Minkowskin matematiikan luennot Einstein laisti, uskoen ettei myöhemmin tarvitsisi korkeampaa matematiikkaa. Tätä hän jälkeenpäin katui.
Kun Albert Einstein algebrallisesti esitteli erityisen suhteellisuusteorian vuonna 1905, Hermann Minkowski osoitti entiselle oppilaalleen, että sen voi ymmärtää myös geometrisesti teoriana neliulotteisesta aika-avaruudesta. Myöhemmin Albert Einstein havaitsi, että geometrinen näkemys avaruusaikaan olisi tarpeen täydentämään omaa myöhempää työtä yleisenä suhteellisuusteoriana (1915). Suhteellisuuden kannalta huomattavaa on Albert Einsteinin esittäneen saman algebrallisesti, jonka Hermann Minkowski esitti geometrisesti.
Laskennan ajatus on, kuten yllä mainitussa tekstissä. Ilmiöitä voidaan tarkastella mittaamalla, laskea ja esittää geometrisesti. Kuinka laskemme kahdensadan metrin juoksun maailmanennätyksen. Tätä fysiikka ei laske?
Esimerkki yksiulotteisuudesta - Lyhyet juoksumatkat
Kuvio esittää juostavien matkojen noudattavan Pascalin kolmiota.
1 1 1 x 100 m = 100 m
2 1 1 2 x 100 m = 200 m
4 1 2 1 4 x 100 m = 400 m
8 1 3 3 1 8 x 100 m = 800 m
16 1 4 6 4 1 16 x 100 m = 1600 m (maili)
Tämä on näkemisen geometriaa nähdä lyhyet juoksumatkat
Fibonacci numerot
1 - 1 - 2 - 3 - 5 - 8 - 13 - 21 - 34 - 55 - ....
Fibonaccin lukujono alkaa 1 - 1 - 2... Pascalin kolmio alkaa saman kaltaisesti.
100 m + 100 m = 200 m
Yleisurheilun 100 m juoksu
100 m juoksun ME-aika on 9,58 s.
200 m ME - 200 m WR
2 x 9,58 sec = 19,16 s (ME 19,19 s)
100 m + 100 m = 200 m
1 - 1 - 2

Juostessa ensimmäinen 100 metriä, tapahtuu matkalla väsymistä. Toivon teidän tietävän, ettei maailmassa ole juoksijaa, joka pystyy täysillä juoksemaan sata metriä. Ilman väsymistä aika olisi oletettavasti seuraavan laskelman mukainen.
9,58 s / 1,0328 = 9,276 s.
200 metrin matkalla, kun väsyminen huomioidaan
2 x 9,276 x 1,0328 = 19,16 s
ME -tuuliolosuhteet
100 m: Tuuli / Wind + 0,9 m/s 200 m: Tuuli / Wind - 0,3 m/s
Esimerkiksi tuuli tekee eron aikaan 19,16 s = 19,19 s. Ymmärrätte, että tämä on ainoa tapa laskea tämän kaltaisia ilmiöitä kuten juoksutapahtumat. Aikadilaation kautta laskenta muodostuu osaksi fysiikkaa. Molemmat maailmanennätykset ovat Usain Boltin nimissä, joka tekee ajoista vertailtavaa. (412)
53. Kaksosparadoksi
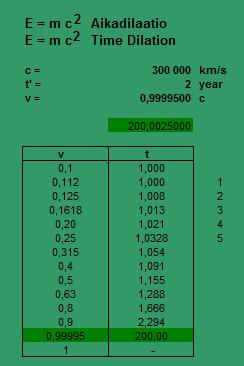 Vuonna 1911, Paul Langevin antoi esimerkin kuvaamalla tarinan matkustajasta, joka tekee matkan Lorentzin kertoimella γ = 100 (99,995% valon nopeudesta). Matkustaja pysyy vuoden ajan ammuksessa, joka sitten vaihtaa suuntaa. Palattuaan, matkailija havaitsee, että hän on vanhentunut kaksi vuotta ja 200 vuotta on kulunut maapallolla. Vuonna 1911, Paul Langevin antoi esimerkin kuvaamalla tarinan matkustajasta, joka tekee matkan Lorentzin kertoimella γ = 100 (99,995% valon nopeudesta). Matkustaja pysyy vuoden ajan ammuksessa, joka sitten vaihtaa suuntaa. Palattuaan, matkailija havaitsee, että hän on vanhentunut kaksi vuotta ja 200 vuotta on kulunut maapallolla.
Max von Laue (1911, 1913) kehitti Langevin selitystä, käyttämällä Minkowskin aika-avaruuden muodollisuutta. Hän kirjoitti, että epäsymmetrinen ikääntyminen selittyy sillä, että astronauttikaksonen matkustaa kahdessa erillisessä aikakehyksessä, kun maassa oleva kaksonen pysyy yhdessä aikakehyksessä, ja aika kiihtyvyytenä voidaan tehdä mielivaltaisen pieneksi verrattuna jatkuvaan liikkeeseen. Lopulta Herra Halsbury ja muut poistivat kiihtyvyyden ottamalla käyttöön "kolmen veljen"-lähestymistavan. Matkustava kaksonen siirtää kellonsa näyttämän kolmannelle, matkustaen vastakkaiseen suuntaan. (190)
54. Energialla on massa
Kuvattaessa ilmiöitä fysikaalisesti, tarvitaan kolmea suuretta, joita ovat aika, etäisyys ja massa. Jonkun liikkuessa suurella nopeudella tarvitaan Lorenz-muunnoksen ilmaisevat yhtälöt. Tosiasia on fysikaalisen maailman ilmiöissä, niiden lopullinen muoto osoittautuu yksinkertaiseksi kuvaukseksi.
Ajan ja etäisyyden tiedämme suhteelliseksi toisiinsa nähden. Massan suuruus vaihtelee suhteessa valon nopeuteen, joka kaavassa on pinta-ala. Nopeuden kasvaessa massa kutistuu liikkeen suunnassa, mutta leveyden ja korkeuden suhteen säilyy muuttumattomana. Massa on kyky vastustaa liiketilan muutosta, jonka Newton toi esille. Suhdelaskennan myötä akselinpätkä kätkee saman fysikaalisen lainalaisuuden, kuin ilmiöt kosmoksessa.
Newton F = a x t
Einstein E = m c2
Planck E = h v
54.1 Nopeus ja massan kasvu
Valon absoluuttinen nopeus 300 000 km/s jää hahmottamatta suuren arvonsa vuoksi. Siksi tarkastelemme valon nopeutta arvona, jonka ymmärrämme. Määritämme valon nopeudeksi 100 kilometriä tunnissa ja tarkastelemme tätä.
Kevytmoottoripyörä painaa 125 kg ja kaksi matkustajaa 125 kg, yhteismassaltaan 250 kg. Massan 250 kg, moottoripyörän 11 kW moottori kuljettaa maapallon olosuhteissa.

Moottoripyörä kiihdyttää saavuttaen 20 km nopeuden, kokonaismassa on kasvanut 1,021 -kertaiseksi (255,25 kg).
Moottoripyörän saavutettua 63 km nopeuden, kokonaismassa on kasvanut 1,288 kertaiseksi (386,4 kg).
Moottoripyörän saavutettua 90 km nopeuden, kokonaismassa on kasvanut 2,294 kertaiseksi (688,42 kg). Moottoripyörä ei jaksa nousta mäkeä.
Moottoripyörän saavutettua 99 km nopeuden, kokonaismassa on kasvanut 7,089 kertaiseksi (1772,25 kg). Valon nopeutta ei mikään ylitä, tässä tapauksessa sadan kilometrin tuntinopeutta.
Moottoripyörän polttoaineen kemiallinen energia vapautuu palamisen muodossa. Energiasta saatu teho välittyy renkaan kautta tien pintaan lisäten moottoripyörän nopeutta. Liikenopeuden kasvamisen seurauksena, moottoripyörän liikemääräenergia E kasvaa. Valonnopeus on absoluuttinen mihin tahansa nopeuteen nähden, jolloin arvo c säilyy. Jotta energiakaava säilyy, on massan suuruuden muututtava. Edellä oleva on tunnettua. (520)
55. Aikamatkailu suhteellisuuden rajoissa
 Eräänä päivänä teknologia kehittyy mittakaavaan, jolloin saavutetaan 0,9 c nopeus eli 270 000 km/s. Tämä oletuksena, mutta mitä tapahtuu matkailijan matkustettaessa vuoden kuvatulla 0,9 c valon nopeudella maahan nähden? Eräänä päivänä teknologia kehittyy mittakaavaan, jolloin saavutetaan 0,9 c nopeus eli 270 000 km/s. Tämä oletuksena, mutta mitä tapahtuu matkailijan matkustettaessa vuoden kuvatulla 0,9 c valon nopeudella maahan nähden?
Mitä maan päällä on tapahtunut tällä välin, hänen lähdettyä matkaan tammikuun ensimmäinen päivä 2043?
Laskelmasta näkee matkaajan palaavan takaisin maahan kevään kynnyksellä vuonna 2045. Oman kalenterinsa mukaan, matkaaja kokee saapuvansa uudenvuoden juhliin vuoden 2043/2044 taitteessa. Selvennykseksi niille, jotka eivät tunne ajatusta. Suurella nopeudella matkustettaessa aika liikkuvassa tilassa hidastuu lähtökohtana olevaan ajan kulkuun nähden. Esimerkissä matkaaja määrittää paluunsa takaisin maan päälle mukanaan olevan kellonsa avulla. Toisessa aikakoordinaatiossa olevat kellot maan päällä, tulevat kulkemaan kaavan mukaisen ajan 2,294 vuotta.
Ilmaus; "kellot tulevat kulkemaan kaavan mukaisen ajan", on mielenkiintoinen. Aika ei virtaa mihinkään suuntaan, vaan on paikallaan oleva samoin kuin kellojen kulkeminen ajassa. Kellon rattaiden vieriminen toisiinsa nähden määrittää ajan kulumisen, meidän samalla liukuessa ajassa yhteen suuntaan, jota sanomme eteenpäin.
21.6 2018*08:00
www.karikolehmainen.com
gr8pr0@suomi24.fi |