Tuotteet laskemalla
Laskenta johdattaa tuotteiden vertaamiseen laskemalla. Koska kaikki on samaa, laskelma esitetään toisinaan lujuuden määrittämisessä, näkemisen geometriassa, fysiologiassa ja fysiikassa.
Sisältö:
1. Tuotevertaaminen laskemalla.
2. Tuotteistettu kilpaurheilu.
3. Havainto I.
4. Tuotteen paino laskemalla.
5. Tuotearvoavaruus.
6. Ruuvikuljetin tuotteena
7. Ruuvikuljetin tuotearvoavaruudessa.
8. Eri mittayksiköt
9. Kultainen leikkaus
10. Kultainen leikkaus tänään
11. Kultainen leikkaus tuotteissa
12. Luonnon modulaarinen rakenne
13. Mittalaiteusko
14. Arvojen määrittäminen vertailumenettelynä
15. Metriset vakiomutterit
16. Painon määrittäminen
16.1 Nosto-orret 500 kg
16.2 Siltaelementit jalankulkijoille
16.3 Nostopöytäsarja 1
16.4 Nostopöytäsarja 2
17. Ruuvin tuotesarjan muodostuminen
18. Teräsköysisarjan muodostuminen
18.1 Hehkulamppu
18.2 Teräs
18.3 Teräsköysi
19. Nostokorvat teräsrakenteisiin
20. Nostokorvakkeet 500 - 40 000 kg
21. Siltanosturi 2 t, 14 m
1. Tuotevertaaminen laskemalla
Eräs laskennan mielenkiintoinen sovellus on tuotevertaaminen laskemalla. Vertaaminen tarkoittaa omien tuotteiden vertaamista keskenään tai kilpailijan tuotteeseen. Vertaamme tunnettuja tuotteita, joiden tiedot ovat todennettavaa. Lisäksi vertaamme tuotteita, joista harva tuntee menettelyn niiden vertailemiseksi. Voimme verrata myös tuotteita, joita ei ole valmistettu tai syystä tai toisesta tehdä. Tämän tarkoittaa; tuotetta ei välttämättä tarvitse valmistaa sen ominaisuuksien selville saamiseksi.

Varjot paljastavat tuotteen arvot
Voimme hyvin aloittaa laskennan kultaisen leikkauksen suhdeluvun yhteydessä ja Homo Sapiens "tuotteella". Fyysinen mitoitus ihmiselle vakioituu kultaisen leikkauksen yhteydessä ja mahdollistaa sarjatuotantona valmistettavat tuotteet. Hallitsemme tuotteen mitoituksen, mutta entä suoritusarvot yksilöiden välillä? Voiko ihmisten suorituskykyä verrata. Sen suhdelaskenta selvittää.
Auton suorituskyvyllä ymmärrämme kiihtyvyyttä, suurinta nopeutta, tehoa moottorissa jne. Suoritusarvo edustaa äärirajaa tuotteen ominaisuuksissa, jota harvoin tarvitsemme. 1-ulotteinen, etenemiseen perustuva kilpaurheilu, pyrkii löytämään ääriarvon suoritukselle. Toisaalta 3-ulotteisen tuotteen kohdalla, ei ilmoiteta tuotteen olevan tarkoitettu 500 kg kuormalle, mutta urheilutermillä "katkeavan" eli vaikkapa murtuvan 2000 kg kuormituksella. Tämä johtaisi vaaralliseen tilanteeseen, ymmärtämättä väsymisilmiötä tuotteissa.
Vertailemme tuotteita mm. Fibonaccin lukujonon 1 - 1 - 2 pohjalta. Otamme kaksi 1- ja 3-ulotteista tuotetta; ihmisen suorituskyky ja nostamisen apulaitteen kuten nosto-orren. Onko näillä yhteistä tarkastelumahdollisuutta? Kyllä, vaikka tätä ei tunnisteta. Matematiikan kautta kultainen leikkaus ei avaudu. Suhteellisuuden kautta ymmärrämme, miksi näin on käynyt. (862)
2. Tuotteistettu kilpaurheilu
Kilpaurheilu on tuotteistettu, siinä laskennan poikkeamatta käytännössä teknisistä tuotteista. Laskenta huomioi energian käytön matkan aikana, samoin energian tuoton henkilön kokoon ja painoon suhteutettuna. Laskemme myös energian käytön ihmisen ikäryhmien kunnon mukaiseksi, jolloin ihmisen koolla ei ole merkitystä. Cooperin-testi ei kysy painoa tai pituutta, vain ikää. Laskenta tuottaa yllätyksen ihmisen koon suhteen ja lihasten tehontuottoon urheilijoiden kesken. Kultainen leikkaus on tässä mukana. Voimme laskea energiana juoksumatkan, saada se aikana ikäluokalle, matkalle, kuntoryhmälle jne. Laskenta ei sisällä vilppiä mutuna uskottavaksi. Laskin kädessä päättelette johdonmukaisesti urheilun tilan. Kun yksi edellisiin liittyvistä tunnetaan, muukin on tunnettua. Kenties ette halua saada sitä selville?
Kunto on energian tuottoa, käytännössä hapenottokykykyä. Laskemme esimerkiksi juoksuasennon vaikutusta suoritukseen, vertaamalla tämä siltanosturin pääkannattajaksi. Paljonko energiaa sitoutuu taipumaan, sillä taipumisesta on kysymys huonossa juoksuasennossa ja tämän kuluttaessa energiaa.
Siltanosturin pääkannattaja ei nostossa taivu kuorman voimasta. Sen tekee vaikkapa vesivoimalan potentiaalienergiasta muunnettu sähkö, joka nostaa kuorman pääkannattajan päälle sijoitettuna nostokoneistona. Kyse on potentiaalienergiasta, joka siirtyy kimmoenergiaksi pääkannattajaan. Puhumme puristus ja vetojännityksestä näkemällä sen silmin taipumana. Emme ole laskeneet, mihin energia menee, kuinka paljon ja miksi. Rautalangan taivuttamisen käsissä tiedämme, laskematta paljonko lanka tuottaa energiaa. Lujuuslaskennassa jännitysten laskemiseen rakenteessa, käytetään usein paljon aikaa, tekemällä tämä muodonmuutosten tarkastelun kustannuksella.
Lopuksi ajatellaan metallin epäkeskopuristinta, joka taivuttaa kappaleen. Iskun kesto on sekunnin murto-osia ja taivuttamiseen tarvittu energia suurelta osin siirtyi lämmöksi taivutettuun kappaleeseen. Jäljelle jää fyysinen muoto kappaleesta, jossa jäähtymisen jälkeen on sama energian määrä, kuin ennen muodon muokkausta. Juoksijakin lopulta tuottaa vain lämpöä. Asioita voi tarkastella yksinkertaisesti, ottamalla asian kerrallaan. Laskemisessa on usein kyse parhaista tuloksista, joten maailmanennätyksiin on hyvä tutustua. (657) (657)
ME-tilastoja
Havainto I
Tuotteen tai ilmiön arvon edustaessa pistettä käyrällä. Kahden ensimmäisen pienimmän pisteen välille kokonaisuutta, piirtyy suora viiva.

Fibonacci Sequence 1 - 1 - 2
1 + 1 = 2
100 m + 100 m = 200 m
9,58 s + 9,58 s =*19,16 s
Ensimmäinen asia on määrittää pienin arvo. Kaikkien tuntema on sadan metrin juoksumatka lyhimpänä ratamatkana. Seuraava on kahdensadan metrin juoksu, jossa aika käytännössä on kaksi kertaa sadan metrin aika. Tämän näkee valokuvan kahdesta ensimäisestä kaatuvasta dominopalikasta.
Kaksi pienintä arvopistettä voi määrittää yhteenlaskun periaatteella. Tästä eteenpäin näin ei menetellä, sillä arvot olisivat suoraan määritettäviä. Kirjoissa mainitaan maailmankaikkeuden eksponentiaalisen rakenne, sitä selittämättä. Periaatteen suorasta viivasta merkitsi Fibonacci. (53)
(*200 m ME 19.19 sekuntia)
4. Tuotteen paino laskemalla
Tuotteissa minä kiinnostuin seuraamaan aluksi painon muodostumista. Pienempi tuote ei saanut painaa enemmän, kuin suurempi. Välikokoa tuotteesta ei kannata suunnitella, mikäli hyöty jää pieneksi. Aluksi havainnot olivat yleisluontoisia. Pian havaitsin saapuvani samaan monessa merkityksessä. Yritin selvittää suoraviivaisesti tuotteiden kokoja, siinä onnistumatta. Tämä vaihe jäi kertomatta muille, sillä pidin sitä turhana. Jokainen tuote ja mitoitus muodostivat ainutkertaisen laskennan, eikä niitä tullut sotkea keskenään. Tietokoneet kehittyivät nopeasti ja nämä kertoisivat pian tarvittavan tiedon tuotteista. Ajattelin saavamme tiedon sisältäviä tuotteita, ostaessamme tietokoneen. En ajatellut ostavamme tyhjiä sähköisiä laatikoita, joihin keräämämme tieto ei aina suosiolla sijoitu.
Tuolloin tuntui tärkeältä osata ulkoa peruskaavat jännitysten ja taipumien laskentaan jne. Kone-elimet olivat syöpyneet mitoituksen osalta aivoihin, jolloin oli luonnollista käyttää osia ja materiaaleja, jotka helposti olivat siirrettävissä aivojen antamien käskyjen kautta viivoiksi paperille.
Suunnittelutyö tehtiin 80-luvun alkupuolella piirustuslaudalla. Tietokone osaluetteloiden laadintaan yleistyi vuosikymmenen puolivälin jälkeen, ohjelmakielenä Basic. Tietokoneeni kykeni laskemaan viisi nauha-asemaan tallennettua ohjelmaa yhteen ja tulostamaan laskennan. Vaikka yksittäisiä ohjelmia oli laskennasta, ei kuittia muistuttavien tulostusteiden välille osannut tehdä johtopäätöksiä. Ei sellainen toisaalta tullut edes mieleen. Jokainen laskenta oli erillinen. Oliko näin vai teinkö liian hätäisen johtopäätöksen? (776)

Suhteellisuus varjojen kautta
5. Tuotearvoavaruus
Arvoavaruuden käsite syntyi omien tuotteiteni suunnittelun yhteydessä, kun käytin järjestelmällistä menettelyä tuoteperheiden suunnittelemiseksi. Suunnittelin tuotteita tietokoneen avulla 80-luvun alkupuolelta lähtien. Aluksi pienten ohjelmapätkien avulla laadituista tuotteista syntyi johdonmukainen kokonaisuus, joka yllättää vieläkin tasaisuudellaan.
Käsite tuotearvoavaruus oli välttämätön laskennan kannalta. Tämä perustui havaintoon lainalaisuudesta maailmankaikkeudessa ja tämän liittyessä myös koneenrakennukseen. Ajatus irrallisesta maailmankaikkeudesta koneenrakennuksessa, on kuolleena syntynyt ajatus. Fysiikassa voimme muuttaa arvoja eri yksiköiden välillä, suhdelaskennan jäämättä käsitteen ulkopuolelle. Vain gravitaation kohdalla, tiede on voimaton sitä selittämään. Suhdelaskenta perustuu suurelta osin gravitaatioon, silti pyrkimättä selittämään ilmiötä. Paljon sen luonteesta saa kuitenkin selville suhdelaskennan avulla.
Kokemuksen lisäksi tarvitsemme jonkin, jolla havaita tuotearvovaruudesta heijastuvan tiedon. Kehitin tähän tarkoitukseen tuotekehitysohjelmiston, joka kerää ja tuottaa tietoutta tuotesuunnitteluun. Menettely kokoaa hajallaan olevaa tietoa ja keskittää kerätyn tiedon uuden tiedon löytämiseksi. Suhdelaskenta on menettelyn esiintuoma kokonaisuus. Tuotteisiin perustuvana laskenta on tosiasia, jota ei voi kiistää. Jatkona tälle on vastaava käsittely fysiologiaan ja fysiikkaan. (220)
6. Ruuvikuljetin tuotteena
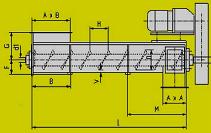 Teknisesti ruuvikuljetin on yksinkertainen ja halpa, mutta haittapuolena on kuluminen ja tehontarve kuljetettavaan materiaalin määrään suhteutettuna. Kuljettimen kapasiteetti on yleensä 5 - 40 m3/h, jolloin suurimmat voivat olla yli 200 m3/h. Suurilla materiaalin virtauksilla, muut kuljetinratkaisut tulevat usein edullisemmiksi. Teknisesti ruuvikuljetin on yksinkertainen ja halpa, mutta haittapuolena on kuluminen ja tehontarve kuljetettavaan materiaalin määrään suhteutettuna. Kuljettimen kapasiteetti on yleensä 5 - 40 m3/h, jolloin suurimmat voivat olla yli 200 m3/h. Suurilla materiaalin virtauksilla, muut kuljetinratkaisut tulevat usein edullisemmiksi.
Ruuvikuljetin tuotervoavaruuden nosteessa

Laskennan malli
Laskenta antaa mallin, kuinka kuljettimen tiedon tuntemalla, muiden kuljettimien vastaava tieto tunnetaan. Tietäessä esimerkiksi ruuvikuljettimen painon, tämä on muutettavissa muiden vastaavien kuljettimien painoksi. Tuentaväli voi kasvaa tai lyhentyä jne. Laskemme kaikki kuljettimet sarjassa ja lisäksi tarkastelemme poikkeuksia. Laskenta tarkkuus on alle 5 prosenttia.
Vaihtoehtoinen määrittämistapa
Ilman suhdelaskentaa voi laskea tehon ja kapasiteetin kuljettimille, mutta painon määrittäminen on vaikeampaa. Kuinka moni hallitsee tämän tehtävän? Suhdelaskennan avulla, kaikki hallitsevat tämän. Laskenta varmistetaan vertaamalla kuljettimien toimittajien antamiin tietoihin. Lisäksi on laadittu laskentaohjelma standardeihin ja laskentaohjeisiin perustuen, liittäen tähän kokemukset kuljettimista. Ruuvin levittäminen on myös eräs ruuvikuljettimeen liittyvä tehtävä. Opimme tavan mitoittaa ruuvin levitys oikein. Erään kirjallisuuden antama malli tekee käytännössä levyosasta väärän mittaisen. (158)
7. Ruuvikuljetin tuotearvoavaruudessa
 Kuuntelen markkinointimiestä tuotteistamisesta, jolloin korvaan osuu lause: Ensimmäisen tuotteen yhteydessä tulee jo miettiä, tuleeko malleja lisää ja mihin tuoteavaruuteen tuote sijoittuu. Kuuntelen markkinointimiestä tuotteistamisesta, jolloin korvaan osuu lause: Ensimmäisen tuotteen yhteydessä tulee jo miettiä, tuleeko malleja lisää ja mihin tuoteavaruuteen tuote sijoittuu.
Tämä on kuin suhdelaskennan johdatus, sillä tuoteavaruuksia on yhtä monta kuin on tuotteita.
Esimerkiksi ruuvikuljettimet hakkeelle ovat omassa tuoteavaruudessa, ruuvikuljettimet kiviaineksen siirtoon omassa. Tämä, sillä jälkimmäiset ovat rakenteeltaan kuluttavaan käyttöön ja vahvempia rakenteeltaan.

Kuvitellaan ruuvikuljettimen sijaitsevan tuoteavaruudessa. Siihen vaikuttaa vaikuttaa gravitaatiovoima, josta vähennetään keskipakoisvoima maapallon pyörimisestä. Jäljelle jää painovoima G 9,82 m/s2. Sekunnin neliö (m/s2) on mielenkiintoinen pinta-alan merkintä. Siitä seuraa laskennallinen noste, sillä pinta-alaan kohdistuu paine. Kuljettimen arvot nousevat laskemalla pintaan, kuten sukellusvene valokuvassa. Ajatus, jonka arkhimedes keksi, tähän päivään sijoittuvana. (124)
8. Eri mittayksiköt
1,0 - 1,25 - 1,6 - 2,0 - 2,5 - 31,15 - 4,0 - 5,0 - 6.3 - 8,0 - 10,0
1 km - 1 maili = 1,618 km
1 cm - 1 tuuma = 2,5 cm
1 tuuma - 1 maili = 63700 x 1 tuuma
Erään kerran, kerroin laskennan menettelystä eräälle insinöörille. Hän sanoi olevansa erikoistunut lujuuslaskentaan. Laskelmiani katsottuaan hän sanoi; "laskelmat eivät ole mm mitoituksella. Meille on opetettu että, laskenta tulee tehdä millimetreissä, eikä hän hallitse muita yksikköjä". Menen sanattomaksi väitteestä, pahoitellen miljoonien ihmisten puolesta, jotka eivät tätä tiedä käyttäessä tuumia ja nauloja. Voin kuvitella olevani muinaisessa Roomassa esittelemässä arabialaisia numeroita ja erikoisesti numero nollaa, joka heiltä puuttuu. Tyhjän he kuitenkin osasivat jättää väliin.
Laskenta lähtee ajatuksesta, jossa suure voi olla käyttäjän mieltämä. Näitä voi laskea keskenään, niiden muuttamatta lopputulosta. Tämän ymmärtäminen voi olla vaikeaa, mutta eri mittayksiköiden käyttö, on ymmärrettävää maailmassa. Ajatellaan aluksi kultaisen leikkauksen suhdelukua 1,618, kilometrin pituutta 1000 m ja mailin pituutta 1609 m. Laskennassa mailin ja kilometrin välille, syntyy 9 metrin virhe, joka vaikuttaa luvun kolmanteen desimaaliin. Tuuma pituutena 25 mm on laskennan suhdeluku. Tästä jatkamalla tuuma on 63700 osa mailista eli suhdeluvun 6,3 mukainen. Eri suureet eivät aiheuta ongelmaa. Voimme laskea kuten aikaisemmin ja sotkea mittoja laskentaan.
(56)
 Laskennan kannalta, mittasuhteet ovat usein yhteen laskettavia, ilman mittajärjestelmän muunnoksia. 20 mm ruuvi kertoimella 1,25 on 25 mm (käytännössä 24 mm), joka on tuuman halkaisijamitta. Laskennan kannalta, mittasuhteet ovat usein yhteen laskettavia, ilman mittajärjestelmän muunnoksia. 20 mm ruuvi kertoimella 1,25 on 25 mm (käytännössä 24 mm), joka on tuuman halkaisijamitta.
Tästä jatkaen eteenpäin kertoimella 1,25, putki 33,7 mm on 1" putki eli 1,25 x 25 mm = 31,25 mm. Laskennan kautta nämä kaksi mitoituksellista maailmaa lähentyvät toisiaan. Koska lujuudellinen mitoitus tehdään lopuksi, kohteen mitoituksen ja kuormitusolettamien varmistuttua, voidaan laskennat sekoittaa keskenään. Jos putken halkaisija ei riitä poikkileikkauspinta-alana, putken seinämän paksuutta lisätään. Seuraavaksi joutuisimme valitsemaan mitan 33,7 x 1,25 = 40 = 42 mm (putki tai ruuvi)
Poikkeavista komponenteista helpoimmin on saatavissa tuumamitoituksellisia tuotteita. Jatkoin tarkoituksella 25 mm ruuvista putkeksi, joita on saatavissa tuuma- ja metrisellä mitoituksella.
Putkissa alkuhankaluuksien jälkeen, ei ole vaikeutta. Kierteiden kohdalla on samoin ja ulkoapäin samankokoinen mutteri voi yllättää amerikkalaisessa ja japanilaisessa tuotteessa, olemalla muulla mitoituksella kuin oletimme. Itselleni kävi näin asennettuani pakoputken ja havaittuani puuttuvien muttereiden olevan UNF tai UNC -kierteellä varustetut. Arvaatte, oliko minulla sellaisia.
42 x 1,25 = 63 mm - 80 mm - 100 mm - 125 mm - 160 mm - 200 mm - 250 mm
erilaiset poikkileikkaukset materiaaleista ja komponenteista. (375)
9. Kultainen leikkaus
Golden Ratio
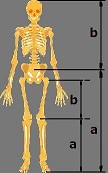 Jakamaton kokonaisuus suhteutuu suurempaan osaan samassa suhteessa, kuin tämä suhteutuu pienempään jaettuun osaan. Kultainen leikkaus on irrationaalinen vakio 1.61803398874989. Filosofiassa rationaalinen merkitsee järjen käyttöä päätöksentekoon ja irrationalisuus vastakohtaa. Jakamaton kokonaisuus suhteutuu suurempaan osaan samassa suhteessa, kuin tämä suhteutuu pienempään jaettuun osaan. Kultainen leikkaus on irrationaalinen vakio 1.61803398874989. Filosofiassa rationaalinen merkitsee järjen käyttöä päätöksentekoon ja irrationalisuus vastakohtaa.
Muita nimityksiä suhteelle ovat kultainen jako ja suhde. Laskennassa kultaisesta leikkauksesta käytetään kreikkalaista pientä kirjainta fii φ.

Golden ratio
a) Kantapäästä polveen - Kantapäästä napaan -
b) Polvesta lonkkaniveleen - Navasta pään päälle
( a + b ) / a = a / b = (fii) = 1,618 033 988
5 / 3 /1,03 = 1,618 5 > Laskennan suhteellisuusraja < 5 8 / 5 = 1,6
Kaikilla elävillä ja koneiden elimillä on tämä suhde. Kultaisen leikkauksen perusteella voi tehdä monenlaista vertailua, sillä kaikissa suhde on ennalta määritetty.
Toisin sanoen
Katkaise tanko 100 cm kahteen osaan siten, että pitempi osa on 61,8 cm. Tanko on leikattu kultaisen leikkauksen suhteessa 100 cm /61,8 cm = 1,618.
Lyhyemmän osan pituus on 38.2 cm. Kultainen leikkaus antaa nimityksenä väärän mielikuvan, kuin leikkaaminen tietyssä suhteessa. Kultainen leikkaus on materiaan liittyvä kerroin, määrittäen voimien keskinäistä suhdetta. Vaarallinen leikkaus on käsite, jonka mallintamiseen voi käyttää alla olevaa piirrosta.
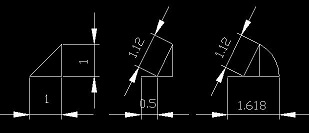
Kultainen leikkaus näkemisen geometriana
Pascalin kolmion rivien välinen kerroin 1,1, sekä lujuuslaskennan kerroin 1,12. "Katkaiseminen" voi jatkua viisi kertaa, jonka jälkeen suhteellisuusraja ylittyy. Saman voi kokeilla taittamalla paperin siististi viisi kertaa. (21)
10. Kultainen leikkaus tänään
Kultaiseen leikkaukseen on suositeltavaa tutustua Internetin välityksellä. Suuri osa avautuvista sivuista liittyy taiteelliseen sommitteluun, eräiden sivujen lähestyessä aihetta luonnon esimerkkien kautta, joita löytyy lukuisa määrä. Lopulta kaikki liittyy tavalla tai toisella kultaiseen leikkaukseen. Myöhemmin suhdelaskenta valottaa laskentaa kasveissa, vanhenemista väsymisen eri muodoissa jne. Seuraavan kerran matkustaessamme pyramideja katsomaan, tulemme tarkastelemaan niitä toisissa mietteissä. Nehän ovat myös aikansa tuotteita.

Internetin sivuilla suhdeluvun 1,618 merkitys iskostuu mieleemme. Joillakin sivuilla on kyse kaupallisuudesta, liittyen tuotteissa kultaisen leikkauksen suhteeseen 1,618. Arkkitehtuuri saa myös huomionsa valmistettujen rakennelmien kautta, alkaen Egyptin pyramideista ja jatkuen kreikkalaisen rakentamisen kautta tämän päivän tilakäsitteeseen. Silmissä kultaisen leikkauksen suhdeluvun mukainen rakennelma on sopusuhtainen, samalla todennäköisesti oikein mitoitettu. Tulen valottamaan tätä lujuuden määrittämisen yhteydessä materiassa ja tuotteissa. Internetin aineistosta saisi kirjan aikaan, annin jäädessä pintaraapaisuksi. Kultaisen leikkauksen matematiikasta on tehty maassamme vähintään kaksi yliopistollista lopputyötä. Nämä eivät muiden vastaavien lopputöiden tavoin ratkaise kultaisen leikkauksen merkitystä. Lopputyön tarkoitus, ei ole ratkaista tätä salaisuudeksi jäänyttä merkitystä. Kultainen leikkaus on kiehtonut ihmiskuntaa tuhansia vuosia. Kun siihen on tutustunut, aihe on pudottanut tarkastelijan kyydistä. Tätä samaa tarkoittava suhdelaskenta ei enää tee. (387)
11. Kultainen leikkaus tuotteissa
Kaikkialla ympärillämme vaikuttavat erilaiset mittasuhteet, josta esimerkkinä kultainen leikkaus 1,618 tuotteissa. Lisään tuotteita tälle sivulle, joista ensin kaupallinen laskin HP 12 C. Tuotteet sisältävät näkemisen geometriaa, jota ei tarvitse laskea. (821)

Hewlet Packardin 12C kaupallinen laskin sisältää suhteen 1,6125
Mitat (W x D x H)
8.0 x 1.52 x 12.9 cm
12,9 / 8,0 = 1,6125
12. Luonnon modulaarinen rakenne
Kuvittele sinisellä merkityt viivat teräsputkiksi ja rakenteen muodostavan kattoansaan puolikkaan. Putkien suhteelliset pituudet ovat 1, 1,618 ja 2,618. Putket muodostavat moduulin, jolloin rakenteen voi valmistaa kolmesta eripituisesta putkesta. Putkien väliset kulmat ovat 36, 72 ja 108 astetta eli kulman 36 astetta kerrannaisia. Lopulta 5 x 36 astetta = 180 astetta = pii() radiaania. Täyskulma 10 x 36 astetta = 360 astetta = 2 pii() radiaania = 6,28.
1,618 x 1 = 1,618 => 1,618 x 1,618 = 2,618 => 2,618 - 1 = 1,618
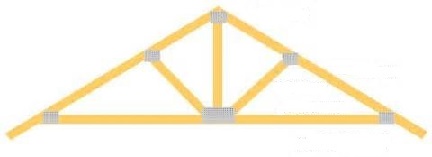
Luontoon liittyy symmetrian käsite. Vasemman puoleisen ollessa tunnettua, oikea puoli tunnetaan samassa. Ajatteletteko luonnon tekevän tukirakenteensa eritavalla, kuin me ihmiset niitä teemme? Rakenteet luonnossa näyttävät erilaisilta, mutta oletteko laskeneet niitä? Ei, ette ole, mutta kattoansas on teille tuttu. Kyllä, ne ovat tuttuja monille meistä, mutta emme ole niitä lujuuslaskeneet.
Laskennan edistyttyä, kuormitetaan ansas ja tarkastellaan voimien jakaantuminen. Vain rajoittunut mieli määrittää kuvassa olevan kattoristikoksi. Vastaavan ristikkorakenne on arvoissa ja ilmiöissä, niiden laskemisen olematta tunnettua. Samaa tarkoittavan suhdelaskennan myötä, kuviot ja kaavat tulevat samaa tarkoittaviksi. Kaikki on pinta-alaa, pituutta, tilavuutta ja aikaa. Olemme tekemisissä näkemisen geometrian kanssa. Tarkasteltaessa kuvioita, ei ole olemassa yksinkertaisempaa toimivaa mittasuhdetta kuin kultainen leikkaus 1,618. Lopulta luonnon modulaarinen ajattelu on teollisuuden hakema modulaarinen rakenne. Hyvänä esimerkkinä tästä Lego-palikat. (495)
13. Mittalaiteusko
Kerron esimerkin arkireaalisuudesta. Kesämökillä oli huono kuvanlaatu televisiossa. Isäntä pyysi antennialan liikkeen omistajaa käymään mökillään, sillä hänellä olisi erikoislaitteet antennin suuntaamiseksi. Asiantuntija saapui mökille, jolloin kysyin mittalaitteista. Hän sanoi, ettei hänellä ole mitään mittalaitetta mukana, sillä eikö antenni ja televisio ole sellaisia. Jos televisiossa on hyvä kuva, on suuntaus paikallaan. Sen hän sanoi tietävänsä, että tietyssä ilmansuunnassa on voimakas kenttä ja antenni on kohdistettava sinnepäin. Näin toimien, kuvanlaatu tuli sellaiseksi, kuin se oli mahdollista saada.
Voimme sanoa suhdelaskennan toimivan samoin. Emme välttämättä tarvitse kaavoja, voidaksemme määrittää saman, kuin kaavoilla tekisimme. Menettely on oikea ja tarkka, mikäli se kuvaa saman, kuin muulla tavalla toimimalla. (548)
Kuten televisio, laskukone kertoo selvän kuvan.
14. Arvojen määrittäminen vertailumenettelynä
Asioiden ja tapahtumien yhteydessä syntyy tilanteita, jossa tunnemme jotakin tai jonkun arvon. Tarvitsemme tiedon vastaavasta toisesta arvosta. Tätä arvoa ei tiedetä, mutta voiko tarvittavan arvon määrittää? Excell-esimerkki on laakereista, joka on tarkistettavaa tietoa laakeriluettelosta.
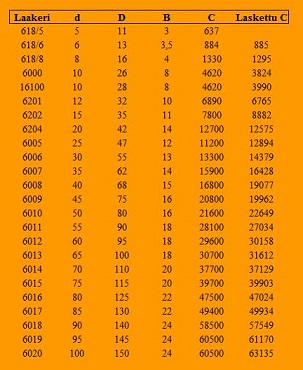
Tarkastelemme kuulalaakerisarjaa, jolloin kuulaakerista mitataan ulko- ja sisähalkaisija sekä laakerin leveys. Meillä on laakerin ulkoiset mitat, mutta ei tietoa laakerin kestoiästä. Laakerin mitat ovat kuulalaakerille 6017. Tunnemme samassa laakerisarjassa 5 mm akselille tarkoitetun laakerin dynaamisen kuormituksen C arvon. Kuinka saa määritettyä laakerin 6017 C arvon? Lähtökohta on, laakerin kestoikä on määritetty on laboratorio-oloissa. Sitä ei ole mahdollista laskemalla määrittää? Viisi vasemmanpuoleista taulukon riviä on laakerikirjasta, kuudes on laskemalla saatu arvo. Havaitaan laskemalla saadut arvot suurella tarkkuudella samoiksi arvoiksi, jotka laakerien valmistaja (SKF) on ilmoittanut.
Vertailumenettely antaa mahdollisuuden määrittää tuntemattoman arvon, tässä tapauksessa kuulalaakerin 6017 käyttöiän, kun tunnettuna on vastaava laakerisarjaan kuuluvan tuotteen tieto. Excell-esimerkissä lasketaan toisella rivillä kuulalaakerin 618/6 C arvon. Tämän jälkeen vedetään kaava taulukon alapuolella oleville riveille. Uskallan korostaa, ettei löydy laskijaa, joka muulla tavalla laskemalla saa arvon laakerista ulkomittojen kautta. Kuulalaakeriin ei näe sisälle, siinä on rasvavoitelu ja suojalevyt suojaamassa kuulia. C arvo on kokeellisella määrityksellä, sovittuja ehtoja noudattaen taulukoitu arvo. Taulukon voi laskea rivi kerrallaan edeten. Tätä voitte tarkastella avatessanne laskentasivun.
Laskennan yhteydessä kerron mahdollisuudesta määrittää tuotteita ja arvoja, joita ei ole olemassa. Kuka on sanonut laakerin 618/6 olevan maailmassa ja sitä koskaan valmistetun? Ei sitä tarvitsekaan tietää. Laskennan esimerkeissä tosin, ovat koot olemassa ja löytyvät varmistamaan kirjoittamani.
Kenties tämän kaltainen eleganssi asioiden ja arvojen yhteydessä oli Albert Einsteinin halu löytää kokonaisvaltaisempi maailmankaikkeuden selitys. Emme sitä tiedä, mutta ajattelen hänen havainneen vastaavan kaltaisen hahmottamisen, jota laskenta esittää. Esitän tässä laskennan laakereille ja myöhemmin, miten se soveltuu muuhun laskentaan.
Klikkaa taulukkoa laskentasivun avaamiseksi
15. Metriset vakiomutterit
0,8 - 1,0 - 1,1(2) - 125
Mutterin mitat voi laskea suhdelaskentana.
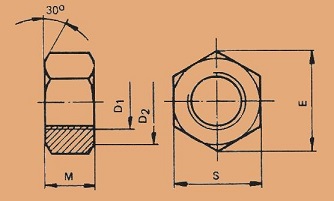
S E M
M3 5,5 6,08 1,11 x 5,5 = 6,11 2,4 0,8 x 3,0 = 2,4
M4 7,0 7,74 1,11 x 7,0 = 7,77 3,2 0,8 x 4,0 = 3,2
M5 8,0 8,87 1,11 x 8,0 = 8,86 4,0 0,8 x 5,0 = 4,0
M6 10 11,05 1,11 x 10 = 11,20 5,0 0,8 x 6,0 = 4,8
M8 13 14,38 1,11 x 13 = 14,43 6.5 0,8 x 8,0 = 6,4
M10 17 18,90 1,11 x 17 = 18,87 8,0 0,8 x 10 = 8,0
M12 19 21,10 1,11 x 19 = 21,09 10,0 0,8 x 12 = 9,6
M16 24 26,75 1,11 x 24 = 26,64 13,0 0,8 x 16 = 12,8
M20 30 33,53 1,11 x 30 = 33,30 16,0 0,8 x 20 = 16,0
M24 36 39,98 1,11 x 36 = 39,96 19,0 0,8 x 24 = 19,2
174,56 174,36
Ajatus siitä, kuinka lähes minkä tahansa voi laskea suhteellisuuden kautta, kun tietää menettelyn laskennan suorittamiseksi. Tästä syystä tulee tuntea fysiikka, lujuuslaskenta ja pitää mieli avoimena. Entä ruuvin M39 mitat, jos tunnemme ruuvin M3 mitat?
S E M
M3 5,5 6,08 1,11 x 5,5 = 6,11 2,4 0,8 x 3,0 = 2,4
M39 60 69,3 31 0,8 x 39 = 31,2
1,2511x 55 = 64
1,2511 x 6,08 = 70,8
1,2511 x 2,4 = 27,9
Porrastukset
... M24 - M30 - M39
9. 10. 11.
16. Painon määritykset
16.1 Nosto-orret 500 kg
Fibonaccin lukujono
1 - 1 - 2
Paino 1 m = 13 kg - Paino 2 m = 25 kg
Pienin tuote 1 metrin koukkuvälillä, määrittää kaksi kertaa pitemmällä koukkuvälillä olevan tuotteen painon. Tämä on sama kuin 100 ja 200 metrin matkalla juostava aika. Pienin määrittää suuremman. Tällä kertaa nosto-orret noudattivat sääntöä. Taloudellinen valmistus voi silti edellyttää toista konstruktiota, jolloin toinen tuote painaa enemmän. Tarkastelemme tätä erään valmistajan tuoteluettelon tietoihin verraten.
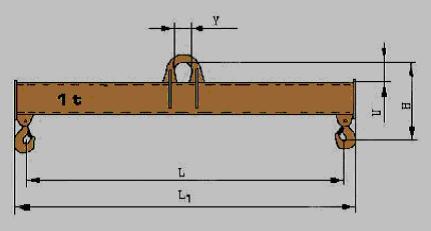
1 + 1 = 2 => 13 kg + 13 kg = 26 kg ero 1 kg = 4 %.
Prosentteina ero tuntuu suurelta, mutta on pienempi, kuin olemme kyenneet laskemaan. Paino 1 kg merkitsee euron materiaalikustannusta tuotteessa. Tarkemmin painon muodostus selitetään jäljempänä. Esimerkki kuvaa menettelyä tuotteissa ja tarkkuutta, jonka laskenta voi saavuttaa. Tuotteen paino on laskettu materiaalitietojen perusteella. Yhtä hyvin voi sanoa tuotteen olevan 26 kg, kuin painoltaan 25 kg. Tämä varsinkin, mikäli runkoputken pituus ja ainepaksuus on + toleranssissa, kuten se todellisuudessa on. Suhteellisuus tulee ymmärtää laajana kokonaisvaltaisena näkemyksenä tuotteiden painon ja arvojen muodostuksesta. Esimerkki nosto-orresta osoittaa painon olevan laskennan tarkkuuden rajoissa tai voi olla tarkka tuotteen paino. (16)
16.2 Siltaelementit jalankulkijoillle
Siltaelementit ovat yksinkertainen tapa johdattaa jalankulkuliikenne avoimien kaivantojen ylitse kunnallisteknisissä töissä. Nämä ovat oikeita tuotteita ja ovat laajalti käytössä Etelä-Suomessa. Laskemme siltaelementien painot suhdelaskennan menettelynä, joka on yksinkertaista hahmottaa mielessä. Näin ei ole aina, mutta silti kaikki noudattaa luonnonlakeja. On hyvä aloittaa helposta ja siirtyä näistä vaikeampaan.

Malli 3141 3142 3147 3148
Kaivannon leveys 1,2 - 1,5 m 2,0 - 2,5 m 3,4 - 3,8 m 4,2 - 4,6 m
Leveys kulkutasolla 1220 mm 1220 mm 1220 mm 1220 mm
Kokonaispituus 2440 mm 3660 mm 4880 mm 6100 mm
Kokonaiskorkeus 1043 mm 1063 mm 1063 mm 1063 mm
Paino 170 kg 275 kg 380 kg 490 kg
3142
1,5 x 170 kg x 1,1(2) = 286 kg 1,5 x 2440 mm = 3660 mm 4.00 %
3147
2 x 170 x 1,1(2) kg = 381 kg 2,0 x 2440 mm = 4880 mm 0,26 %
3148
2,5 x 170 x 1,1(2) kg = 476 kg 2,5 x 2440 mm = 6100 mm 2,85 %
Keskiarvo 2,37 %
Taulukossa on paino lyhimmästä siltaelementistä. Haluamme tietää muiden siltaelementtien painot, laskemalla nämä suhdelaskennan menettelynä. Arvot eivät ole näkyvää, jotka on määritetty ensimmäiselle tuotteelle. Tästä syystä tuotteiden painot on punnittu. Tämän jälkeen havaitaan ensimmäisen tuote määritti muitten painon. Pascalin kolmion rivikerroin 1,1(2) ei yllätä laskennassa.
1
1 1
1 2 1
1 ....jne
16.3 Nostopöytäsarja 1

Yritys valmistaa nostopöytiä, joilla ei ole tekemistä kuvan pöydän kanssa. Laskemme nostopöydät 1000 - 3000 kg, jossa pöydän koko pysyy samana tuotesarjassa.
Tarkastelemme pöytäsarjan painon muodostumisen suhdelaskentana. Näemme kuinka tuotesarja muodostaa painon.
Pascalin kolmio ja tehtävän ratkaisu
Nostokapasiteetiltaan 1 000 kg nostopöydän painoksi yritys ilmoittaa 185 kg ja 3 000 kg pöydän painoksi 265 kg. Välikokojen painoa ei ole tarpeen ilmoittaa valmistajan tuotteista, sillä ne tulevat esiin laskelmasta.
Nostokyky kg Paino kg Laskettu paino kg
1 000 185 Tunnettu lähtöarvo - the known weight
1 250 - 1,08 x 185 = 200
1 600 - 1,08 x 192 = 216
2 000 - 1,08 x 205 = 233
2 500 - 1,08 x 219 = 252
3000 265 -
3 150 - 1,08 x 252 = 272
Voimme olettaa laadun ja turvallisuuden säilyneen samalla tasolla
Nostolaitteissa ja noston apulaitteissa usein merkitty nostokapasiteetti on 3 200kg. Nyt jää arvattavaksi onko nostopöydän merkintä 3 000 kg tekninen merkintä pyöreänä lukuna tai perustuuko se lujuuden mukaan määritettyyn. Käytännössä 7 kg eli 3 % ero painossa ei merkitse mitään. Olemme tutustuneet Pascalin kolmioon ja siinä viiden porrasaskeleen määrään. Nyt tehdyssä tarkastelussa on kuusi porrasta, jolloin havaitsemme olevamme edelleen suhteellisuuden kannalta tarkasteltavassa tarkkuusluokassa. Entä kuinka kerroin 1,08 on muodostunut, joka esiintyy monessa yhteydessä.
1
1 1
1 2 1
Rivien välinen kerroin 1,1
1,1 merkitsee kuorman etenemän kerrointa 1,25 => 1 000 kg - 1 250 kg - jne.
1,1 x 1,1 x 1,03(4) = 1,25.
Staattisen väsymisen kerroin(1,03) pienentää eksponentiaalista painon kasvamista
1,03 => 1,12 / 1,03(4) = 1,08
16.4 Nostopöytäsarja 2
Tiedetään 1 000 kg nostopöydän painavan 185 kg, jossa pöytätason suuruus on 80 x 135 cm. Nostokorkeus pöydälle on 82 cm. Tehtävä on määrittää pöytäkoko 100 cm x 200 cm paino nostokyvyllä 2 000 kg. Valmistaja ilmoittaa painoksi 350 kg ja nostokorkeudeksi 110 cm.
Laskenta

Pascalin kolmion rivien välinen kerroin on 1,1 jonka käyttöä on esitetty riittävästi.
Laskemme tehtävän aluksi eritellen, myöhemmin voimme tehdä laskelman rivitietona, josta esitän mallin.
1,1 = 1,25
1 - 1,25 - 1,6 - 2,0
Nostokyky Paino kg Laskemalla paino
kg kg kg
1 000 185 Tunnettu paino tuotteessa
1 250 - 1,08 x 185 = 200
1 600 - 1,08 x 192 = 216
2 000 - 1,08 x 205 = 233 Nostokorkeus 82 cm
Lifting height 82 cm
1. Laskimme painon 233 kg pöydän koolle 80 x 135 cm, kun nostokyky 2000 kg. Laskettu paino on toistaiseksi vielä nostokorkeudelle 82 cm ja pöydän koko on lähtötiedon kokoinen.
16.4.1 Pöydän pituuden kerroin
Pöydän pituus 135 cm kasvaa pituudeksi 200 cm, eli arvosta 1,25 (135 cm) arvoon 2 (200 cm) = 1,12 = 1,21.
125 - 160 - 200
1 x 1,1 x 1,1
1,21
_
16.4.2. Pöydän leveyden kerroin
Pöydän leveys kasvatetaan arvosta 0,8 (82 cm) arvoon 1 (102 cm) = 1,1
1,25 x 82 cm = 102 cm
1 x 1,1
_
16.4.3. Pöydän korkeammalle nousemisen kerroin
Pöytä nousee 1,34 kertaa korkeammalle => kerroin 1,1 * 1,03 = 1,166
Tuotteen paino ei luonnollisestikaan kasva nostokorkeuden suhteena.
110 cm / 82 cm = 1,34
82 cm => 102,5 cm = 1,25 = 1,1
102,5 cm => 110 cm = 1,07 = 1,03
Laskettu kertoimet 1,1 ja 1,03 pöydän nostokorkeudelle 110 cm.
Loppupäätelmä
Neljä mittaa kasvaa kertoimella 1,1 ja lisäksi nostokorkeudesta kerroin 1,03
185 kg x 1,083 x 1,14 x 1,03 = 351 kg
Oletetaan laadun ja turvallisuuden säilyneen samalla tasolla kummassakin pöytäkoossa. (464)
17. Ruuvin tuotesarjan muodostuminen
Metrisiset ruuvit
Tunnetaan ruuvit M4 ja M5. Tästä voi päätellä, ruuvin koon kasvavan 5/4 = 1,25 eli kertoimella 1,25. Käytännössä M20 on suurin ruuvi, jota käytetään, jolloin tästä suuremmat ruuvit poikkeavat hieman mitoitukseltaan, sillä olematta suurta merkitystä.
1,25 x 1,25 x 1,03 = 1,618 = kultaisen leikkauksen suhde
4 - 5 - 6(,3) - 8 - 10 - 12(,5) - 16 - 20 - 25
1,25 x 4 = 5 mm
1,25 x 5 = 6 mm
1,25 x 6,3 = 8 mm
1,25 x 8 = 10 mm
1,25 x 10 = 12 mm
1,25 x 12,5 = 16 mm
1,25 x 16 = 20 mm
Kultainen leikkaus 1,618
4 mm ruuvi: 4 x 4 = 16
5 mm ruuvi: 5 x 5 = 25 => 25 / 16 = 1,6(18)
8 mm ruuvi: 8 x 8 = 64
10 mm ruuvi/screw: 10 x 10 = 100 => 100/64 = 1,57 x 1,03 = 1,6(18)
16 mm ruuvi: 16 x 16 = 256
20 mm ruuvi: 20 x 20 = 400 => 400 / 256 = 1,57 x 1,03 = 1,6(18)
Seuraavat laskennalliset ruuvikoot ovat M25, M32 ja M40. Käytännössä vastaavat ruuvikoot ovat M24, M33 ja M42. Näistä M33 ruuvia ei suosita, vaikka ruuveja onkin edelleen saatavissa. Myöskään M40 ruuvikokoa ei ole, vaan se on M42. Tähän on syynsä, jota määritetä tässä.
Laadun ominaisuuksia ovat tuotteen käytettävyys ja turvallisuus. Havaitsemme ruuvien kokojen noudattavan kultaisen leikkauksen suhdelukua, joka takaa turvallisuuden. Laskettaessa jännitykset, havaitaan niiden olevan samalla tasolla kaikkien ruuvikokojen osalta.
0,785 x1,25 x 1,03 = 1
0,785 neliön ja ympyrän poikkileikkauksen pinta-alojen suhde
0,785 on teräksen ominaispaino
Laskimme ruuvien koon muodostumisen & lujuuden mudostumisen tuotteessa. Kuten kaikki ilmiöt ovat johdettavissa yksinkertaisesta kaavasta E = m c c, tuotteet määrittyvät yksinkertaisen tuotteesta, kuten ruuvi. Tarvitsee kuitenkin hahmottaa monta asiaa ennen tätä. Kirjoitan tästä sivuilllani. (707)
18. Teräsköysisarjan muodostuminen
Tarkastelemme teräsköyttä 6x26 Warrington-seale ja havaitsemme, ettei käyttäytyminen ilmiönä poikkea hehkulampusta.
Teräsköysi - Hehkulampun valo
Käsin kosketeltava - Käsin koskettelematon
____________________________________________________
Ulotteisuudet
Pituus - Pinta-ala - Tilavuus - Aika
Valon nopeus on pinta-ala c2
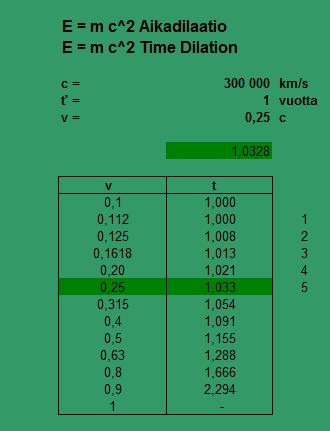
Miksi minä valitsin tällä kertaa teräsköyden, tämä johtuu siitä, että lopetin edellisen kirjoituksen näkemisen geometrian kuvioihin. Neliön ja ympyrän pinta-alojen suhde on aikadilaation määrittämä, jolloin yksikköympyrän pinta-ala on teräksen ominaispaino. Laskenta kuvioiden kautta ei olisi mahdollista, ilman tätä yhteyttä.
1 / (1.25 x 1.03) = 0.78
18.1 Hehkulamppu

Saamme energian auringosta. Aurinkoa emme voi tarkastella, joten on luotava pienimuotoinen avaruus. Tähän tarkoitukseen otamme hehkulampun kuvassa. Valo lampussa syntyy, kun hehkulanka kuumennetaan korkeaan lämpötilaan sähkövirran avulla, kunnes lanka hehkuu. Hehkulampuilla on valon tuottamisessa huono hyötysuhde, noin 3 ... 5%, jolloin valo on lämmittämisprosessissa syntyvä kitka.
100 / 1,0328 = 96,82 %
Staattisen väsymisen kitka 1,033
18.2 Teräs
Wikipedia
Teräs on yleisnimi kaikille rautavaltaisille metalliseoksille, joita voidaan muokata valssaamalla tai takomalla. Teräksen hiilipitoisuus on 0,03–1,7 %. Tätä alhaisemman hiilipitoisuuden rautaseosta kutsutaan meltoraudaksi ja korkeamman valuraudaksi. Teräksen ominaisuudet riippuvat voimakkaasti sen rakenteesta, joka puolestaan riippuu hiilen määrästä, seosaineista sekä valmistusparametreista.
18.3 Teräsköysi
Teräsköysi on kannattamiseen tarkoitettu. Tarkastelussa havaitsemme köyden tuotesarjan muodostuvan vastaavalla tavalla kuin edellisissä esimerkeissä. Teräsköyden arvot, ovat tarkistettavaa taulukoista.
The steel rope is intended for supporting. The analysis shows a range of the steel rope formed the same way as in the previous example. Steel Rope values are in the revised tables.
Halkaisija Paino
D mm kg/100 m
10 38,0
12 54,7 54,7/38,0 = 1,779
16 97,3 97,3/54,7 = 1,772
20 152,0 152/97,3 = 1,562
24 219,0 219/152 = 1,441
32 389,0 389/219 = 1,777
40 608,0 608/389 = 1,562
Keskiarvo = 1,649
1.618 x 1.0165 = 1,645
1 + (0.033/2) = 1.0165
10 - 12,5 - 16 - 20 - 25 - 32 - 40
Maailmankaikkeuden kaksiulotteisuuden sääntö määrittää kaksi kertaa kauempana olevan neljä kertaa suuremman. Arvoasema 10 => 16 on kaksi kertaa suurempi.
4 x 38 kg/100 m = 152 kg/100 m
16 x 38 kg/100 m = 608 kg/100 m
6x26 Warrington-Seale (langan murtolujuus 15,7 kN/cm2 )
Taulukoitu tieto
D mm kN/cm2
10 55,9
12 80,6 8,06/5,59 = 1,442
16 143,0 143/80,6 = 1,774
20 224,0 224/143 = 1,567
24 322,0 322/224 = 1,438
32 573,0 573/322 = 1,780
40 895,0 895/573 = 1,562
Yhteensä = 1,593
1.618 / 1.0165 = 1,591
1 + (0.033/2) =1.0165
Vähimmäismurtokuorma on kuormitus, joka on saavutettava tai ylitettävä vetomurto-kokeessa.
4 x 55,9 = 223,6 kN/cm2
16 x 55,9 kN/cm2 = 894,4 kN/cm2
(1,649 + 1,593) /2 = 1,62 = kultainen leikkaus 1,618
1.033 x 1,593 = 1,645
Lopuksi
Määritettäessä lampun kuvun säde suhteelliseksi arvoksi 1.
Pallomaisen kappaleen pinta-ala A = 4 Pii r2
r1 => A = 4 pii 12 = 12,56 pinta-alayksikköä
r2 => A = 4 pii 22 = 50,24 pinta-alayksikköä
r4 => A = 4 pii 42 = 200,96 pinta-alayksikköä
Kaavassa, säteen kasvaessa kaksinkertaiseksi, pinta-ala kasvaa nelinkertaiseksi. Ajateltaessa lämmön jakaantuvan tasaisesti pinta-alalle. Säteen (r) mitan kasvaessa kaksinkertaiseksi, pienenee lämpömäärä pinta-alaa kohden 1/4 osaan. Lopulta köyden tai lampun arvojen muodostus ei poikkea toisistaan. Sama koskee muutakin, niin kauan, kun kaikki on johdettavissa kaavaan E = m c c.
Huom! Aurinkovakion suuruus maan ilmakehän rajalla on 1,37 kW/m2 (709)
19. Nostokorvat teräsrakenteisiin
Nämä nostokorvat eivät ole vinoon nostoon. Terävät nurkat poistettu
Nostokorvakkeiden muuttujina ovat levynvahvuus ja jännitys suhteessa kuormaan.
Materiaali S235JRG2
Nostokyky Levy Leveys Korkeus D Paino
kg mm mm mm mm kg Laskenta
1 500 8 100 90 58 0,30 Known weight
3 000 12 100 90 58 0,52 1,253 x 0,30 = 0,58 kg
5 000 20 100 90 58 0,87 1,255 x 0,30 = 0,91 kg
D = 40 mm pohjasta
1,6 - 2,0 - 2,5 - 3,15 - 4,0 - 5,0
1. 2. 3. 4. 5 (porras on potenssi)
Entä 6 300 kg nostokorvan paino?
1,6 - 2,0 - 2,5 - 3,15 - 4,0 - 5,0 - 6,3
1. 2. 3. 4. 5. 6.
1,256 x 0,30 = 1,14 kg
0,3 - 0,4 - 0,5 - 0,63 - 0,8 - 1,0 - 1,12 kg
1,5 2,0 2,5 3,15 4,0 5,0 6,3 x 1000 kg
1. 2. 3. 4. 5. 6.
Kuudes porras ylittää suhteellisuuden ja on usein yliviivattava. Tässä tapauksessa 1,12 kg on varsin tarkka paino 6,3 t korvakkeelle. Kuitenkin valitse materiaali S355, sillä materiaalin hinnan ero on pieni. (55)
20. Nostokorvakkeet 500 - 40 000 kg
Vasemmanpuoleisin nostokorvake on pienin kooltaan. Yhden nostokorvakkeen tiedolla, voi määrittää muiden nostokorvakkeiden painot. Esimerkiksi 40 000 kg nostokorvakkeen paino poikkeaa 5 kg valmistetusta nostokorvakkeen painosta. Painoero pienimmän ja suurimman välillä on noin 200-kertainen. Laskelman tekeminen vie hetken aikaa ja taulukkolaskentaan sijoitettuna ainoastaan muutaman sekunnin.
125 kg x 1,25 x 1,12 = 175 kg on viimeinen rivi laskennassa 40 000 kg nostokorvakkeelle.
Painon muodostumisesta tuotteessa, tulee ymmärtää suhteellisuus eri ulotteisuuksissa. Laskenta esittää myöhemmin kuvan nostokorvakkeiden painon määrittämisen. Paraabeli käyrän muodostumisesta on myös näkemisen geometriaa. (80)
21. Siltanosturi 2 t, 14 m
Piirustuksen siltanosturi on 30 vuotta sitten suunniteltu pienintä tuotesarjan kokoa vastaava tuote. Pieni tuote määrittää suurimman, mutta tarvittaessa myös toisinpäin. Vertaamalla tätä tuotetta, voi määrittää muut nosturit laskemalla.
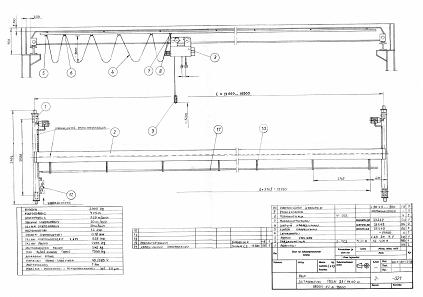
Laskenta esittää, kuinka poikkeavan rakenteen voi määrittää laskemalla. Vertailtavia ovat suurien nosturivalmistajien valmisteet. Pieni yksikannattiminen siltanosturi määrittää suuren kaksikannattimisen nosturin ja palataan takaisin kuvan nosturiin. Laskemme kaikki samaa tarkoittaviksi, joka tarkoittaa tuotteille yhteisiä toimintofunktioita. Nostaa ja siirtää, kuten siltanosturit mielletään toimiviksi. Helpoksi laskennan tekee se, että nostureiden suunnittelu perustuu standardeihin. Standardit määrittävät sallitun jännitystason jne. Standardien tavoin tämän määrittää suhteellisuus tuotteiden yhteydessä. (230)
28.1.2015*10:17
www.karikolehmainen.com
epcalculation@gmail.com |