Kone-elimien perusteita
1. Laakerin mitoittamisen periaate.
2. Laakerin laskennallinen käyttöikä.
3. Ruuvin tuotesarjan muodostuminen.
4. Ruuvivoimat ja kiristysmomentti
5. Ruuvin kannan mitat
6. Avainvälit ruuveissa
7. Metriset vakiomutterit
8. Teräsköyden tuotesarjan muodostuminen
8.1 Hehkulamppu
8.2 Teräs
8.3 Teräsköysi
1. Laakerin mitoittamisen periaate
Laakerin mitoittaminen laskemalla on jokseenkin yksinkertainen tehtävä. Laakereiden mitoitukset ovat usein perustapauksia, jolloin verrataan laakerin kuormitusta taulukon C arvoon. Laakeriin vaikuttaa normaalisti akselin- ja säteen suuntaisia voimia, jotka sisältyvät suhdelaskennan antamaan tulokseen.
Laakerin mitoittaminen päättelytehtävänä
 Suhdelaskennan esimerkeissä laakerin laskenta verrataan laskentaohjelmilla suoritettuun. Tulosten ero suhdelaskentaan nähden on pieni, mutta laskentanopeus on suuri suhdelaskennan eduksi. Ymmärtämällä suhteellisuuden, laakereissa, tuotesarjan laakerien valinta johdonmukaistuu ja tarjoaa tasaisen luotettavuuden. Laakereiden mitoitus liittyy vakioitaviin teräksiin, joilla molemmilla on lujuudellinen perusta.
Yritykset harvoin vakioivat komponenttien valintaa. Yrityksen jatkuva vaatimus on kuitenkin varastonimikkeiden ja varastoarvon pienentäminen. Varaston arvon pienentäminen jätetään usein kaupalliselle päättäjälle, jonka tekemillä päätöksillä ei useinkaan ole yhteyttä laakerien mitoitusarvoihin.
Laakerin arvot ulkoisista mitoista
Suhdelaskenta esittää harmonisen laakereiden mittasarjan niiden ulkoisten mittojen perusteella? => laakerin dynaamiset arvot määrittyvät laakerin ulkoisista mitoista => dynaaminen laakerin arvo määrittää laakerin eliniän => käsin kosketeltavien laakerin mittojen kautta määrittyy, käsin koskematon laakerin elinikä. Käytännössä laakerin elinikä testataan käytännön laboratoriokokeina, joista saadut arvot, suhdelaskenta pystyy osoittamaan suurella tarkkuudella. (113)
2. Laakerin laskennallinen käyttöikä
 Taulukko esittää laskennallisen käyttöiän, joka laitteilta yleisesti vaaditaan. Suhdelaskenta laskee laakereiden käyttöikiä ja yhdistää tiedon laitteiden toiminnalliseen ikään.
Tämä sillä, laiterakenteet mitoitetaan jännityksen tasoon, jossa väsyminen ei ilmene laitteen käyttöiän aikaisella kuormituslukumäärällä. Käytännössä jännitystaso on suuruudeltaan sellainen, jolla väsyminen ei ilmene kuormituksen lukumäärällä eli laite kuluu väsymättä.
Laakereiden kestoikä tunneissa
Kotitalouskoneet yleisesti 500 - 2 000
Laitteet joita käytetään satunnaisesti 2 000 - 4 000
- henkilöautot
Hissit 8 000 - 12 000
Kuljettimet ja pienet sähkömoottorit 12 000 - 20 000
Useat rata-ajoneuvot 20 000 - 40 000
Suuret sähkömoottorit ja pumput
Voimalaitosgeneraattorit
Laivapotkureiden laakeroinnit 80 000 - 200 000
Kestoikä kilometreinä
Pyörän laakeroinnit tieajoneuvoissa
- Henkilöajoneuvot (100 000) 200 000
Tällä hetkellä monet automallit eivät suoriudu vaadittavasta kestoiästä kilometreinä. Tämä johtuu laakereista puuttuvasta suojauksesta vettä ja likaa vastaan.
- Rekka-autot ja linja-autot 300 000 ...
Junavaunut lyhyillä matkoilla 800 000 - 1 500 000
Junavaunut pitkillä matkoilla 3 000 000
Veturit lyhyillä matkoilla 3 000 000 - 4 000 000
Sähkö- ja dieselveturit pitkät matkat 3 000 000 - 5 000 000
Laakereiden kestoiän tunneissa tai kilometreissä voi määrittää suhteellisena. Tämä siksi, että vertailu laitteiden välillä helpottuu. Tunnin (60 minuutin) ja 100 km välinen suhdeluku on 1,618 eli kultainen leikkaus (1,9 % tarkkuus). Taulukko yllä, kuten sen laakerivalmistajat keskimäärin esittävät. (358)
3. Ruuvituotesarjan muodostuminen
Metrisiset ruuvit
Tarkastellaan, kuinka ruuvituotteet noudattavat kultaista leikkausta kertoimena 1,618 ja suhdelukujonoa kertoimena 1,25. Aluksi tunnetaan ruuvit M4 ja M5. Tästä voi päätellä, ruuvin koon kasvavan suhteessa 5/4 = kertoimella 1,25. Käytännössäkin M20 on suurin ruuvi, jolloin tätä suuremmat ruuvit poikkeavat hieman mitoitukseltaan, sillä olematta suurta merkitystä.
1,25 x 1,25 x 1,03 = 1,618 = kultaisen leikkauksen suhde
4 - 5 - 6(,3) - 8 - 10 - 12(,5) - 16 - 20 - 25
1,25 x 4 = 5 mm
1,25 x 5 = 6 mm
1,25 x 6,3 = 8 mm
1,25 x 8 = 10 mm
1,25 x 10 = 12 mm
1,25 x 12,5 = 16 mm
1,25 x 16 = 20 mm
Kultainen leikkaus 1,618
4 mm ruuvi: 4 x 4 = 16
5 mm ruuvi: 5 x 5 = 25 => 25 / 16 = 1,6(18)
8 mm ruuvi: 8 x 8 = 64
10 mm ruuvi/screw: 10 x 10 = 100 => 100/64 = 1,57 x 1,03 = 1,6(18)
16 mm ruuvi: 16 x 16 = 256
20 mm ruuvi: 20 x 20 = 400 => 400 / 256 = 1,57 x 1,03 = 1,6(18)
Seuraavat laskennalliset ruuvikoot ovat M25, M32 ja M40. Käytännössä vastaavat ruuvikoot ovat M24, M33 ja M42. Näistä M33 ruuvia ei suosita, vaikka ruuveja onkin edelleen saatavissa. Myöskään M40 ruuvikokoa ei ole, vaan se on M42. Tähän on syynsä, jota määritetä tässä.
Laadun ominaisuuksia ovat tuotteen käytettävyys ja turvallisuus. Havaitsemme ruuvien kokojen noudattavan kultaisen leikkauksen suhdelukua, joka takaa turvallisuuden. Laskettaessa jännitykset, havaitaan niiden olevan samalla tasolla kaikkien ruuvikokojen osalta.
0,785 x1,25 x 1,03 = 1
0,785 neliön ja ympyrän poikkileikkauksen pinta-alojen suhde
0,785 on teräksen ominaispaino
Laskimme ruuvien koon muodostumisen & lujuuden mudostumisen tuotteessa. Kuten kaikki ilmiöt ovat johdettavissa yksinkertaisesta kaavasta E = m c c, tuotteet määrittyvät yksinkertaisen tuotteesta, kuten ruuvi. Tarvitsee kuitenkin hahmottaa monta asiaa ennen tätä. Kirjoitan tästä sivuilllani. (707)
4. Ruuvivoimat ja kiristysmomentti
Metrinen vakiokierre
640 N/mm2 = Materiaalin 0,2 -raja
0,15 µ = Kierteen kitkakerroin
0,15 µ = Mutterin kitkakerroin
60ŗ = Kierteen kylkikulma
Suurin sallittu Mises jännitys on 640 N/mm2 / 1,1(1) = 576 N/mm2
0,4 - 0,5 - 0,63 - 0,8 - 1 - 1,25 - 1,6 - 2,0
M4 - M5 - M6 - M8 - M10 - M12 - M16 - M20
Seuraavassa taulukossa on annettuna tietona ruuvien vetojännitys, kiristysvoima ja kiristys-momentti. Saman voi laskea yksinkertaisella tavalla, joka osoitetaan taulukossa. Tässä laskenta (suluissa) perustuu pienimpään tunnettuun M4 ruuviin.
Vetojännitys Kiristysvoima Kiristys-
maks. maks. momentti
N /mm2 N Laskenta Nm Laskenta
M4 559,36 4911 - 2,6 -
M5* 562,61 7989 (1,618 x 4911= 7946) 5,0 (21 x 2,6 = 5,2)
M6** 561,22 11280 (1,6182 x 4911= 12857) 8,6 (22 x 2,6 = 10,4)
M8 563,34 20618 1,6183 x 4911= 20802 20,7 23 x 2,6 = 20,8
M10 564,52 32742 1,6184 x 4911= 33658 40,2 24 x 2,6 = 41,6
M12*** 565,26 47652 1,6185 x 4911= 54458 68,3 25 x 2,6 = 83,2
M16 568,52 89257 1,6186 x 4911= 88113 165,0 26 x 2,6 = 166,4
M20 568,52 139286 1,6187 x 4911= 142567 322,5 27 x 2,6 = 332,8
M24 568,52 200686 1,6188 x 4911= 230674 554,6 28 x 2,6 = 665,6
* Fibonaccin lukujono alkaa 1 - 1 - 2..., samoin Pascalin kolmio. Pienintä tunnettua seuraava on 1 + 1 = 2
2,6 x 2 = 5,0 (ei desimaalitarkkuudella)
** Suhdelukujonon ruuvin koko on M6,3 (0,5 - 0.6,3 - 0,8), jota ei ole. Tämän voi yksinkertaistaen muuntaa laskelmassa M6 ruuviksi.
(6/6,3)4 x 12857 = 10577 (6/6,3)5 x10,4 = 8,2
*** Suhdelukujonon ruuvin koko on M12,5 (1 - 1,25 - 16), jota ei ole.
(12/12,5)4 x 54458 = 46254 (12/12,5)5 x 83,2 = 67,8
(24/25)4 x 230674 = 195922 (24/25)5 x 665,6 = 542,7
2 x pinta-ala = 4 2 x pinta-ala + momentti = 5
4.1 Esimerkki
M16 ruuvin kiristysvoima taulukon mukaan on 89257 N. M16 ruuvin haluttu kiristysvoima on 25 % pienempi eli kiristysvoima 89257 N /1,25 = 714056 N
=> Kiristysmomentti = 165 Nm /1,25 = 132 Nm
(390)
4.2 Esimerkki
M16 ruuvin kiristysmomentiksi halutaan 40 Nm. Mikä on ruuvin kiristysvoima? Laskelma pätee kevyesti voideltuihin ruuveihin, josta seuraa (40 Nm/165 Nm) /89267 N = 21640 N
Esimerkiksi ruuvin venyminen ei vaikuta. Sillä, jos venyy, ei kiristä. Kiristysvoima syntyy ruuvin kaltevaa tasoa vastaan kohdistuvasta voimasta ja näin on suhteellisesti laskettavaa. Lähes kaikki on vastaavasti laskettavaa, kun tunnistaa tapauksen mekanismin.
5. Ruuvin kannan mitat
Kun yksi mitoista tunnetaan, muut ovat tunnettuja.
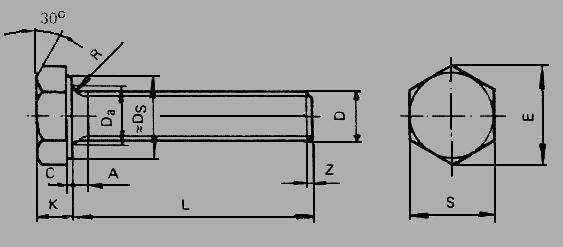
1 + 1,618 = 2,618
S E K Laskenta
M4 7,0 7,74 1,11 x 7,0 = 7,77 2,8 7,70 / 2.618 = 3,0
M5 8,0 8,87 1,11 x 8,0 = 8,86 3,5 8,87 / 2,618 = 4,0
M6 10 11,05 1,11 x 10 = 11,20 4,0 11,05 /2,618 = 4,2
M8 13 14,38 1,11 x 13 = 14,43 5.5 14,48 / 2,618 = 5,5
M10 17 18,90 1,11 x 17 = 18,87 7,0 18,90 / 2,618= 7,2
M12 19 21,10 1,11 x 19 = 21,09 8,0 21,10 / 2,618 = 8,1
M16 24 26,75 1,11 x 24 = 26,64 10,0 26,75 / 2,618 = 10,2
M20 30 33,53 1,11 x 30 = 33,30 13,0 33,53 / 2,618 = 12,8
M24 36 39,98 1,11 x 36 = 39,96 15,0 39,98 / 2,618 = 15,2
2 x 3,14 / 1,25 = 5
S E K Laskenta
M4 7,0 7,74 2,8 (7,0 + 7,74) / 5 = 3,0
M5 8,0 8,87 3,5 (8,0 + 8,87) /5 = 3,4
M6 10 11,05 4,0 (10 + 11,05) /5 = 4,2
M8 13 14,38 5.5 (13 + 14,48) /5 = 5,5
M10 17 18,90 7,0 (17 + 18,90) /5 = 7,2
M12 19 21,10 8,0 (19 + 2,618) /5 = 8,0
M16 24 26,75 10,0 (24 + 2,618) /5 = 10,2
M20 30 33,53 13,0 (30 + 33,53) /5 = 12,7
M24 36 39,98 15,0 (36 + 39,98) /5 = 15,2
(212)
6. Avainvälit ruuveissa
Ruuvin kannoista tiedetään 4 mm ruuvin avainväli 7 mm ja 5 mm ruuvin avainväli 8 mm.
7 mm / 4 mm = 1,75
8 mm / 5 mm = 1,60
Kultainen leikkaus
Määritämme avainvälin kultaisen leikkauksen suhteeseen 1,6(18) perustuen;
4 mm x 1,618 = 6,472 - 5 mm x 1,618 = 8,09
6,472 mm => 7,0 mm
8,09 => 8,0 mm
Metrinen ruuvisarja
4 - 5 - 6 - 8 - 10 - 12 - 16 - 20 Ruuvit mm
7 - 8 - 10 - 13 - 17 - 19 - 24 - 30 Avainväli mm
4 x 1,6(18) = 6,4 mm
5 x 1,6(18) = 8,0 mm
6 x 1,6(18) = 9,6 mm
8 x 1,6(18) = 12,8 mm
10 x 1,6(18) = 16 mm
12 x 1,6(18) = 19,2 mm
16 x 1,6(18) = 25,6 mm
20 x 1,6(18) = 32 mm
10 mm ruuvi; avainväli voisi olla 16 mm, 17 mm sijaan.
16 mm ruuvi; avainväli on pienempi, kuin määritetty 25,6 mm.
20 mm ruuvissa on laskemalla määritetty 32 mm, mutta valittu kooksi 30 mm.
Kaikki määritetyt avainvälit täyttävät ruuvin vaatimukset.
(708)
7. Metriset vakiomutterit
0,8 - 1,0 - 1,1(2) - 125
Mutterin mitat voi laskea suhdelaskentana.
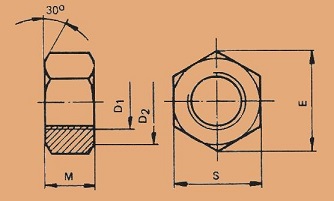
Mutteri
S E M
M3 5,5 6,08 1,11 x 5,5 = 6,11 2,4 0,8 x 3,0 = 2,4
M4 7,0 7,74 1,11 x 7,0 = 7,77 3,2 0,8 x 4,0 = 3,2
M5 8,0 8,87 1,11 x 8,0 = 8,86 4,0 0,8 x 5,0 = 4,0
M6 10 11,05 1,11 x 10 = 11,20 5,0 0,8 x 6,0 = 4,8
M8 13 14,38 1,11 x 13 = 14,43 6.5 0,8 x 8,0 = 6,4
M10 17 18,90 1,11 x 17 = 18,87 8,0 0,8 x 10 = 8,0
M12 19 21,10 1,11 x 19 = 21,09 10,0 0,8 x 12 = 9,6
M16 24 26,75 1,11 x 24 = 26,64 13,0 0,8 x 16 = 12,8
M20 30 33,53 1,11 x 30 = 33,30 16,0 0,8 x 20 = 16,0
M24 36 39,98 1,11 x 36 = 39,96 19,0 0,8 x 24 = 19,2
174,56 174,36
Ajatus laskennassa on siinä, kuinka lähes minkä tahansa voi laskea suhteellisuuden kautta, kun tietää menettelyn laskennan suorittamiseksi. Tästä syystä tulee tuntea fysiikka, lujuuslaskenta ja pitää mieli avoimena. Entä ruuvin M39 mitat, jos tunnemme ruuvin M3 mitat? (184)
S E M
M3 5,5 6,08 1,11 x 5,5 = 6,11 2,4 0,8 x 3,0 = 2,4
M39 60 69,3 31 0,8 x 39 = 31,2
1,2511x 55 = 64
1,2511 x 6,08 = 70,8
1,2511 x 2,4 = 27,9
Porrastukset
... M24 - M30 - M39
9. 10. 11.
8. Teräsköyden tuotesarjan muodostuminen
Tällä kertaa tarkastelemme teräsköyttä 6x26 Warrington-seale ja havaitsemme, ettei käyttäytyminen ilmiönä poikkea hehkulampusta.
Teräsköysi - Hehkulampun valo
Käsin kosketeltava - Käsin koskettelematon
____________________________________________________
Ulotteisuudet
Pituus - Pinta-ala - Tilavuus - Aika
Valon nopeus on pinta-ala c2
____________________________________________
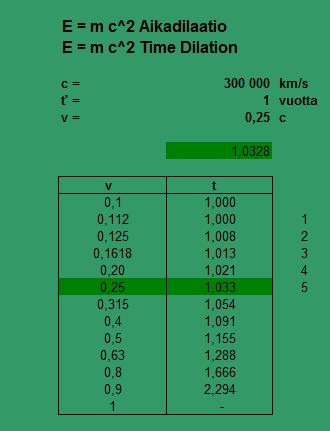
Miksi valitsin teräsköyden, johtuu siitä, että lopetin edellisen kirjoituksen näkemisen geometrian kuvioihin. Neliön ja ympyrän pinta-alojen suhde on aikadilaation määrittämä, jolloin yksikköympyrän pinta-ala on teräksen ominaispaino. Laskenta kuvioiden kautta ei olisi mahdollista, ilman tätä yhteyttä.
1 / (1.25 x 1.03) = 0.78
8.1 Hehkulamppu
Saamme energian auringosta. Aurinkoa emme voi tarkastella, joten on luotava pienimuotoinen avaruus. Tähän tarkoitukseen otamme hehkulampun kuvassa. Valo lampussa syntyy, kun hehkulanka kuumennetaan korkeaan lämpötilaan sähkövirran avulla, kunnes lanka hehkuu. Hehkulampuilla on valon tuottamisessa huono hyötysuhde, noin 3 ... 5%, jolloin valo on lämmittämisprosessissa syntyvä kitka.
100 / 1,0328 = 96,82 %
Staattisen väsymisen kitka 1,033
8.2 Teräs
Wikipedia
Teräs on yleisnimi kaikille rautavaltaisille metalliseoksille, joita voidaan muokata valssaamalla tai takomalla. Teräksen hiilipitoisuus on 0,03–1,7 %. Tätä alhaisemman hiilipitoisuuden rautaseosta kutsutaan meltoraudaksi ja korkeamman valuraudaksi. Teräksen ominaisuudet riippuvat voimakkaasti sen rakenteesta, joka puolestaan riippuu hiilen määrästä, seosaineista sekä valmistusparametreista.
8.3 Teräsköysi
Teräsköysi on kannattamiseen tarkoitettu. Tarkastelussa havaitsemme köyden tuotesarjan muodostuvan vastaavalla tavalla kuin edellisissä esimerkeissä. Teräsköyden arvot, ovat tarkistettavaa taulukoista.
Halkaisija Paino
D mm kg/100 m
10 38,0
12 54,7 54,7/38,0 = 1,779
16 97,3 97,3/54,7 = 1,772
20 152,0 152/97,3 = 1,562
24 219,0 219/152 = 1,441
32 389,0 389/219 = 1,777
40 608,0 608/389 = 1,562
Keskiarvo = 1,649
1.618 x 1.0165 = 1,645
1 + (0.033/2) = 1.0165
10 - 12,5 - 16 - 20 - 25 - 32 - 40
Maailmankaikkeuden kaksiulotteisuuden sääntö määrittää kaksi kertaa kauempana olevan neljä kertaa suuremman. Arvoasema 10 => 16 on kaksi kertaa suurempi.
4 x 38 kg/100 m = 152 kg/100 m
16 x 38 kg/100 m = 608 kg/100 m
6x26 Warrington-seale (langan murtolujuus 15,7 kN/cm2 )
Taulukoitu tieto
D mm kN/cm2
10 55,9
12 80,6 8,06/5,59 = 1,442
16 143,0 143/80,6 = 1,774
20 224,0 224/143 = 1,567
24 322,0 322/224 = 1,438
32 573,0 573/322 = 1,780
40 895,0 895/573 = 1,562
Yhteensä = 1,593
1.618 / 1.0165 = 1,591
1 + (0.033/2) =1.0165
Vähimmäismurtokuorma on kuormitus, joka on saavutettava tai ylitettävä vetomurto-kokeessa.
4 x 55,9 = 223,6 kN/cm2
16 x 55,9 kN/cm2 = 894,4 kN/cm2
(1,649 + 1,593) /2 = 1,62 = kultainen leikkaus 1,618
1.033 x 1,593 = 1,645
Lopuksi
Määritettäessä lampun kuvun säde suhteelliseksi arvoksi 1.
Pallomaisen kappaleen pinta-ala A = 4 Pii r2
r1 => A = 4 pii 12 = 12,56 pinta-alayksikköä
r2 => A = 4 pii 22 = 50,24 pinta-alayksikköä
r4 => A = 4 pii 42 = 200,96 pinta-alayksikköä
Kaavassa, säteen kasvaessa kaksinkertaiseksi, pinta-ala kasvaa nelinkertaiseksi. Ajateltaessa lämmön jakaantuvan tasaisesti pinta-alalle. Säteen (r) mitan kasvaessa kaksinkertaiseksi, pienenee lämpömäärä pinta-alaa kohden 1/4 osaan. Lopulta köyden tai lampun arvojen muodostus ei poikkea toisistaan. Sama koskee muutakin, niin kauan, kun kaikki on johdettavissa kaavaan E = m c c.
Huom! Aurinkovakion suuruus maan ilmakehän rajalla on 1,37 kW/m2
21.6.2018*08:00 (845 - 265)
www.karikolehmainen.com
epcalculation@gmail.com |
