Strength of Materials
1. Introduction to Strength of Materials
2. Pseudoscience and Strength of Materials
3. Letter Codes for Strength of Materials
4. Greek Alphabet to Calculation
5. Iron After Big Bang.
6. Steel Pentagon
7. Steel
7.1 Steel to Mechanical Engineering
8. Steel Strength as Visual Geometry.
9. Strength, Such as Visual Geometry.
10. Standard Steels Comparison
11. Permissible Stresses
12. Steel Hardness Determining
13. Load types - Normal Force
14. Young's Modulus.
15. An other Way Calculate the Srength of Materials
16. Load and Force 1 kN.
17. Standard Numbers.
18. Product Value Space.
19. Gravitational Force.
20. Hookes's Law.
.....................
22. Free Fall of a Body
- Round bar 10 mm static values
23. Circle and Square Areas
24. Specific Gravity of steel
24.1 Circle and Ellipse
24.2 Steel Unit Circle and Aluminium
25. Forces in a Matter
.............................
30. Magnitude of Gravity on the Earth
31. Shadow of the Bending
32. Shadow Behind the Pascal's Triangle.
33. Fourth Dimensionality of Bending.
34. Bending Generally
35. Static Values to Cross-Sections
36. HEB I-Profiles Static Values
37. HEB Cross-Section Areas.
38. HEB I-Profiles 1 kN Load Bearing.
39. Static Values of the Wall Thickness.
40. Allowable Stresses, Steel
40.1 Magnitude of Stresses
40.2 Fatigue Loading
41. Impact Strength of Steel.
42. Steel Hardness and the Breaking Strength
42.1 Steel Hardness, the Golden Ratio
...........................
51. Axial Deformation
52. Axial Deformation of a Beam
53. Missing Moment of the Wire.
54. Weight of a Steel Plate
54.1 Thickness of the Plates
55. Round Bars Stock Item Set
56. General of Measuring
57. Normal Stress Calculation
- compression and pulling force
58. Bending Case 1 Calculation.
- bending force in the middle of the girder
59. Pascal's Triangle Factor 11
60 Golden Triangle
61. Axial Deformation.
62. Space Diagonal in the Strength Calculation
70. Calculation Examples
1. INTRODUCTION TO STRENGTH OF MATERIALS
Many books have written of the strength calculation. For this reason, it is not necessary to repeat the written words, but to look at things from a perspective that has not overlooked. It is good to have the control over the strength to some extent. Thus, there is no tendency for the basics. The written is to a great extent the same, because after all, things have the same meaning. We are finishing there we started. Of the written is good to remember the number five (number of fingers) and the review of iron, which is called steel.
When designing products, it is good to understand the universal conformity to law that in every material affects. Let us consider the formula given result in the form of graphics. When formulas the result of the calculation is non-linear and it cannot get the result of the calculating formula by the deduction. Or you may, if you can proportionality, but it does not exist to manage.
f = 5 x F x L3 / ( 384 x E x I )
Many books have written of the strength of materials. For this reason it is not necessary to repeat the written words, but to look at things from a perspective that has not overlooked. To the reader it is good to have the control over the strength of materials to some extent, but it is not necessary. Everything has ultimately the same meaning and origin, so it happens repeating in the things. After all, the beginning of everything is based on the formula
E = m c c
having the same begun. In context to written, it is good to remember the number of five fingers. Also not forgetting the review association to iron, called steel. It should be noted that there are few people who actually know how to form the proportionality in their minds. You can test it right away, first by calculating the following two simple tasks.
1.03 x 1.03 = ? a) 1.09 b) 1.0009 c)1.0009 d) 1.06 (1.03 + 1.03 = 1.06 ?)
1.06 x 1.06 = ? a) 1.36 b) 1.036 c)1.0036 d) 1.12 (1.06 + 1.06 = 1.12 ?)
Previous tasks were difficult, so the perception of larger entities does not seem easier? Still, this means only a change to the approach in which the accustomed thinking does not take you very far. By simplifying the other hand, it is possible to perceive the things that would otherwise remain remain undetected. When designing the products, they include in the universal laws in the materials.
Let us think the calculation output in graphical form and the formula of bending. The outputs of of the calculations give the curve line of the deflection. Below is an example of a formula for the girder deflection to determines the deflection of its own weight.
f = 5 × F × L 3 / (384 x E x I)
Having one calculated point of the deflection, the other deflections (sags) are known with the help of EP-calculation. The formula below derives from the best-known energy formula. These two formulas with other formulas set up everything else through the same meaning and thus knowing a single value is known for a lot of other things, and some geometric patterns join to this. Finally there is no need to so many formulas.

Deflection line of a beam

Something known Something not
The scale (equilibrium level) in the picture describes the EP-calculation, which is based on levering the balance of the weights. When non-touchable scale, the weights are abstract values. Let us think one stone and one bag of sand. Put the stone onto one side of the balance and put sand onto other side of the scale. When the scale has the balance, it has its horizontal position. We do not need to know the weight of the stone to determine the same amount of sand in weight. If the stone weight is known, the amount of sand is not reasonable try to calculate. Many things are like sand which can determines by the way of proportionality.
It should be remembered that the basis of calculation or calculation outputs do not deviate from what is obtained by calculating the other way. To reaffirm this notion, the conventional strengh of materials basis will be added to this survey. (886)
2. PSEUDOSCIENCE AND STRENGTH OF MATERIALS
Pseudoscience is a claim, belief or practice which lacks scientific status mainly either because it is incorrectly presented as scientific but does not adhere to a valid scientific method, or because it cannot be reliably tested.
After of twenty years of mechanical engineering consultant, I could not help noticing things that were repeated in different contexts. As a result, the EP-calculation's Finnish name is "the same meaning ratio calculation". One of the first findings was; in this time the teaching is the best of what science can offer. Still, quite a few graduated from the University dominates the basics of engineering design. This is detected in simple machine component dimensioning, which have not been done. The exception are those who are able to calculate on behalf of the others.
Strength of Materials, also called mechanics of materials is an extension in physics area, investigating the behavior of solid particles of internal and external loads acting on matter.
3. LETTER CODES FOR STRENGTH OF MATERIALS
Symbol Description
α (alfa) Angles in general
a The side (a,b,c .), distance commonly
A The reaction in the strength calculations
B The reaction, whereby generally two reactions A and B
C Rigidity as the deflection/length ratio to the support length 1:1000, 1:200...,
Bearing's dynamic carrying capacity
C0 Bearing's static carrying capacity
d Diameter of the rivet or screw, thickness of the web plate
D Outer diameter of a body, the diameter of the rivet base and so on.
e The edge distance from the center of gravity axle, eccentricity
E The Young's modulus of elasticity (21000 kN/cm2)
φ (fii) The Golden Ratio 1.618
f Deflection, initial crookedness
F KN force (= 100 kg) => F10 corresponding to a load of 1000 kg
Fn The buckling force to strength measuring
Fv Pre-tightening force of a screw when installing
g Uniformly distributed dead load
The size effect number to strength measuring
Acceleration of free fall 9,82 m/s when a falling body
G Modulus of shear deformation (sliding factor) 8000 kN/cm2
Material weight in kg/m
h Uumalevyn korkeus
Height of the web plate
Profiled steel's nominal height
Generally height
I The second moment of area
Ix The second moment of area to x - x axis
Iy The second moment of area to y - y axis
µ (myy) Friction coefficient commonly
L Load length, lengthwise the girder or length generally
Ln Buckling length to strength measuring
M Moment of the power when measuring the structural element
Mt Bending moment when measuring the structural element
Mv Torque when measuring the structural element
n Safety factor, number of steps in ratio queu
N Normal force to strength measuring
p The surface pressure as the general concept in whole defining
π (pii) Factor 3.14159 as a circle's circumference to its diameter
P Concentrated load and power to strength and energy definitions
r Smaller radius, especially to fatiguing measurement
R Larger radius, especially to fatiguing measurement
s Material thickness to strength defining
σm (sigma) The yield limit in material to strength defining
σM The breaking strength in the material - The ultimate tensile strength
σn The nominal stress, buckling stress to strength defining
σt Bending stress to strength defining
σtsall Permitted bending stress when strength defining
σT Endurance limit for pulsating to strength defining
σv Resistance to torsion to strength defining
σW Endurance limit for reversed stress to strength defining
t Time commonly
τ (tau) The shearing stress commonly to strength defining
v Poisson's ratio (0,3 to steel) to strength defining
Wx Bending resistance to x - x axis
Wy Bending resistance to y - y axis
= ; # Equivalent ; no equivalent
=> This results in
4. GREEKS ALPHABET TO CALCULATION
Α α alpha
Β β beta
Γ γ gamma
Δ δ delta
Ε ε epsilon
Ζ ζ zeta
Η η eta
Θ θ theta
Κ κ kappa
Λ λ lambda
Μ μ myy
Ξ ξ xi
Π π pii
Ρ ρ rhoo
Σ σ sigma
Τ τ tau
Φ φ ffii
Ψ ψ psii
Ω ω omega
5. IRON AFTER BIG BANG
Strength needs to calculate the material iron, the most common element on Earth. Iron, named steel is the material for this purpose. EP-Calculation five steps is the proportionality limit in values and iron is on this step, the temperature of 4000 Kelvin. The heavier material than iron needs for formation the nuclear fusion. We stay in steel grades (S235 and S355), ie. to the temperature of 4,000 Kelvin, as the table shows. The lighter elements than steel make up 99.99997 % of the composition of stars. Heavier elements than iron are a small minority, but they are two-thirds of the elements.
The formation of metal
Nuclear reaction Temperature 106 K Pascal's triangle
0. Hydrogen => helium 10 - 40 1
1. Helium => carbon, oxygen 100 -200 1 1
2. Carbon => neon, sodium, magnesium 800 1 2 1
3. Neon => magnesium, silicon 1 700 1 3 3 1
4. Oxygen => silicon, sulphur 2 100 1 4 6 4 1
5. Silicon => titanium, Zinc, nickel, Iron 4 000 1 6 1 1 6 1
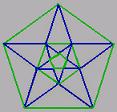 Pascal's triangle, the lowest row is the fifth row from the output value of 0. Row five finds the golden ratio 1.618, even the value of 1.611 is slightly different. Pascal's triangle, the lowest row is the fifth row from the output value of 0. Row five finds the golden ratio 1.618, even the value of 1.611 is slightly different.
The fifth element describes the pentagon where the golden ratio occurs in many. This is described in visual geometry and strength calculation. (985)
6. STEEL PENTAGON

Five material properties.
6.1 Hardness
Hardness is used to the ball bearing races etc. whereby bears lifelong load, also in die cutting tools is used hardened steel. Hard, hardened material stand pressing load and even impact loads as in die cutting tools.
6.2 Softness
For example Ultra-strength steel materials need local softness to shape them by bending and forming.
6.3 Toughness
Tough constructional steel material can bend, share, pull, press, and twist. Material does not break, such as a brittle material do after small elongation. To the tought material it is defined elongation curve, which obeys Hooke's law.
6.4 Brittleness
A brittle matter cannot stand pulling force, as an example of a concrete column. In buildings and columns, the steel stiffened concrete is an economical way to build large load acceptable structures. Concrete is not sufficien to the bending structure, this without elimination of tensile stress for example with the help of the prestressed wires.
6.5 Elasticity
The elastic structure of hard steel is made with the help of spring steel and dimensioning the structure flexile. In the helical spring, small cross-sectional profile is twisted to take torsion. Tension in the spring can be determined with the help of the simple calculation. (345)
7. STEEL
To calculate strength, there is need for a iron, later named to steel. EPC calculation born in the same as the gravity started, having the proportional limit five steps between values. From the table can see that iron has placed itself onto the fifth step (phase, stage) having the birth temperature 4.000 Kelvin.
Heavier than iron require energy for the production of heavier nuclei => nuclear reaction. We stay to iron (steel S235 and S355) and under 106 Kelvin as the table shows..
Elements lighter than iron form 99.99997% of stars ordinary matter.
Elements heavier than iron are a small minority, but the number is two-thirds of the elements.
"Steel is an alloy of iron and a small amount of carbon. Carbon is the primary alloying element, and its content in the steel is between 0.002% and 2.1% by weight. The material is significantly hardened and strengthened by impurities, such as carbon, from the smelting process. A certain proportion of carbon (between 0.002% and 2.1%) produces steel, which may be up to 1000 times harder than pure iron. Iron metal has been used since ancient times, though copper alloys, which have lower melting temperatures, were used first in history. Additional elements may also present in steel: manganese, phosphorus, sulfur, silicon, and traces of oxygen, nitrogen and aluminium". Wikipedia
Text from history continues;
Ancient Greece was a Greek civilization belonging to a period of Greek history that lasted from the Archaic period of the 8th to 6th centuries BC to the end of antiquity (ca. 600 AD).
Now we have located iron to history, or have we? There is also older meteoric iron, but the found material was mostly used to jewelries not tools.
"Meteoric iron is a native metal found in meteorites and made from the elements iron and nickel mainly in the form of the mineral phases kamacite and taenite. Kamacite and Taenite are the principal iron-nickel alloy minerals in iron meteorite. Meteoric iron makes up the bulk of iron meteorites but is also found in other meteorites. Apart from minor amounts of telluric iron, meteoric iron is the only naturally occurring native metal of the element iron on the Earth's surface."
Iron Plate in the Great Pyramid

Samples of smelted iron from Asmar, Mesopotamia and Tall Chagar Bazaar in northern Syria were made sometime between 2700 and 3000 BC
7.1 STEEL TO MECHANICAL ENGINEERING
Steel used to mechanical engineering is well-defined. When using steel to demanding construction, there is available the material certificate. The certificate can be submitted to the authority, as well as to the end customer. As a result of steel homogeneity and documentation, the reliable calculations are possible. The calculations can be used to an another plan, material is uniform, and it can be found all over the universe.
For example when wood, it is not like steel. The quality of the material varies in the different parts of the world. Plastics meet the uniformity requirement in many respects, if they had a standard uniform composition. The use of plastics products is limited, and therefore does not fit for the review. Wood decays easily, is flammable, has low resilience to wear and tear, swells when it gets wet and shrinks when it dries.
Structural analysis is, however, advanced in metallurgical products. Production methods of steel have also more industry activities, than the wood has. The calculation reveals the relationship between the steel and the natural phenomena related to proportionality, which opens entities. Non-alloy steel shows the proportionality properties of the steel. (888)
8. STEEL STRENGTH AS VISUAL GEOMETRY
Plato's Cave Example
Allegory of the Cave
According to Plato, the picture of the reality had born of real objects which formed shadows onto the cave's back wall. In Plato's example, the prisoners came for the first time freedom, but had to return back to the cave. Before only shados seen prisoner told of the real objects behind the shadows, but the other prisoners did not want to believe. As a result, other prisoners rather wanted to kill the prisoner, than to change their own idea of the reality. These others may not differ from us, if the not casted shadows are not familiar to us. Knowledge gives the opportunity to see the kind, which, without the knowledge is not possible. Let me to explain the idea a little more.
1 - 1.12 - 1.25
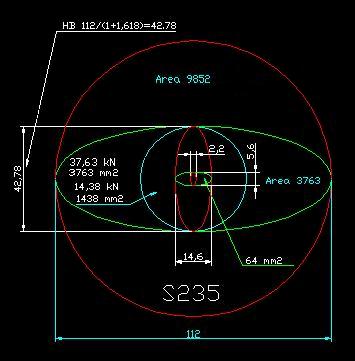
That what we have a lot of, it is the world's iron subsoil. Normal structural steel S235 hardness for the strength calculation is HB 112, the average value from HB 100 to 125. The round shape of a diameter 112 (*units are yours), includes the diameter of the scale, the hardness of the steel S235. Anyone can do the circle having diameter of 112 units, when the two-dimensional circle represents the hardness onto the paper. The circle forms the area of 9852 square units, gravity 9,82 units/s2 in other words . By making a three-dimensional ball of the circle, it can determine the hardness of the steel. Pressing the ball onto the surface of the steel, is the used method to determine hardness. Below is a pattern, of which can continue to determine the strength. Not onto the wall casting shadow, of the invisible phenomenon called strength. In the same way as the visible is seen as a shadow, invisible has the calculable not seen shadow. In addition to the calculation, the Invisible has also a geometric counterpart. You think that I am talking about the issue, which I can not know. I can hand on my heart say the calculation has progressed long way, but completely ready it will never be.
* Units are human fabrications, such as mm, inch, light year, etc. (906)
Hard objects such as a chair can form a shadow on the wall. Soft value can shape a pattern on the paper, but not cast a shadow on the wall. (859)
9. STRENGTH, SUCH AS VISUAL GEOMETRY
 The calculation includes an explanation to the mathematical ratio of 1.618. This is presented in steel and different kind of structures having strength perspective. Data is common for architects, engineers and professional people in all areas. The calculation does not limit anyone. The calculation includes an explanation to the mathematical ratio of 1.618. This is presented in steel and different kind of structures having strength perspective. Data is common for architects, engineers and professional people in all areas. The calculation does not limit anyone.
Product Designer is not an actual designer, but using the number ratio of 1.618 and its squared ratio of 1.25 is a great opportunity to design a pleasant-looking objects. We find the strength of the structure to comply with the ratio of 1.618.
In the examples we go through the calculation of the strength of bending to fatigue.
We find the strength to move relative to products. By calculating correct one product, the other a series of products are with high probability proportionate. The Equivalent Proportional Calculation is a mathematical construct that has no end.
These studies, we do not just in products, we make it to all possible phenomena. Constraint is our experience in managing a normal solution. Previous, because we need the experience to compare the traditional calculation and The Equivalent Proportional Calculation. (299)
10. STANDARD STEELS COMPARISON
_____________________________________________________________________________ __
Yield Breaking Impact EN 10025-2 EN SFS 200 DIN 17100 BS 4360
strength strength strength 2004 10025:1990 1986 1980 1986
ơm ơM KV J t °C +A1:1993
235 360 -510 27 20 – S235JR - St 37-2 -
235 360-510 27 20 S235JR S235JRG2 Fe 37 B RSt 37-2 40 B
235 360-510 27 0 S235J0 S235J0 St 37-3 U 40 B
235 360-510 27 -20 S235J2+N S235J2G3 Fe 37 D St 37-3 N 40 D
235 360-510 27 -20 S235J2 S235J2G4 – – -
275 430-580 27 20 S275JR S275JR Fe 44 B St 44-2 43 B
275 430-580 27 0 S275J0 S275J0 – St 44-3 U 43 C
275 430-580 27 -20 S275J2+N S275J2G3 Fe 44 D St 44-3 N 43 D
275 430-580 27 -20 S275J2 - Fe 430 D2 – -
355 510-680 27 20 S355JR S355JR – – 50 B
355 510-680 27 0 S355J0 S355J0 Fe 52 C St 52-3 U 50 C
355 510-680 27 -20 S355J2+N S355J2G3 Fe 52 D St 52-3 N 50 D
355 510-680 27 -20 S355J2 S355J2G4 – – -
355 510-680 40 -20 S355K2+N S355K2G3 – – 50 DD
355 510-680 40 -20 S355K2 S355K2G4 – – -
185 310-540 – – S185 S185 Fe 33 St 33 A 33 -
295 490-660 – – E295 E295 Fe 50 St 50-2 -
11. PERMISSIBLE STRESSES
Everywhere in the Universe being iron has carbon. Carbon remowal of the iron, makes the iron steel. Steel can weld and manufacture different kind of structures and machine parts. Steel is well known and it can determine in advance the permissible stress values to load cases. The table below has the base to universal strength dimensioning. Steel proportionality does not differ from other phenomena.
Tabled Values kN
Material thickness ...16 mm
Steel S235 E295 S355 E355
Lower yield limit 22.0 28.0 34.0 32.0 1.56 x S235 = S355
Proportionality: 1 - 1.25 - 1.6 1.252 = 1.56 1.252 x 1.03 = 1.618
Tensile, Compression and Bending
Normal load case 14.7 17.0 22.7 20,0
Rare load case 16.9 19.0 26.1 22.0
Share
Normal load case 8.8 10.0 13.6 12.0
Rare load case 10.1 11.5 15.7 14.0
Edge Pressure
Normal load case 26.9 - 38.0 - 1.40 x S235 = S355
Rare load case 30.0 - 43.0 -
Hertz case
Normal load case 65.0 80.0 95.0 90.0 1.46 x S235 = S355
Rare load case 75.0 90-0 105.0 100.0 1.40 x S235 = S355
Material Thickness 17...40 mm
Steel S235 E295 S355 E355
Lower yield limit 21.0 27.0 33.0 31.0 1.56 x S235 = S355
Tensile, Compression and Bending
Normal load case 14.0 17.0 22.0 20.0
Rare load case 16.2 19.0 25.3 22.0
Share
Normal load case 8.5 10.0 13.2 12.0
Rare load case 9.7 11.5 15.2 14.0 1.43 x S235 = S355
Edge Pressure
Normal load case 26.9 - 38.0 - 1.41 x S235 = S355
Rare laod case 30.0 - 43.0 - 1.43 x S235 = S355
Hertz case
Normal load case 65.0 80.0 95.0 90.0 1.46 x S235 = S355
Rare load case 75.0 90.0 105.0 100.0 1.40 x S235 = S355
12. STEEL HARDNESS DETERMINING
EP-calculation gives a mathematical model to determine the hardness of steel by knowing about the hardness or tensile strength of the material. At the same time receiving the necessary Wöhler curve for fatigue dimensioning and the EP-calculation option. The wear of bearing, bending of the bar, time running race can not according to formula E = m cc differ from 4d-world. Iron (steel) as the strength is not an end in itself, but rather the introduction of the EP-calculation in order to understand more of its formation. In order to ensure the model begins by examining the concept of the hardness of the known data.
Measurement Methods
- HB General Method of measurement of less than 400 HB hardness
- HRV Hardened and surface hardened steels
- HRB Method Rarely used
- HV Nitrided steels
- Shore Rubber
To surface hardness and a variety of surfaces can not set a common method of measurement, or an absolute value between them. Measuring the magnitude of the surface hardness is used jointly agreed measurement methods and systems, which are listed above. Each of these measurements only provide a method tied to the benchmark, which have limited comparing between the different methods.
Brinell test use hard balls, the load marking for example HB 10/3000/30. The ball is D = 10 mm, the force F = 3000 kps (30 kN), t = 30 sec. Normal test HB 10/3009/10 is usually marked by HB. At higher hardness than HB 400 the ball flattens, causing the result inaccuracies. HB hardness can also measure by Poldi method, which is used for example, to comparison of test-pieces.
Of the Rockwell hardness tests, the most common is HRC ( Cone) and the HRB (ball) methods, but the method is rarely used.
HRC hardness test is used to measure the hard pieces, if the surface layer is thick enough to press the cone into it. If the cone goes through the hard layer, is the result an incorrect value.
Vickers hardness test, the compressive force varies from 0.5 to 120 kgs (0.05 to 1.2 kN ). HV hardness is measured in particular of thin surface layers.
The Poldi method has a comparative measurement with a known ( poldi ) material , setting a hardened test ball between the Poldi and test material. After hammer hitting a ball by comparing the pit area of the test material to Poldi material's pit. The test will thus correspond the Brinell test, but being less accurate .
Due to simplicity of the method it was used in previous wars to the destroyed enemy tanks. This to get to the targets a sufficient firepower. The writed seems plausible. (11231)
Breaking Vickers Brinell
Strength Hardness Hardness
ơM HV10 HBW
350 110 105 350 / (3.14 x 1.03282) = 104.5
360 112 107 S235 steel
370 115 109
385 120 114
400 125 119
430 135 128
450 140 133
465 145 138
480 150 143
495 155 147 E295 steel
510 160 152 S355 steel
530 165 156
545 170 162
560 175 166
575 180 171
595 185 176
610 190 181
625 195 185
640 200 190
660 205 195
675 210 199
690 215 204
705 220 209
720 225 214
740 230 219
755 235 223 755 / (3.14 x 1.03282) = 225
The EP-calculation means, the world may not need such a large number of tables and calculations, if it isknown the universal formation of phenomena. Hardness is based on the determination of the surface area, such as the speed of light is squared in the best-known energy formula and is the light coverage. Later a small pit in a material determines its features, but do not get ahead of ourselves .
The speed of light c 0.25 and time dilation of 1.0328 for the mass and time is a good start.
1,252 x 1.03 = 1,618 Phi
1,252 x 2 = 3,14 Pi
3,14 x 2 = 6,28 2 Pi radians
If I'm not badly mistaken, nowhere has not previously been shown the mathematical formation of steel hardness on the basis of material strength. Let this be one certificate of the calculation reality. In a similar manner the other properties of the material have their proportionality according to relativity physics.
13. LOAD TYPES - NORMAL FORCE
Prepared designs are different from each other, but they can distinguish to five main types of loadings, enabling them to be dimensioned in a product. Some forces alone determine the dimensions, some are combinations of two different forces. The force F or the force combinations ( 6 - 7 ) load a rod-shaped body.
Normal Force
Si system, the normal force in newtons (N ) is a mechanical quantity. The concept of the normal force is needed to determine the strength of the materials, to find out the cross-sectional tension level. In connection with the normal friction force, it is the component, perpendicular to the surface (surface being a plane) of contact, of the contact force exerted on an object by, for example, the surface of a floor or wall, preventing the object to fall.
The following three load types generates the so-called nominal force
F <= ========== => F
1. Pulling, where the force resistance demands pulling strength of the material.
- normal force, perpendicular force against the reviewed surface
- the pulled body may be long, the cross-sectional stress level determines the force
- the force gets the nominal value of 1
F => ========== <= F
2. Compressing, where the force demands compressing strength of the material. - normal force, perpendicular force against the reviewed surface
- the rod is short enough, the tension level determines the amount of force
- the rod is long enough, buckling determines the amount of force
- the force gets the nominal value of 1
3. Bending, where the force demands bending strength of the material.
- normal force, perpendicular force against the reviewed surface
- the cross-sectional - pulling and compressing - stress level determines the force
- the force gets the nominal value of 1
Cutting forces
4 Cutting, where the force demands cutting strength of the material
- Cutting force, the transverse force against the reviewed surface
- the tension level determines the amount of force
- the force gets the nominal value of 1.61 ...
5 torsion, where the force demands torsionstrength of the material
- cutting force, the transverse force against the reviewed surface
- the tension level determines the amount of force
- force gets the nominal value of 1.61 ...
Combining the nominal values of 1 + 1 + 1 + 1.61 + 1.61 .. = 6.2(8) , in radians the vaue is a full circle. Multiplying the full circle 6.2(8) radians by the golden ratio of 1.61 ..
6.2 x 1.61... = 10
we are in ten number decimal system and all the tensions (stresses) beeing calculable at each other. EP-calculation is not decimals, such as none of the calculated loads are not exact. In addition to the above five loads are separately examined in ...
14. YOUNG'S MODULUS OF ELASTICITY
 The Young's modulus (of elasticity) E describes the amount of deflection under load. The modulus of elasticity is placed in the deflection formula as divider => the higher the modulus of elasticity value, the less the material bends. The Young's modulus (of elasticity) E describes the amount of deflection under load. The modulus of elasticity is placed in the deflection formula as divider => the higher the modulus of elasticity value, the less the material bends.
A common modulus of elasticity of steel is 21 000 kN/cm2. The modulus of elasticity has in literature two used values of 20 600 and 21 000 kN/cm2. This calculation and tables use the lower value that gives 1% higher deflection. Both values are sufficiently accurate, but we are planning for a safer side, where the calculation is used for the design.
When designing the deflection, it is determined by the profile cross-sectional shape. This means the same deflection to different grade of steels. The strength of steel has the importance when achieving a lightweight structure. This is achieved by allowing greater local stresses => the higher deflection. Calculation is based on the steel manufacturer's guaranteed yield strength for special steel and when standard steel for the tabulated values. Practical grades of steel are the S235 and S355, which have a wide range of dimensions. Steel product catalogs act as guides for the selection of steel. The elastic limit of steel is between the range of the yield strength and proportionality limit. The limit of proportionality is the first part of a load-elongation curve. The elongation increases in proportion to an increase in tension. When tension reaches the yield limit, elongation continues from here on more than the increase in tension. Above the elastic limit, it will remain a permanent deformation.
kN/cm2 N/mm2 GPa
Aluminium 7000 70 000 70
Concrete 1 000 - 4 000 10 000 -40 000 10 - 40
Duralumin 7 400 74 000 74
Silver 8000 80 000 80
Invar 14 600 146 000 146
Iridium 15 600 156 000 156
Ice - 4o C 1 000 10 000 10
Cadmium 5 100 51 000 51
Copper 12 000 120 000 120
Glass 7 200 72 000 72
Natural rubber (caoutchouc) 5 50 0,05
Brass and Bronze 10 300 - 12 400 103 00 - 124 00 100
Nylon 200 - 400 2 000 - 4 000 2 - 4
Steel 21 000 210 000 211
Titanium 10 500 - 12 000 105 000 - 120 000 105 - 120
Diamond 105 000 - 120 000 1 050 000 - 1 200 000 1050 - 1200
Oak along the grains 1 100 11 000 11
Tungsten 40 000 400 000 400
Tungsten carbide 45 000 - 65 000 450 000 - 650 000 450 - 650
1 Pa = N / m2
Finally
- Of stronger material manufactured part can be loaded with a greater force.
- Strength does not have stiffness => another increase, also another grows. As a result of this analysis has a mathematical possibility, while maintaining the proportionality of load conditions, and comparable materials.
- The modulus of elasticity is a divisor in the formula => to reduce the deflection, must choose the larger cross-section of the same material or a material change to a higher elastic modulus. (868)
15. AN OTHER WAY CALCULATE THE STRENGTH OF MATERIALS
Steel needs the topic mentioned procedure, difffering from arithmetics. Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used very popularly, for tasks ranging from simple day-to-day counting to advanced science and business calculations. Now we start phi and pi calculation. If pi (3.14) is to you the ratio of a circle's circumference to its diameter, the view of the strength calculation is narrow sighted. The above was observed the nomilal tension (stress) values formed the full circle (angle) of 6.28 radians. The value of pi 3.14 is the half of the whole. We use the value of pi when some touchable things we know, the less known side of the pi are the untouched issues such as the stresses in the steel are invisible
Visual Geometry
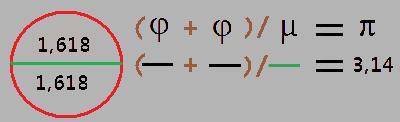
Golden Ratio + Golden Ratio + Golden Ratio + Golden Ratio /Univeral friction = Full angle 6.28 radians.
1.618 + 1.618 + 1.618 + 1.618 / 1.03 = 6.28 rad
1.618 + 1.618 / 1.03 = 3.14 (pi)
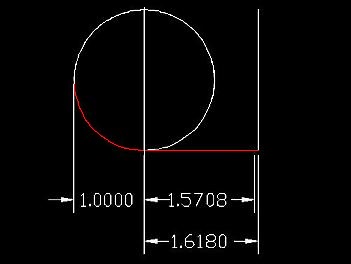
1.25 x 1.25 = 1.57
1.57 x 1.03 = 1.618
1 = something what exists 0.25 = factor => factor 1.25 to calculation
(Note the five steps) (890)
Time dilation table
16. LOAD AND FORCE 1 KN
 In principle strength of materials requires one load 1 kN. In spoken language it is roughly 100 kg, but in physics 100 kg mass. In the strength of materials, load and weight are relative to 1 kN load or force. This is the weight of many of us carrying something with or after weight loss. The load 1 kN is marked using big F letter and with the multiple after it. In principle strength of materials requires one load 1 kN. In spoken language it is roughly 100 kg, but in physics 100 kg mass. In the strength of materials, load and weight are relative to 1 kN load or force. This is the weight of many of us carrying something with or after weight loss. The load 1 kN is marked using big F letter and with the multiple after it.
F1 = 100 kg F10 = 1 000 kg
F05 = 50 kg F01 = 10 kg
Now there is an image of the load. The load F is compared to the calculated load, although that would be hundred times bigger than the compared load.
Load 1 kN is marked F1 and to the same extent 5000 kg load is marked F50. The load F50 comparing to the load F1, makes the calculation proportional. We do not calculate, we compare tensions, deflection and other values. This makes the calculation fast and easy to solve tasks.
Proportionality also calculates often the complex, which by the traditional way, would take an "eternity". Sometimes the traditional calculation can not it, the EPC is capable. Loads are either real loads or nominal in connection to strength of materials. Everything in the real world has its opposite thing, so also in this the non-material and material face each other.
Calculation is possible with this kind of arrangement and also Pasca's triangle has connection to the calculation. In calculation we count potency number and look the result either from some table or on the calculator. I had already a idea of this kind calculation, until I heard some engineer in big office saying; "I am not able to calculate strengths, but when I walk on the construction, I am able to say, is the structure strength enough". This finally confirmed me the calculation principle.
16. STANDARD NUMBERS
 Pythagoras identified in music the scale relationships that work as an introduction to EP-calculation. Also technical design is based to "musical scale of engineering ", referred to as the standard basic sets of numbers. The standard basic sets of numbers are based on same idea than Archimedes' "Golden Rule of Balance", the lever arm length. The further away some value is from the smaller, the higher the value is compared to smaller. Pythagoras identified in music the scale relationships that work as an introduction to EP-calculation. Also technical design is based to "musical scale of engineering ", referred to as the standard basic sets of numbers. The standard basic sets of numbers are based on same idea than Archimedes' "Golden Rule of Balance", the lever arm length. The further away some value is from the smaller, the higher the value is compared to smaller.
The following are two definitions of the standard numbers, one of which is SFS standard and the second DIN standard. It is the same. It is elapsed time since about 2.500 years from Pythagoras times.
SFS 2964 standard 1973
"The standard numbers are to streamline and facilitate the magnitudes of free choice of the values. Standard numbers are applicable for any quantity at and are also used for other than standard parts. Additional numbers be exercised only when a specific reasons."
The above is a clear guideline to follow standard numbers. Have we passed the instruction and ignored it? Have we perhaps unknowingly used the ratios? This occurs eg. when dimensioning steel profiles and the various components are based on the standard numbers.
The above is a clear guideline to follow standard numbers. Have we passed the instruction and ignored it? Have we perhaps unknowingly used the ratios? This occurs eg. when dimensioning steel profiles and various components that are based on the standard numbers.
An example of HEA cross-section
1 - 1.25 - 1.6 - 2 - 2.5 - 3.15 - 4 - 5 - 6.3 - 8 - 10
HEA 100 120 160 200 240 300 400 500 600
The same when some other cross-section. Later we calculate the before showed.
Conveyor belt widths in mm.
1 - 1.25 - 1.6 - 2 - 2.5 - 3.15 - 4 - 5 - 6.3 - 8 - 10
300 400 500 650 800 1000
1200 1600 2000
Metric screws (mm)
1 - 1.25 - 1.6 - 2 - 2.5 - 3.15 - 4 - 5 - 6.3 - 8 - 10
M1,2 M1,6 M2 M2,5 M3 M4 M5 M6 M8 M10
M12 M16 M20 (M24) M32 M42
DIN 323, DIN 3
"Normal numbers are used in machinery and equipment to set selections, prescribing pressures, revolution, peripheral speed, powers, and similar variables as well as numerical values of length to machine parts." As a general rule the dimensions must comply with the basic procedures without compromising the appropriateness of technical features or without wasting possible raw material.
Basic Series R 5 The standard numbers are rounded values of geometric series of consecutive terms. Selected sets are the fifth root of ten (R 5 = 1.6), the tenth root of ten (R 10 = 1.25), the twentieth-root of ten (R 20 = 1.12), and the fortieth root of ten (R 40 = 1.06). The numbers based on the standard series R 5, and R 10 have a large effect on product design. The standard series factor can be checked by multiplying five times 1.6:
1.6 x 1.6 x 1.6 x 1.6 x 1.6 = 10.(486)
1 – 1.60 – 2.50 – 4.00 – 6.30 – 10
1.65 = 10
1.2510 = 10
1.1220 = 10
1.0640 = 10
(1.0380 = 10)
Basic Series R 10
One or two set of standard numbers can not be explained the engineering design in practice, but it can model. The basic set of standard numbers R 5 is too few to product design.
Therefore, the standard numbers for the basic set of R 10 complete the set of R5, including the factor 1.25. Factor 1,25 is good for a number of products. Also to structural analysis, as well as machinery ageing, so it can say 1.25 is a major factor.
1.00 – 1.25 – 1.60 – 2.00 – 2.50 – 3.15 – 4.00 – 5.00 – 6.30 – 8.00 – 10.00
Basic series R 20
1.00 – 1.12 – 1.25 – 1.40 – 1.60 – 1.80 – 2.00 – 2.24 – 2.50 – 2.80 – 3.15 – 3.55 – 4.00 – 450 – 5.00 – 5.60 – 6.30 – 7.10 – 8.00 – 9.00 10.00
The basic set R 20 of standard numbers is too dense to product design, product variations, because the number becomes large, but it is perfect for goods, such as pipes, etc.
Wheel diameters to crane end carriages
1 - 1,25 - 1,6 - 2 - 2,5 - 3,15 - 4 - 5 - 6,3 - 8 - 10
125 160 200 250 315 400 500 mm
Basic series R 40
The basic set of R 5 is preferred before R 10 series and the same when R10 to further R 20 series, etc. The series below is as the previous R 20 series, which we do not use for the EP-calculation. The product designer must be aware of the standard number series, because EP-calculation is largely based on the standard numbers.
1.00 – 1.06 – 1.12 – 1,18 – 1.25 – 1.32 – 1.40 – 1.50 – 1.60 – 1.70 – 1.80 – 1.90 – 2.00 – 2.12 – 2.24 – 2.50 – 2.65 – 2.80 – 3.00 – 3.15 – 3.35 – 3.55 – 3.75 – 4.00 – 4.25 – 4.50 – 4.75 – 5.00 – 5.30 – 5.60 – 6.30 – 7.10 – 8.00 – 9.00 – 10.00
(For example outside diameters of tubes and pipes in mm)
The Use of Basic Series
Standard numbers based on a series of R 5, has well-proportioned aspect ratio of 1.6. This can be checked by measuring one of the room length and width. Also, the face height and width ratio of 1.6 is considered pleasant. Measure the width and height of the head and you notice this.
Series R10 supplement form, which is raised in strength calculations. The designer does the work of strength and deformation, in addition planning the object to withstand corrosion and fatigue. Product Designer is not a designer, but a properly determined is often pleasant to the eye.
Design a whole having the ratio from 1.25 to 1,6(18 the golden ratio). Check out the product catalogs and identify steels and components having the ratio. By this way steel sections and components are guiding proportions. (897)
17. PRODUCT VALUE SPACE
The idea of the value space concept was developed in the context of the design of products. This, using a systematic design methodology to complete product families. I designed the products using a computer since the early 80s. At first the small computer programs, outputted a coherent whole.
The concept of the Product Space Value is necessary for the calculation. This is based on the law of the universe, and this also joined to the engineering. The idea of a separated universe in the machine building universe, is a dead duck. In physics, we can change the values of different units, the Proportional Equivalent Calculation without getting covered. Only in the case of gravity, science is powerless to explain it. The Equivalent Proportional Calculation is based largely on gravity, still attempting to explain the phenomenon. Much of its nature may, however, find the calculation. In addition to experience we need something to detect the reflected information from the Product Value Space. I developed the software for this purpose that collects and produces knowledge of product design. The procedure collects the dispersed information and centralizes the collected information to create new knowledge. The Equivalent Proportional Calculation has born by this procedure. The calculation based on products is a fact that can not be denied. Following from this is a equal procedure to the physiology and physics. (220)
18. GRAVITATIONAL FORCE
Deflection is the shadow of a loading. We know or assume irrationally commercial products to be straight. Direct or spatially planar surface is difficult to establish on earth. With the help of the Equivalent Proportional Calculation, is possible to define deflection and much more. Deflection of the physics, physiology and strength are finally equivalent, in other words same meaning. Deflection has names like time dilation, ageing and fatiquing. In this context staying in steel, gravity stays behind the phenomena. Ground pulls everything to Him.

The shadow of a load deflection
Without the force of gravity, nothing does bend or tire when loaded. All would float in the weightless space, neither would be the friction. Friction is wider concept than friction between two surfaces. Friction affects to everything and we calculate tasks using Universal Friction 1,03(3). Otherwise, we do not have the ability to these calculations.
Pentagon describes the force of gravity g on the Earth
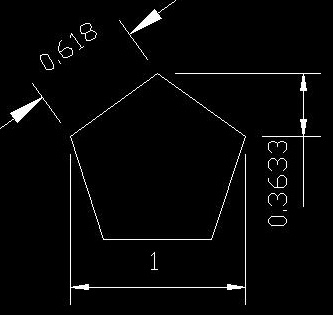
0.618 + 0.3633 = 0.9813
Value 0.9813 is the Force of Gravity 9.82 m/s2. The proportional Equavalent Calculation is not formulas, and please do not consider decimals. Please think, how simple way the nature presents the force of gravity. (605)
2 pii rad x 1.252 = 6.28 x 1.252 = 9.813
19. HOOKE'S LAW
The elongation is directly proportional to the tensile force and the length of the bar and inversely proportional to the cross-sectional area and the modulus of elasticity.
In the elastic range of a material, strain is proportional to stress.
F <=== ========== ====> F
F ===> ========== <==== F
Hooke's experimental law may be given by:
Lσ = F x L0
A x E
Lσ = Extension of a bar
σ = tension in general
F = force producing extension (kN)
L0 = original length of a bar
A = cross-sectional area of a bar (cm2)
E = elastic constant of the material, the Modulus of Elasticity, also named Young's Modulus (20 600 kN/cm2)
Example 1
A = 1 cm2 L0 = 100 cm F = 1 kN
Lσ = F x L0 = 0.00485 cm
A x E
Example 2
How much is the steel bar strain having a cross-sectional area of 12 cm2, when a length of 18 meters and a force of 42.5 kN.
a)
Lσ = 42.5 x 18 x 0.00485 cm
12
Lσ = 0,31 cm
b)
Lσ = 42,5 x 1800 cm
12 x 20600
Lσ = 0,31 cm
Tensile Stress
Tensile stress, or simply stress, was equated to the load per unit area or force applied per cross-sectional area perpendicular to the force measured in kN force per square cm2. Original units were different, but Hooke's idea was the same in 1687.
The load per unit area
σ = F
A
Example 1
42.5 kN normal force affects to 12 cm2 cross-sectional area. What is the tension?
σ = F
A
σ = 42,5 kN
12 cm2
σ = 3,54 kN / cm2
ε (epsilon) Elongation of the rod when squeezed or pulled
ε = Lσ / L0
ε = 0,31cm / 1800 cm
ε = 1,719 x 10-4
σ = ε x E
σ = 1,719 x 10-4 x 20600 kN/cm2
σ = 3,54 kN/cm2
Tensile strain of a bar per unit length
ε = σ / E
For the equations described above expressed by Hookes Law for elastic materials. For materials under tension, strain (ε) is proportional to applied stress σ. Removal of the stress results in a gradual return of the metal to its original shape and dimensions.
21. FREE FALL OF A BODY
Deflection rate 1:1000 is the basic beam stiffeness of bending and values can calculate from strength calculation to Physics and contraversary. As an example the static values of round bar 10 mm (1 cm). Imagine to the photo a round bar. The size of 10 mm has the basic values to determine values of all others.

Taipuma 1:1000 Deflection
As a part of Visual Geometry
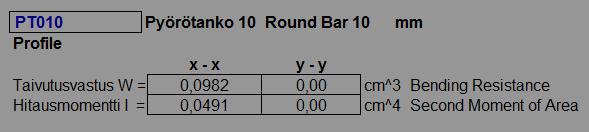
0.0982 cm x 100 = 9.82 m/s2
Gravitation on the Earth.
0.0491 cm x 100 = 4.91 m
Free fall per one second on the Earth
You can see the connection of round bar values to the free fall of a body. All is free fall of a body, its prevention or friction to prevent falling in motion. This is why, all are the same meaning. (661)
Physics - Physiology - Matter and Strength
As a Visual Geometry
22. CIRCLE AND SQUARE AREAS
Visual geometry is the way to calculate the geometry of the phenomena, in which physics recognized values revolve around to shapes and areas. The force of gravity has not previously been treated in a manner as in this context.

Circle's surface area 0.785 units
In the photo there are two steel rods of cross-sections a square and circle. Cross-sections of the bars have proportion to gravity acceleration and time dilation. Nominal rod dimensions are 1 to both rods, without significance of the units. By calculating the circular surface area, the square surface area is known and vice versa. The speed of light as an intangible 0.25, corresponding to the material world, a factor of 1.25.
=> A = 0.785 x 1.25 = 0.981 (gravity acceleration 9.81 m/s2)
A = 0.785 x 1.25 x 1.0328= 1.0 (square area)
Visual geometry notes the value of gravity acceleration (9.81 m/s2) and time dilation (1.0328). Calculation sets the same meaning between the surface area and gravity acceleration. Visual geometry is a way of approaching things and phenomena through patterns and areas. This may proceed through proportionality to strength of materials and as well to assess human performance. (1085)
An example
 a) The gravity value of 9.82 m/s2 consists of the material (distance m), and non-material (time). These together form the conceptual area 9.82 x 9.82 = 96.43 (ms)2. The strength is often expressed, for example, as allowable tension 14.6 kN/cm2. The entry contains in the pressure, expressed in a similar manner to pressure vessels. Units varies, but the purpose is the same. We are approaching to the same meaning calculation called EP-calculation. a) The gravity value of 9.82 m/s2 consists of the material (distance m), and non-material (time). These together form the conceptual area 9.82 x 9.82 = 96.43 (ms)2. The strength is often expressed, for example, as allowable tension 14.6 kN/cm2. The entry contains in the pressure, expressed in a similar manner to pressure vessels. Units varies, but the purpose is the same. We are approaching to the same meaning calculation called EP-calculation.
b) Let us think you are a farmer. You have small one acre (100 m2) farm, where you are growing the force of gravity. Gravity stopps the motion through the friction and bends the materia. Gravity is well selling product in the market. One day you buy new seeds for the crop. The need is 0.01 kN per square meter, so you need 100 kg of seeds. After weighing, the merchant adds a handful of extra seeds into the bag. Your purchase weighs now 101.8 kg. When sowing the seeds into the field, you notice one part of the field to be in poor condition, so it will not get seeds. Hundred square meters of surface area has now decreased to 98.2 square meters of surface area. Still you sowed all the seeds evenly into the good part of field.
Now you get by calculating the weight per square meter 101.8 kg/98.2 m2 = 1.03 kg/m2. Although the need was 0.01 kN per square meter, but you have not put too much seed, because all the seeds will not germinate. The not germinated seed corresponds in physics the friction that stops the motiona. Friction value of 1.03(28) is required for the calculation in phenomena. In principle, the farmer and the strength calculator, do the same having different names. Perhaps the following calculations? Structural analysis is physics, the physics is time and energy, which ultimately leads to energy formula. The speed of light and time dilation are one part of strength of materials, but so far unknown subsystem. Everything is finally lengths, surface areas and volumes, which involves time as an integral part. (858)
96.43 (ms)2 x 1.018 kN = 98.2 m/s2
101.8 kg / 1.03(4) friction = 98.2 m/s2
24. SPECIFIC GRAVITY OF STEEL
24.1 Circle and Ellipse
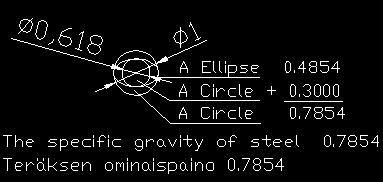
The area of unit circle (1) determines the specific gravity of steel (0.785). Ellipse and circle patterns inside the circle, have between them the golden section proportion, determine the mechanical properties of steel. This is a simple summing function.
0.3000 + 0.4854 = 0.7854
1,618 x 0,3000 = 4.854
24.2 Steel Unit Circle and Aluminium
The material of the calculation is steel. The steel is in connection with Big Bang, containing the calculation base.
Steel unit circle; diameter one unit and length one unit
a) the specific gravity of iron is 7, 87 g/cm3.
b) the steel is iron, from which is taken off some coal. Carbon steel has a few percent, and the specific gravity value of 7.87 g/cm3 is functional.
The specific gravity of the steel and the unit area of the circle can be measured using coefficient 1.618 and 1
6.181 x 1.618 = 10 = 0.6181 x 1.618 = 1
Units of the calculation does not matter, because they are invented by humans. In this case, the program calculated the weight in grams and lets think the numbers to values of 0.6181 and 1. This is a good workout at the same values. Calculated do not have to be steel. We will calculate the weight of a piece of aluminum plate on the basis of the specific gravity of steel. Specific gravity of aluminum is 2.7 g/cm3.
1.618 / 0.618 x 1.034 = 2.70
Calculation through gravitation 9.82 m/s2
1.618 /(0.618 x 9.82) x 1.034 = 0.275
We go through the whole mathematical palette, from a piece of steel as shown, and we stop to values of the final product formation. This only requires patience and logic simplification. How necessary is to calculate the weight of aluminum, as shown, is another story. (209)
25. FORCES IN A MATTER
 Before start to calculate forces in a matter, it is convenient to be familiar with the forces. Before start to calculate forces in a matter, it is convenient to be familiar with the forces.
 25.1 Compression 25.1 Compression
When compressing the material, there will be the compressive stress generated. In the photo, the vertical timber is under the compressive loading.
==> <==
25.2. Pulling
When pulling the matter, there will be a tensile stress generated. In the photo, the horizontal timber of truss receives a pulling force.
<==>
25.3 Bending
When bending the matter, there is a tensile stress generated. In the photo the timber for the window opening, has a high probability of bending under the influence of the load.
II F
========================
/\ /\
25.4 Torsion
When twisting a matter there will be a torsional stress. Power shaft is an example of this.
=========
25.5 Shearing
When cutting a matter, there will be a shearing stress generated, An example is cutting paper with scissors or a shaft stresses due to torsional loading.
==> II
II <==
There are five are pure forces, and then force combinations.
25.6 Swinging as a Force Combination
When bending a matter and at the same time having a torsion, the body swings. The cantilever supported, impacted at its end a force or forces.
II II II F
===========================
II II
25.7 Buckling as a force combination
When compressing the rod like body, there will be a compressive stress generated and the rod bends to side. Having a certain force, the body loses the stability and buckling happen. In the photo the vertical timber has the compressive tress and the buckling can happen..
25.8 Plate Buckling as a force combination
Such an event, the buckling of the plate-shaped part. (217)
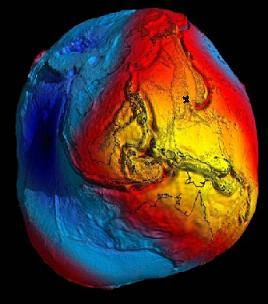
30. MAGNITUDE OF GRAVITY ON THE EARTH
Variates and this is reason why the gravity acceleration g 9,82 m/s-2 has in literature different values. I am living there were is the cross marking in the photo. Yellow areas have a low magnitute and Ocean areas (blue coloured areas) have the highest magnitude. You remember the mention of round shapes like a ball or the Earth, if they have round shape, and to what extent? We had the round shaped two-dimensional area through unit circle. This indicated the specific gravity of iron. Then we have the three-dimensional ball to indicate through the press marking the hardness of the tested steel. Both are based on the area.
g = Acceleration of free fall 9,82 m/s2 when a falling body
(The speed of light (E = m) c2 and acceleration of free fall s2 are both areas)
31. SHADOW OF THE BENDING
The loaded girder can be pre-calculated, deflection, stresses etc. We use to like the calculation result as axiom. Still, however, there is no long time as the strength calculation was not possible. Thinking about the matter, the deflection shadow is caused by the load. This shadow under beam can see in the bigger image. It depends on the direction of the light, whether to see the shadow of the deflection or not. Issues in the analysis is the same, depending on the viewer's point of view under review.


The force of gravity bends the beam, whereby in many meanings, it is question of the power. In connection with the power, it is often used the name of energy. The energy conversation is known, but has bending the parallel meaning to other matters? Shadows generally are something that cannot touch as the calculation result, as can not touch any energy. Of these shadows, is partly ask on my pages. (995)
32. SHADOW BEHIND THE PASCAL'S TRIANGLE
1. Shadows in the EP-Calculation
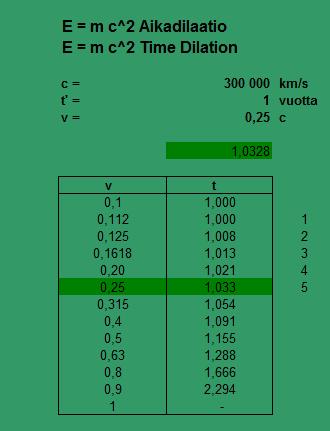
In the calculation the term "shadow" means something real generated value, which is invisible. The value can be displayed by exposing the shade by the possibility of EP-calculation. Albert Einstein brought this opportunity to the theory of relativity in the formula
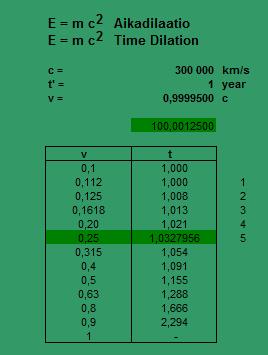
E = m c2
Momentum p is transformed into Lorenz - variant factor 1/L when L = sqrt (1-( v/c )2)
==> time dilation 1.0328 when the speed of light 0,25 c
1d x 2d x time dilation = 1.618
1.25 x 1.25 x 1.0328 = 1.618
1d x 2d x 3d x time dilation = 2
1.25 x 1.25 x 1.25 x 1.0328 = 2
1d = one-dimensional diameter
2d = two-dimensional cross-section
3d = Three-dimensional object
We are living in 3d-world, so the Pascal's triangle row factor
1.1 = 1.03283 = 1.1
2. Pascal's Triangle Behind It All
We pay a visit behind the Pascal's triangle, by visual geometry and calculator. The following Pascal's triangle is logical until the fifth row, but does not forward. The fifth row is the proportionality limit in phenomena, so Pascal's triangle is logical in this sense. The calculator gives for the sixth row the value 1.1 x 1.4641 = 1.61051. The sixth row corresponds to the value of golden ratio 1.61 (8), which importance to the phenomena has remained to EP- calculation. Let us do a calculation, where the length of the girder increases 1.1 times the relative length of 1.4641. Both the starting rows are shown in bold below in the triangles ( HEB 100, and Pascal's triangle) .
1.1 x 758 cm =834 cm
1.1 x 834 cm = 918 cm
3. LOAD 1 KN
The calculation load is only 1 kN, which is approximately 100 kg. The load is small, so that it corresponds to the weight of a person. After this the phenomena can cross-calculate with steel and physiology. After all, the principle of the calculation is the same meaning calculation. When the principle of the calculation is clear, loads and spans can be anything, but not yet at this stage. Therefore, you do not calculate only the strength, but at the same time studying human physiology.

||
|| Forcce 1 kN
\ /
=======================
/\ /\
Deflection of the concentrated force (= load)
4. CALCULATION
4.1 You have the formulas and calculator to calculate deflection of the girders. Before you have calculated deflections of the load and the girder weight, a lot of time has elapsed. Therefore, the girder's own weight are often left out of the calculations. This is an error that could backfire dearly in certain cases.
4.2 EP-calculation does not need formulas, but the calculator is needed. The old calculation method is laborious, and it is not the only option. The EP-calculation takes into account the deflection of the load and the weight of the girder to be born, which is an advanced way to calculate .
4.3 For those whom cannot calculate the deflection through the view of phenomena, the easiest method is to click on the above photo and add the required data to Excel spreadsheet. You can thus look the same, which is shown in the triangle below. The calculation (EX141 1_01) takes into account only the deflection caused by the load.
Length Pascal's Triangle Deflection
HEB 100 -1 1
HEB 100 -1.1 1 1
HEB 100 -1.21 1 2 1
HEB 100 -1.331 1 3 3 1 (factor 1.331)
HEB 100 -1.4641 1 4 6 4 1
HEB 100 -1.61051 1 6 1 0 5 1
HEB 100 - 1.771561 1 7 7 1 5 6 1 1.7367 cm/1.3048 cm = 1.331
918 cm ==================== 1.7367 cm 1.331 jne. - etc.
834 cm ================= 1.3048 cm 1.331
758 cm ============== 0.9803 cm 1.331
689 cm ============ 0.7366 cm 1.331
627 cm ========= 0.5534 cm 1.331
570 cm ======= 0.4158 cm 1.331 x 0.3124 = 0.4158
518 cm === 0,3124 cm -
1.1 Factors 1.331
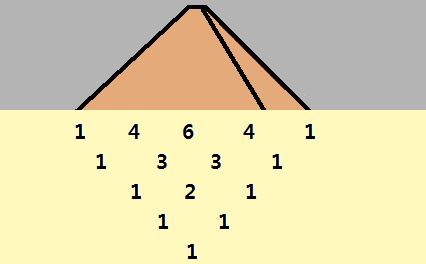
Pascal's Triangle as a pyramid cast a shadow on a row values, which can use to calculate the deflection of the girder, but also other things. This is something that you have probably never done.
33. FOURTH DIMENSIONALITY OF BENDING
Bended girder has three by hand touchable (width - height - length) and one not by hand touchable dimensionality (time).

The dimension of a space or object is informally defined as the minimum number of coordinates needed to specify each point within it.
Let us take an example, the fourth dimensionality is needed. A wooden girder has a nominal load on it. After one year can see what has happened. The wooden girder has a deflection of the load, but the same happens without any outside loal than its own weight. The first three dimensionality are known, but time bends the wooden girder. When steel girder, there is not this feature when proper tension level. Deflection is the shadow of the Fourth Dimension. We can see it, but normally it cannot calculate
In practice, the fourth dimensionality is not necessary to take into account when steel components. Fatiguing has the context to the number of repetitions, but not to the time.
34. BENDING GENERALLY
Without understanding of physics and physiology, does not understand either the nature of the deflection. This is difficult, because physics does not teach the deflection. Deflection is associated with the strength determination, which belongs to engineering education. Deflection is a theoretical subject and the basic element for the best-known energy formula. Energy equations can also be explained through the sport-related issues. Physiological deflection increases the length of time for performance which may indicate as time dilation.
 Basically, deflection causes elongation and shrinkage. The outward manifestation of this is the deformation of the body. In practice saying the object bending. In physics time bends, ie the used time increases. Basically, deflection causes elongation and shrinkage. The outward manifestation of this is the deformation of the body. In practice saying the object bending. In physics time bends, ie the used time increases.
To understand the deflecton, need to know;
a) The number of support points b) How the load is divided - concentrated load - uniformly distributed load (678)
35. STATIC VALUES TO CROSS-SECTIONS
Think the steel profile cross-sections so that you are walking over them and they all seem to bend same like. Select a stronger profile, if it bends more, and the weaker, if the profile does not bend enough. We are all the time at the same deflection ratio. DIN 1025 - Euronorm 53-62 with HEB 100 steel shape is the starting point for the calculation. An example of HEB I-profile, but later the same to other cross-sections.

Bending case 1
Load of 1 kN is the weight of our own, at least the burden on our hands. HEB100 steel cross-section bends 0.518 cm (deflection ratio 1:1000), 1 kN load, the span of 518 cm. These numbers should not look having over-precision.
DIN 1025 - Euronorm 53-62
HEB 100 => F1:1000 = 0,518 cm
In the table are the static values for those who want to check the calculation by the traditional way. The sag of the girder consists of the weight of the girder and load. This is the only way to calculate the actual deflection at one time.
Profile L1000 σt Ix Wx Iy Wy
Nimike cm kN/cm2 cm4 cm3 cm4 cm3 kg/m A cm2
HEB100 518 2.2 450 90 167 33,5 20.4 26
HEB120 644 2.1 864 144 318 52,9 26.7 34
HEB140 761 2 1510 216 550 78,5 33.7 43
HEB160 868 2 2490 311 889 111 42.6 54.3
HEB180 968 2 3830 426 1360 151 51.2 65.3
HEB200 1062 2 5700 570 2000 200 61.3 78.1
HEB220 1150 2 8090 736 2840 258 71.5 91
HEB240 1235 2 11260 938 3920 327 83,2 106
HEB260 1316 2 14920 1150 5130 395 93 118
HEB280 1394 2 19270 1380 6590 471 103 131
HEB300 1468 2.1 25170 1680 8560 571 117 149
HEB320 1534 2.1 30820 1930 9240 616 127 161
The Young's modulus is 20 600 kN /cm2. In the literature also 20 600 - 21 000 kN/cm2. When a value of 21 000 kN/cm2, increases the L1000 length of HEB100 from 518 cm => 523 cm. Bending stress σt remains the same at both values. In practice, the tabled values are the same with both Young's modulus values, because 1% change in values does not mean much. (1054)
36. HEB I-PROFILES STATIC VALUES
Wide-flanged I-beam DIN 1025 - EN 10034, in particular, the size of HEB 100 is used for the various comparison. The profile sizes are at the same calculation factors.
1.00 - 1.25 - 1.60 - 2.00 - 2.50 - 315
HEB 100 - 120 - 160 - 200 - 240 - 320 Size
1. 2. 3. 4. 5. Factor (1.06)
1,00 - 1,25 - 160 - 2,00 - 2,50 - 3.15 - 4.00 - 5.00 - 6.30 - 8.00 - 10.00 (F kN)
1. 2. 3, 4. 5. 6. 7. 8. 9. 10. (1.1)
Ix Wx Iy Wy A
Item cm kN/cm2 cm4 cm3 cm4 cm3 kg/m cm2
* HEB100 518 2.2 450 90 167 33.5 20.4 26.0
1. HEB120 644 2.1 864 144 318 52.9 26.7 34.0
HEB140 761 2 1510 216 550 78.5 33.7 43.0
2. HEB160 868 2 2490 311 889 111 42.6 54.3
HEB180 968 2 3830 426 1360 151 51.2 65.3
3. HEB200 1062 2 5700 570 2000 200 61.3 78.1
HEB220 1150 2 8090 736 2840 258 71.5 91.0
4. HEB240 1235 2 11260 938 3920 327 83.2 106.0
HEB260 1316 2 14920 1150 5130 395 93.0 118.0
HEB280 1394 2 19270 1380 6590 471 103.0 131.0
HEB300 1468 2.1 25170 1680 8560 571 117.0 149.0
5. HEB320 1534 2.1 30820 1930 9240 616 127.0 161.0
The table is read so that on the left is the profile size (height), for example HEB100.
HEB100 span of 518 cm indicates the profile's deflection ratio 1:1000, when the girder has in the middle of it a concentrated load (point load) of 1 kN (102 kg). Deflection is then 518 cm/1000 = 0.518 cm
Similarly, HEB320 beam has deflected 1.53 cm, and the span of 1534 cm (15.34 meters). Tension level kN/cm2 is in both cases 2.1 -2.2 kN/cm2. You are familiar with the other values in the table. Bending formula does not ask the cross-section shape, so any shape can take.
Deflection ratio 1:1000

Bending case 1
Concentrated load 1 kN
* Profiles cross-sections are in dwg. format. The drawings can be opened with freely available software. These can use to 2-dimensional and 3-dimensional drawings.
The table above can think that way. Your weight is 1 kN, which is 102 kg and you are crossing the river, with a width of 14 meters. You will need a suitable support profile for the crossing. Then you can well imagine that the profile HEB280 is appropriate, as it has tabled span of 14 meters (1394 cm) having 1:1000 deflection ratio. Suitable bridge for walking can certainly bend more, in which case the example illustrates the magnitude of which the more accurate examination starts. Later, all loads are derived from the values in the table, not only to a single profile, but to all profiles and loads. (1034)
37. HEB CROSS-SECTION AREAS
HEB is a cross-section of the calculation, which shows other similar cross-section characters. This is visual geometry and needs not to calculate. You observe the similarity between the ratio sequence and cross-sections of the profiles. This is later the the way to calculate strength and determine products. (1049)

1.00 - 1.25 - 1.60 - 2.00 - 2.50 - 3.15 - 4.00 - 5.00 - 6.30 - 8.00 - 10.0 -12.5 - 16.0
A cm2 26 - 34 - 43 - 54.3 - 65.3 - 78.1 - 106 - 131 - 161
Nimike cm kN/cm2 cm4 cm3 cm4 cm3 kg/m A cm2
HEB100 518 2.2 450 90 167 33.5 20.4 26
HEB120 644 2.1 864 144 318 52,9 26.7 34
HEB140 761 2 1510 216 550 78,5 33.7 43
HEB160 868 2 2490 311 889 111 42,6 54.3
HEB180 968 2 3830 426 1360 151 51.2 65.3
HEB200 1062 2 5700 570 2000 200 61.3 78.1
HEB220 1150 2 8090 736 2840 258 71.5 91
HEB240 1235 2 11260 938 3920 327 83.2 106
HEB260 1316 2 14920 1150 5130 395 93 118
HEB280 1394 2 19270 1380 6590 471 103 131
HEB300 1468 2.1 25170 1680 8560 571 117 149
HEB320 1534 2.1 30820 1930 9240 616 127 161
38. HEB I-PROFILES 1 KN LOAD BEARING
European wide flange beams DIN 1025 - EN10034
1.1 Tabled Span when Deflection Ratio 1:1000
L cm Load 1 kN
HEB100 518 The known length when deflection ratio 1:1000
HEB120* 644 1.25 x 100 = 125
1.25 x 518 cm = 647 cm
HEB140 761 span 761 cm when deflection ratio 1:1000)
1.12 x 647 cm = 724 cm
HEB160 868 1.25 x 125 x 1.03(28)** = 160 mm
1.25 x 647 x 1.03 cm = 833 cm
1.25 x 1.25 x 1.0328 = 1.618
HEB180 968 span 968 cm when deflection ratio 1:000
1.12 x 833 cm = 933 cm
HEB200 1062 1.25 x 160 = 200 mm
1.25 x 833. cm = 1041 cm
HEB220 1150 1.12 x 200 = 220 mm
1.12 x 1041 cm = 1166 cm
HEB260 1316 (240 + 260) /2 = 250 = 1.25 x200
1.25 x 1041 cm = 1301 cm
The calculation is so far the accurate
________________________________________________________________
* The standards do not recognize the size of 125 mm, so this corresponds to size 120 mm. I-profile height of 120 mm is smaller than the height 100 mm x 1,25 = 125 mm. Despite of this, the span length error is only 3.5 cm, the proportional error of 0.0054.
** The Universal friction coefficient in other words time dilation factor 1.0328 when the speed of light 0.25 x c, cannot have many decimals in these kind of calculations, so the two decimals precision is enough.

Load 1 kN
2. Proportion Numbers
1 - 1.03 - 1.06 - 1.12 - 1.25 - 1.6 - 2 - 2.5
3. Standard Numbers
100 - 125 - 160
4. The Fifth Row of Pascal's Triangle
1.4641 x 1.1 = 1.6105
5. E = m c2
Momentum p is transformed into Lorenz - variant factor 1/L when L = sqrt (1-( v/c )2)
==> time dilation 1.0328 when the speed of light 0.25 c
1d x 2d x time dilation = 1.618
1.25 x 1.25 x 1.0328 = 1.618
1d x 2d x 3d x time dilation = 2
1.25 x 1.25 x 1.25 x 1.0328 = 2
1d = one-dimensional diameter
2d = two-dimensional cross-section
3d = Three-dimensional object
We are living in 3d-world, so the Pascal's triangle row factor
1.1 = 1.03283 = 1.1
6. Dimensionalities in the Calculation
1
1d 1 1 Length
2d 1, 2 1 x 1,03 = 1,25 Surface
Pascal's Triangle
Surface factor x Fatique factor = General Fatiquing Factor (Universal friction) (1144)
39. Static Values of the Wall Thickness
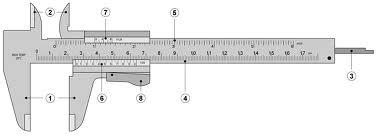 This continues the calculation of the wall thickness and different static values. We need for the calculation one slide calliper and calculator. In stock there is a hollow section tube 200x200x5, but its static values are not known. The slide calliper is needed to check the wall thickness 5 mm and tube outside dimensions 200 mm. This continues the calculation of the wall thickness and different static values. We need for the calculation one slide calliper and calculator. In stock there is a hollow section tube 200x200x5, but its static values are not known. The slide calliper is needed to check the wall thickness 5 mm and tube outside dimensions 200 mm.
The idea is there that sometimes the section has no static values. The simple example is the hollow tube section. That we know is the weight 88,4 kg/m to tube 200x200x12,5. How about the weight to tube 200x200x5?
Time Dilation

Most have never calculated time dilation. The well known is that all originates from the energy bubble long time ago. That is why to calculate through the energy, and is the reason why the table above in on the page. In others cannot calculate things having the same meaning. The table is also used to the curvation of space-time and the mass weight changes calculations. This means, the large-scale phenomena is included into the small-scale phenomenon.
The Weight of the tube 200x200x5
Item Weight kg/m Calculated weight kg
Tube 200 x 200 x 5 38.1 88.4/1.254 x 1.033 = 37.4
Tube 200 x 200 x 6,3 47.4 88.4/1.253 x 1.033 = 46.8
Tube 200 x 200 x 8 59.2 88.4/1.252 x 1.033 = 58.4
Tube 200 x 200 x 10 72.6 88.4/1.25 x 1.033 = 73.1
Tube 200 x 200 x 12,5 88.4 The known value
Cross-sectional Calculated area
Item tabled area cm2 cm2
Tube 200 x 200 x 5 29.9 69.4/1.254x 1.033 = 29.4
Tube 200 x 200 x 6.3 37.2 69.4/1.253 x 1.033 = 36.7
Tube 200 x 200 x 8 46.5 69.4/1.252 x 1.033 = 45.9
Tube 200 x 200 x 10 57.0 69.4/1.25 x 1.033 = 57.4
Tube 200 x 200 x 12.5 69.4 The known value
The commercial steel tube wall thicknesses, consists of the ratio numbers to EP-calculation.
1.25 - 1.6 - 2 - 2.5
6.3 - 5.0 = 1.3 mm (1.25)
8.0 - 6.3 = 1.7 mm (1.6)
10.00-8.0 = 2 mm (2)
12.5 - 10.00 = 2.5 mm (2.5)
40. Allowable Stresses, Steel
Calculation has the idea, by knowing the loading case, the other 20/80 rule, are known. Size of the load (the arrow size) or load (arrow) location may vary. The load may become uniformly distributed load on the beam and the profile may change, as well as the number of support positions. Nevertheless, in a simple manner is known the change of values. Calculation is not possible without understanding of the forces in a matter.
 The basic bending case: Concentrated load effects in the middle of the girder which is supported at the both ends. Deflection consists of the concentrated force in the middle of the girder and of the girder weight. The basic bending case: Concentrated load effects in the middle of the girder which is supported at the both ends. Deflection consists of the concentrated force in the middle of the girder and of the girder weight.
The load and the weight of the girder together cause the bending. The top surface is compressed and lower surface stretched, so the strength analysis of bending is the examination of stresses. At the bottom of girder is the maximum tensile stress and the maximum compressive stress at the top, called for normal stresses.
When the cross section of the girder is symmetrical about its center axis named the neutral axis, the bending stress there is zero. For this reason, drilled holes is preferred to make to middle of the profile, wherein they have no major impact on the strength of the cross-section. This situation arises sometimes when support beams, tubes go through the center of the cross-section. The image girder stresses in the center (vertical energy-level description)
1 (+) - 0 - 1 (-),
meaning => in the middle of the beam, is the smallest normal stress. Where it is a maximum bending stress, shearing stress is at a minimum.
40.1 Magnitude of Stresses
The resulting stresses of the construction are not allowed to become too high, because the risk of failure or excessive deformation. Structure is designed in such a way that the stress does not exceed the allowable stress.
Permissible stresses for static loading is a particular part of the used material breaking strength or yield limit. The yield limit diimensioning is the more used method and according to equivalent proportional calculation. (324)
σ all = σ M / n Dimensioning to the breaking strength
σ all = σ m / n Dimensioning to the yield limit
σ all = Allowed stress
σ M = breaking strength
σ m = yield limit
n = safety factor
40.2 Fatigue Loading
σ all = σ all W / n σ all = σ T / n
σW Endurance limit for reversed stress
σT Endurance limit for pulsating
41. Impact Strength of Steel

Tanker weld fracture (source: http://school.mech.uwa.edu.au).
The impact strength refers to the agreed -shaped specimen and is the capability of the material to withstand a suddenly applied load and is expressed in terms of energy. Therefore, a similar test rods are comparable, because the impact strength is depending on of the rod's shape.The prior piece shape is the Charpy U- rod, a functional test of the pendulum hammer to fracture a sample. To determine the impact strength of the hammer energy losses are divided into the cross-section fraction of the surface J/cm2. Over time, the impact strength of the steel decreases, so that the phenomenon is referred to the aging of the steel. Aging often occurs near the cracks in the weld seams. The fracture occurs sometimes after a short time of welding, sometimes a fracture occurs years later. Cracking occurs particularly in the context of poor grades of steel and has therefore taken into account the impact strength when selecting the steel. The moderate welding qualification requires about 30 .. 40 J/cm2 impact strength - at the structure's operating temperature - the cases requiring up to 80 J/cm2. At this point, the energy can be used to determine the material ability to withstand the occurred impact load. (340)
42. Steel Hardness and the Breaking Strength
Structural steel S235 HB 100...125
1,0 - 1,03 - 1,06 - 1,12 - 1,25 - 1,618 - 2,0 ...
Calculation use the steel intermediate hardness HB 112 kN/cm2 of steel grade S235. This corresponds to the ratio 1.12. In general, structural steels have hardness variation, even in same grade. Hardness is measured by pressing the agreed form of hard piece onto the steel surface. By measuring the born mark, is known the hardness of the steel. Steel is manufactured in different kind of processes. Between different steel grades, the strength variates, which can express as hardness. It has been adapted that the certain level the strength of the steel does not get fall short anywhere in the conditions. This kind of steel can be used to reliable strength calculations. The calculation takes the knowledge of steel characteristics to the next level. This unintentionally, that the calculations are more accurate than the other way. The calculation criticizes only reliable and accurate calculations, which were later to say, oops.
Hardness Comparison
HV HB Breaking strength N/mm2
100 95,0 320 Breaking strength formulation
105 99,8 335 Adapted given value 335 N/mm2
110 105 350
115 109 370
135 128 430 1,25 x 335 x 1,03 = 431 N/mm2
160 152 510
190 181 510
210 199 675_____1,253 x 335 x 1,03 = 674 N/mm2
1,253= 2 ja /and 199 / 99,8 = 2
1 1 2 3
1,25 = 1 1,253= 1,25 - 1,6 - 2,0
128 - 152 - 199 (HB)
The hardness of steel is not a coincidence. By knowing the hardness of steel, this can lead to values. Having become acquainted with the calculation, we calculate from these data, allowed tension values to load cases. We can also estimate the used material and the required size of profile. (932)
42.1 STEEL HARDNESS, THE GOLDEN RATIO
Dividing the circle area by bigger ellipse area, the areas includes the ratio of 1:1.618. The diameter of the circle per the ellipse minor axis length, includes the Golden Ratio. The larger elliptical area per the smaller elliptical area, has also the ratio 1.618.
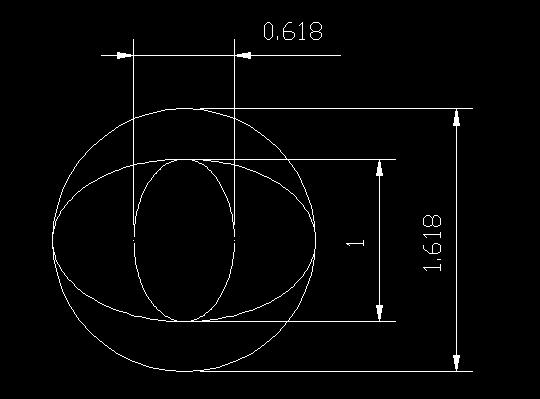
When drawing an ellipse inside the ellipse having the ratio of 1.618, the area is 1:2.618 of the previous ellipse.
1 + 1.618 = 2.1618 1.618 x 1.618 = 2.618
Area of the circle is 2.0561 units The larger ellipse has the area of 1.2708 units => 2.0561 / 1.2708 = 1.618 The smaller ellipse has the area of 0.4854 units => 1.2708 / 0.4854 = 2.618
The circular shape has the hardness of the material, strength ellipses.
Why to do this. This I'll expain through the strength calculation ...
The Golden Ratio joins to machine engineering most common material, steel. However, we do not notice the golden ratio, choosing the quality of steel, or examining the strength of steels. The tensile strength of steel is proportional to the hardness, in a such a way up to 100 kN/cm2, the ultimate tensile strength of carbon steel is 36% and alloy steel 34% of the Brinell hardness. The percentual share has been observed, but not the joining to the Golden Ratio.
The ratio φ (1.618). The ultimate tensile strength of carbon and low alloy steels, can be quite precisely determine by dividing the steel hardness HB by ratio 1.618. => HB 112 / 1.618 = 69.221 => σM = 112 - 69.221 = 42.8 kN/cm2. The value 42.8 kN/cm2 corresponds to S235 steel grade with a guaranteed ultimate tensile strength of at least 37 kN/cm2.
HB = Brinell hardness σM = The ultimate tensile strength
Structural steel S235 HB 100...125
51. AXIAL DEFORMATION
Beam cm
F kN ==> ================ <== kN
Equivalent Proportional Calculation needs the exact known value to know others.
Calculation by formula does not need the exact value.

F = 1 kN L = 100 cm A = 5 cm2 ό = 0,001 E = 20 600 kN / cm4
Basic load 1 kN
Length 100 cm is easy to remenber
Deformation 0,001 cm
F =1 kN L = 100 cm A = 5 cm2 ό = ? (question)
ό = 100 cm x 1 kN x cm2 = 0.001 cm
20600 kN x 5 cm2
By using the formula, can calculate steel deformation, but not understand the calculation. Formula works also to calculation of elongation. (778)
Beam cm
F kN <== ========= ==> F kN
52. AXIAL DEFORMATION OF A BEAM
Axial compressive strain of steel bars will tell you how much length is shortened, or conversely, it will stretch when squeezed or pulled. Power is 1 unit, cross-section of 5 units and 100 units in length. => Relationship between axial compressive strength and the range is 1 / 1000. Relationship exists, others have no known formula. Take a few minutes to think about this. Gravitation is 9.82 m/s2. Calculation uses cm unit. The calculation is based on the Newton - Gravitation - Surface Area - Figure Five combination. One feature of the calculation is the Visual Geometry, which means the figures and calculations are visually shaping the reality. Figure above is a calculation that represents the accession of each other names. At this point, is enough to detect the ratio of the links between them. Eventually, surface area and strength are the same meaning. Axial compression rod is inversely elongation rod. The force is often a value of 1 (.02) kN, which other loads are known. The calculation uses the value 20600 cm4 of the Modulus of Elasticity. (156)

Click on the calculation
53. MISSING MOMENT OF THE WIRE
The thin wire is placed between two points, which represent the points A and B. The wire can be expected to be light, wherein the supporting forces A and B are low.
A = B = G / 2

 So that the light wire does not have any sag on the wire. There is need to have an infinitely great force, relative to size of the wire. The strength of the wire will, therefore, be extremely large in order to take against the pulling force. This situation does not arise in real life. Yet, a similar kind of situation still generated by electrical power lines with wires sagging. The thin wires (ropes) are under tensile stress, but having no bending moment. Wire as a result of lack of rigidity, the wire dimensioning is based on the cross-sectional surface area. So that the light wire does not have any sag on the wire. There is need to have an infinitely great force, relative to size of the wire. The strength of the wire will, therefore, be extremely large in order to take against the pulling force. This situation does not arise in real life. Yet, a similar kind of situation still generated by electrical power lines with wires sagging. The thin wires (ropes) are under tensile stress, but having no bending moment. Wire as a result of lack of rigidity, the wire dimensioning is based on the cross-sectional surface area.
In cross-section with a small section modulus, tensile stress arises in practice. Wire and electric wire rope, have a poor load bearing capacity, not to mention of the pushing, but a large pulling capacity. Pulling forms a tensile stress, whereby the wire dimensioning is a quite simple task.
Pieces having a stiffness => generate a tensile and compressive stress which have opposite signs on opposite sides of the cross-section. In the center is the neutral axis, where the stress is zero.
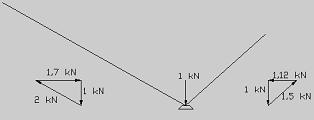 When suspending the roadway lighting eccentrically, it generates the above loading case. Designer's design program makes the determination of forces in the wires to be simple. After this is determined an appropriate safety factor for cable pulsating loads. When suspending the roadway lighting eccentrically, it generates the above loading case. Designer's design program makes the determination of forces in the wires to be simple. After this is determined an appropriate safety factor for cable pulsating loads.
Outdoor lighting collects snow and wind waves the whole etc. This is taken into account, in particular at the ends of the wires in the fastenings of the structures. Furthermore, taking into account the wire shackles number of connection points. At least two wire shackles, and taking account the effect of the corrosion to wire. A simple design includes a number of things to consider, so that the designer can sleep with peace of mind the night.
The calculation of human fatigue, the steel girder bending and many things are synonymous. If the girder is placed on top of a larger load => increases the deflection of the girder. If a man is set to bear a greater burden => increases the spent performance time. The used time has the same meaning in terms of fatigue, because fatigue increases time. The athlete's fatigue level may partially determine by the basis of the time. On the other hand, if the girder length is increased while maintaining the same load => growing even in this case the deflection of the girder. In human cases the increasing distance => increases execution time (used time). These things are clear concepts, without counting the associated same meanings.
Time comparisons, it is often a one-dimensionality. Interestingly, the road running time consists of the time arised through all dimensionalities (up and down - left and right - time (dilation). The wire movement is forward and back, the pulleys conveying the movement through the dimensionalities. Rigid steel bar in place of the service; does not own the thread-like property of matter. Thread (wire) and its design is not essential, but the lack of reference to the thread moment (torque). The matching situation arises in connection with running, where the missing moment does not preclude different dimensionalities. This is calculated, the physics and physiology having the same notes. This will be discussed soon in the form of calculation. (306)
54. WEIGHT OF STEEL PLATE
The plate thickness as the merchantable quality is equivalent to calculation. The shape of a plate variates, such the vessel bottom in the pictures and the main girder of the crane. Plate needs designer, which produces technical drawings. Designer has items, which define the quality and thickness of the material.
Physicist asks, what is the specific gravity of the steel plate and draws a circle with calipers. He says the diameter of the circle to be one (1) unit. The plate thickness is also one (1) unit. Steel gravity of this by calculating is 0.785. You may determine the quantities up to you, because the relativity does not matter of them.
3,14.. x 12 x 1 = 0.785
4

Infrmation of the plate thickness and quality transmits to the parts list. By way of proportionality, these values transmits through parts to end product.
Values are proportional also when different sized product, but having comparable function. We will come to calculate tasks of this. The products in the images are of demanding steel structures.

Thickness of the Plates
The plate thickness can calculate, and there is no need remember them. The plate thicknes was the first thing, of which I understood the issues of proportionality.
0,6 - 0,8 - 1 - 1,2 - 1,5 - 2 - 2,5 - 3 - 4 - 5 - 6 - 8 - 10 - 12 - 15/16 - 20 - 25
0,63 - 0,8 -1 - 1,2 - 1,6 - 2 - 2,5 - 3,15 - 4 - 5 - 6 - 8 - 10 - 12 - 16 - 20 - 25
1,25 x 0,8 = 1 1,25 x 16 = 20
Steelworks make plates having factor 1,25. When plate thickness 0,8 mm, it is same do we have 0,75 mm or 0,8 mm thickness of plate. The same of plate thickness 15 and 16 mm. The weight of steel plate is three-dimensional, in which variables are thickness, width and length. In practise the weight is easy to define by a pocket calculator.
As a Thumb Rule: One square meter of 1 mm steel plate = 8 kg
Steel plates are being made on + thickness tolerance. From steel specific gravity 7,85 we transfer through + tolerance to the relative value 7,85 x 1,03 = 8,0. This is general way defining the steel plate weight. The weight is according to the surface area and plate thickness. When the surface area stay the same and thickness changes, factor 1,25 is being raised to indicated potency. Proportionality in steel plate is clearly noticeable. Of this kind calculation did I first practise to shape the proportionality. (878)
1. 2. 3. 4. 5. 6. 7.
1 - 1.25 - 1.6 - 2.0 - 2.5 - 3.15 - 4 - 5 - 6.3 -8.0 - 10
Example 1: Plate PL 5 3150 x 2500 mm => 8 kg/m2 x 3.15 m x 2.5 m x 5 = 315 kg
1.255 = 3.15 m 1,254 = 2,5 m
8 kg x 5 (1.255 x 1.03) x (1.254 x 1.03)= 316 kg
8 kg x 5 x 1.259 x 1.032 = 316 kg ( exact weight )
1,257 = 5 (plate thickness)
.
8 kg x 1.257 x 1.03 x 1.259 x 1.032 = 311 kg
8 x 1.2516 x 1.033 = 311 kg (differs 1,6 % )
Now the question; what is the factor 1,03?


55. ROUND BARS STOCK ITEM SET
Let us drawn up on the basis of the strength a logical set of round bar stock items. This can be obtained by combining the Fibonacci and ratio numbers by a factor of 1.25. When the diameter of the steel bar increases by a factor of 1.25 (general machine construction fatigue factor), the cross-sectional areas follow the Fibonacci numbers.
Fibonacci numbers ( 1 ) - 1 - 2 - 3 - 5 - 8 - 13 - 21 - 34 - 55
Ratio numbers (D cm) (1)- 1.2(5) - 1.6 - 2 - 2.5 - 3,2 - 4 - 5 - 6,3 - 8
A round bar cm2 0,785 1 2 3,15 4,91 8,04 12,57 19,63 33,18 51
1. 2. 3. 4. 5. (6.).
The proportionality limit is five steps, where the accuracy stays.
The Diameter series for machine construction
10 - 12 - 16 - 20 - 25 - 32 - 40 - 50 - 65 - 80 - 100.... mm
An Example:
Round bar diameter 8 cm => A = (3,14... x D2) / 4
A = (3,14... x 82) 4
A = 50,27 cm2
Fibonacci numbers round bar diameter 55, has a cross sectional area of 50.27 cm2. Steel cross-section diameters have a + tolerance, in which case the value of 50.25 cm2 may be increased by the value of 51 or lowered by value of 50 cm2. The calculation of this does not matter, when the steel rod cross-section is increased by a factor of 1.25 (in machine-building the general fatigue factor), then the cross-section surface areas follow the Fibonacci numbers.
Golden Ratio
The ratio number increases two steps, increases the diameter by a factor of 1.6(18).
Step 1 Step 2
Esim. D 2.0 cm - D 3.15 cm 3.15/2 = 1.6(18)
D 4,0 cm - D 6.3 cm 6.3 / 4 = 1.6(18)
D 6.3 cm - D 10.0 cm 10 /6.3 = 1.6(18)
The cross-sectional surface area increases by a factor of 1.6(18)2
Step 1 Step 2
D2.0 cm - 3.15 cm2 - 33.18 cm2 8,04 / 3.15 = 1.6(18)2
D4.0 cm - 12.57 cm2 - 33.18 cm2 33,18 / 12.57 = 1.6(18)2
The EP-calculation is not calculation of decimal places.
Static Values
D cm 1 - 1.2(5) - 1.5(1.6) - 2 - 2.5 - 3.2 - 4 - 5 - 6.3 - 8 - 10
Ix cm4 0.0491 0.12 0.32 0.785 1.92 5.15 12.56 30.7 77.3 201 490.1
Wx cm3 0.0981 0.192 0.40 0.785 1.53 3.21 6.28 12.3 24,5 50.3 98.2
(+2) (+1.6) (+1.25) (1) (-1.25) (-1.6) (-2) (-2.5) (-3.15) (-4) (-5)
Wx / Ix Ix / Wx
a) Free fall of a body 4,91 m /1 sec
b) The gravity force 9.81 m/s2
c) The specific gravity of steel 0.785
d) Calculation factors 1.25 and 1.12
e) The full angle 2 x pi radians (6.28)
f) Fibonacci numbers 1 - 1 - 2
1 + 1 = 2
D10 0,0491 Ix cm4 - 0,0981 Wx cm3 etc.
0.0491 cm4 + 0.0491 cm4 = 0.0982 cm4
D10 0.0981 Wx cm3 - D12(.5) 0.192 Wx cm3
The shown set covers the cross-sections on the basis of strength. The selected set features will be presented in the strength calculation.
56. GENERAL OF MEASURING
 Also big makers fail sometimes when measuring axles and associated parts. A domestic knowledge and noteworthy company delivered a device to a customer. Also big makers fail sometimes when measuring axles and associated parts. A domestic knowledge and noteworthy company delivered a device to a customer.
According to company's strength calculator, there was an axle which measurement excitement was of largeness 2,5 kN/cm2. Any on the basis of the calculated point, axle not should have been broken. In any way, this happened. Were as the reason some swinging loads on the axle, the axle's fiberlike material in key-way position or which points led for damaging in the axle? The calculation shows one possibility of a failure.
The car manufacturer launched to the market a new product, which drive shafts lasted under 100 000 km, can be said in each car. Drive shafts paid about 600 euros a piece as installed. The factory promised meet in all 100,000 km and under driven car, paying an other and the customer other installation. Although car development had lasted many years, still stayed told lapsus in the product. In some cars, also glued doors unfastened the outside sheet panel from internal frame part.
In failing of the big maker, do we know about expectable problems? This presentation being acquainting to the Equivalent Proportional Calculation, must remember the calculation offers only frames to the measurement. Each product when final measurements, should be ensured countable with the traditional manner as has taught. We will come to observe the small difference between these two calculation. Later when the Equivalent Proportional Calculation has stabilized, can to its resources leave more and more. At first is however reason to compare calculation between and observe which properties get moved by way of the Equivalent Proportional Calculation. (547)
57. NORMAL STRESS CALCULATION
Well-known force acts over an area. The amount of normal stress is the active force divided by the surface area. The larger the surface area, the smaller the stress. This is enough at first, which is later to be completed by Equivalent Proportional Calculation. (860)
Click on the image
58. BENDING CASE 1 CALCULATION
The most necessary information for the strength calculating is the body bending under load. Of the load cases one of the most common is the general case in which the concentrated load effects in the middle of the girder which is supported at the both ends. Deflection consists of the concentrated force in the middle and of the girder own weight. The calculation takes into account both deflections. The calculation to HEB100 - HEB500 profiles. (695)

f = F x L3 / (48 x I x E)
L1000 σt Ix Wx Iy Wy Area
Profile cm kN/cm2 cm4 cm3 cm4 cm3 kg/m A cm2
HEB100 518 2,2 450 90 167 33,5 20,4 26
Deflection of the girder weight;
F = Girder weight
5.18 m x 20.4 m/kg = 1.04 kN (105.6 kg)
L = from table 518 cm
Ix = from table 450 cm4
E = constant 20600 kN/cm2
f = deflection
f = 5 x F x L3 / 384 x E x I
f = 0.204 cm
Deflection of the concentrated force;
F = 1 kN
f = F x L3 / 48 x I x E
f = 0,314 cm
Total deflection;
0,204 cm + 0,314 cm = 0,518 cm
518 cm / 1000 = 0,518 cm
1:1000
59. PASCAL'S TRIANGLE FACTOR 11
In mathematics, Pascal's triangle row factor between the lines is 11, but in EPC calculation the ratio is 1.1 and the following shows the value of the coefficient of 11.
Pascal's triangle
1 dim 1 = 1 1 = 1
2 dim 1 1 = 1 +1 = 2 1.1 x 1 = 1.1
3 dim 1 2 1 1.1 x 1.1 = 1.21
4 dim 1 3 3 1 = 8 1.1 x 1.21 = 1.331
5 dim 1 4 6 4 1 1.1 x 1.31 = 1.4641
The factor of the fourth dimensionality is 1.331


Deflection
When the load grows twice bigger the total change grows 11 times bigger. The distance of the deflection grows eight times bigger when twice longer span. The same shows the row of the 4 dim.
That cannot see is the Universal Friction; 1.331 x 8 x 1.03(28) = 11
Time dilation table
The growth of the span has the character of one-dimensionality, with a factor of 1.25. Just as the spacecraft travels in the space 75,000 km/s and this resulting the time dilation "friction" coefficient 1.03(28). It can be noted from the table. With the progress of a three-dimensional world, the fourth dimensionality brings its own factor.
1.253 x 1.03 = 2
Time dilation of moving particles

Profile L1000 σt Ix Wx Iy Wy Area
Nimike cm kN/cm2 cm4 cm3 cm4 cm3 kg/m A cm2
HEB100 518 2.2 450 90 167 33.5 20.4 26
Table: When span of 519 (518) cm => deflection 0.518 cm
Deflection of the Girder Weight;
The girder weight
10.36 m x 20.4 kg/m = 2,08 kN
f = Deflection
f = 5 x F x L3 / 384 x E x I
f = 3.279 cm
Deflection of the Concentrated Force;
F = 1 kN
f = F x L3 / 48 x I x E
f = 2.499 cm
Total Deflection;
3.279 cm + 3.251 cm = 5.800 cm
5.800 cm / 518 cm = 11.2
1 - 1.12 -1.25
11.2
112
(factor 1.12)
Calculation is not decimal placing. (898)
60. GOLDEN TRIANGLE
In the triangle the lengths of the margins are 1 and 0.5 unit => hypotenuse is 1.1(18) units and perimeter 2.618 units. The Golden Ratio is square root of 2,618 and means 1.618 x 1.618 = 2.618. In the phenomenon, when studying the alteration of value. The known value has its proportional value 1 => the one dimensional (1d) change is 1.118 (1.12). The value alteration is 1.4641 times as the Pascal's Triangle shows.
Image above lefft: 1 / 1.618 = 0.618 Golden ratio 1.618
Image below on the left: 1 - 1.12 - 1.25 Ratio sequence
Image below on the right: 2 x 0.5 + 0.618 Golden ratio 1.618
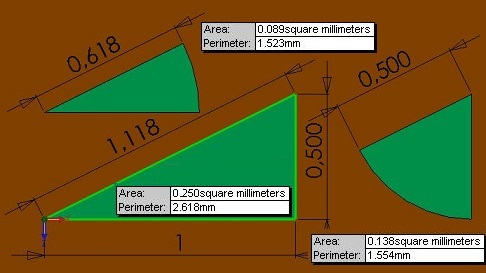
0,618 + 0,500 = 1,118
0,618 / 0,500 = 1,236
1 + (2 x 0,118) = 1,236
1 / 1,618 = 0,618
0,138 / 0,089 = 1,55
1,2362 = 1,527
1,618 x 1,618 = 2,618
1 + 1,618 = 2,618
 The girder is loaded and the length of the span increases 1,1(18) times the original length. Deflection increases 1,46 times the original deflection. The girder is loaded and the length of the span increases 1,1(18) times the original length. Deflection increases 1,46 times the original deflection.
We calculate something what is the whole and something what is not. The whole is the triangle and its area of 0,25 units, the factor 1.25 of the ratio numbers.
The value (1.118) that is not the whole, consists of two sector values (0.618 + 0.5). There are no units, because we calculate universal mathemathics.
In addition to an invisible, there is the universal friction of 1.03 (1,25 => 1,03 in the table).
It is good to remember that the whole is not decimals.
0,089 + 0.138 = 0,227
Sector 1 + sector 2 = 0.227
0,25 / 0,227 = 1,1
The whole / part wholes = 1.1
The lost part of the whole is Pascal's Triangle and its row factor 1.1.
0.1 1
0.2 1 1 1,1 x 1,0 = 1,1
0.4 1 2 1 1,1 x 1,1 = 1,21
0.8 1 3 3 1 1,1 x 1,21 = 1,33
1.6 1 4 6 4 1 1,1 x 1,331 = 1,46
1 6 1 1 6 1 1,1 x 1,4641 = 1,61
Together = 6,71 ( x 10 -11 )
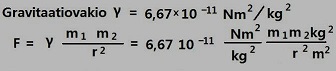
.
Finally the Pascals triangle formulates the Gravitational Constant. This is an example how the areas of phi geometry are the same as the calculation. Gravitation is still unresolved, in which a few decimal difference is not significant. (954)
61. AXIAL DEFORMATION
Axial compressive strain of steel bars will tell you how much length is shortened, or conversely, it will stretch when squeezed or pulled. Power is 1 unit, cross-section 5 units and length 100 units. => Relationship between axial compressive strength and the range is 1 / 1000. This relationship existing, others are known without formula. Take a few minutes to think about this. Gravitation is 9.82 m/s2. Calculation uses generally cm unit. The calculation is based on the Newton - Gravitation - Surface Area - Figure Five combination. One feature of the calculation is the Visual Geometry, which means the figures and calculations are visually shaping the reality. The calculation image above is a calculation that represents the accession of each other names. At this point, is enough to detect the ratio of the links between them. Eventually, surface area and strength are the same meaning. Axial compression rod is inversely elongation rod. The calculation uses the value 20600 cm4 of the Modulus of Elasticity.
This is easy to remember
F = 1 kN L = 100 cm A = 5 cm2 ό = 0,001 E = 20 600 kN / cm4
Basic load is always 1 kN
Length 100 cm is easy to remenber
Deformation 0,001 cm
Beam cm
F kN ==> ==================== <== kN
ό = 100 cm x 1 kN x cm2 = 0,001 cm
20600 kN x 5 cm2
Kaava laskee teräksen puristuman ja venymän, tarvitsematta ymmärtää laskelmaa. Suhdelaskenta tarvitsee lähtöarvon, jota kaava ei vaadi.
The formula calculates steel deformation and elongation, without need to understand the calculation. EPC calculation requires an output value, which is the formula does not require.
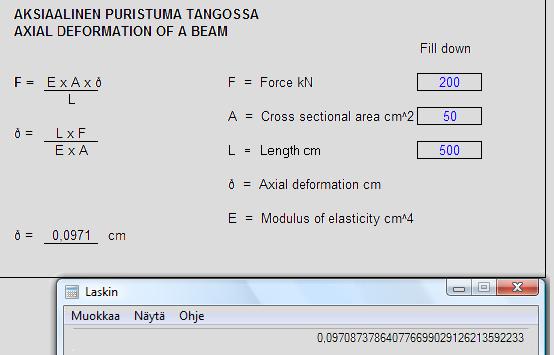 Click on the calculation Click on the calculation
EPC Calculation
Example 1
F = 200 kN => FΔ = 200 (x 1 kN)
L = 500 cm => LΔ = 5 (x 100 cm)
A = 50 cm2 => AΔ = 10 (x 5 cm2)
ό = 0,001 x FΔ x LΔ = 0,001 x 200 x 5 = 0,09708
1,03 x AΔ 1,03 x 10
Example 2
F = 1200 kN L = 800 cm A = 315 cm2 ό = ?
ό = 0,001 x FΔ x LΔ = 0,001 x 1200 x 8 = 0,1479
1,03 x AΔ 1,03 x 63
(Spread sheet calculation gives 0,1479)
Example 3
F = 0,3 kN L = 20 cm A = 1 cm2 ό = ?
ό = 0,001 x FΔ x LΔ = 0,001 x 0,3 x 0,2 = 0,000291
1,03 x AΔ 1,03 x 0,2
(Spread sheet calculation gives 0,0003) (919)
62. SPACE DIAGONAL IN THE STRENGTH OF MATERIALS
In the strength calculation the normal stress having the nominal value of 1 ==> the shear sress of the same power has the value of 1.7 according to formulas. The strength calculation ables know the before said.
The normal stress having the nominal value of 1 (edge length of the cube) ==> the shear stress of the same power has the value of 1.7 according to formulas. The strength calculation ables know the before wrote.

SQR = Square root
SQR (3) = 1.7
The figure above maintaining one decimal made the same. Both values (1.118 and 0.618) are of two different hypotenuses, such as cutting and bending are from different points in bended beam. The shear stress effect difference between the forces is 1.70 times the nominal value of 1.
1.1(18) + 0.6(18) = 1.7
Therefore, firewood cutting is done with an ax, not trying to pull the wood to pieces.
70. CALCULATION EXAMPLES
Example 1
HEB200 profile has the load of its own weight. Span of 1 meter (100 cm) grows five times by a factor 1.1, so the new span will be 161.051 cm. The calculated deflection by the program and having ten decimals accuracy is 0.6675226738 cm. Set the deflection of the span 161.051 cm.
Profile L1000 σt Ix Wx Iy Wy
cm kN/cm2 cm4 cm3 cm4 cm3 kg/m A cm2
HEB200 1062 2 5700 570 2000 200 61.3 78.1

f = 5 x F x L3 / (384 x E x I)
f = 5 x 9.694722627 kN x 1610.513 cm3 / (384 x 20600 kN x cm x 5700 cm4)
f = 4.4907861 cm
Unfortunately, the pocket calculator was able to nine decimal place. Often one decimal accuracy is sufficient for practical calculation tasks, but the example is in order to prove the accuracy of the EP-calculation.
a) EP-Calculation
As input data the profile 100 cm bends 0.6675226738 cm. EP-calculation does not need the table, so the information of HEB200 profile and static values are redundant.
Deflection 161,051 cm
Initial data x Changen = New deflection
0.667526738 cm x Changen = 4.4907861 cm
Accuracy is in this seven decimals, but ten decimal precision is included in the calculation. A more detailed presentation of the calculation is shown on my pages, if you read them.
b) EP-Calculation
If you are familiar with gravitational constant in physics, and read it have written on these pages. You calculate the task in the following way.
6.72561 x 0.667526738 cm = 4.49 cm, having the sufficient accuracy
Example 2
Engineers need the static values in order to be able to calculate simple things. If you tell them of the profile deflection 0.10828 cm of its own weight. They understand the amount of a deflection. Then asking how much the profile bends when the span is 16.051 m, you will not receive any answer. In their view, the output data are insufficient to the task. Strange?
Therefore, there is the EP-calculation which does not require the tables to calculate. The constant of gravitation is constant and, as a result deflections is constant. Further, it leads to the speed of light and time dilation and the geometric shape is well known in mathematics. Therefore, calculate the previous example, and take any cross-section, which you measure the increase in the above ratio. From this we can move on to other relationships, but do not confuse them for this.
You may well count yourself in this example.
Example 3
8.77565 m long steelprofile has set between two supporters in accordance with Example 1. The measured deflection of its own weight is 0.17112049 cm. Set the deflection to four decimal places, if the length of steel profile is 17.84991 m
f = fo x time dilationn
f = 0.17112049 cm x time dilationn
f = 2.9290729618768053382408109555241 cm
After some efforts, the calculated deflection of the program would be 2.929072981 cm. In addition, there is no measuring device that could separate these two methods result. The above refers to EP-calculation to be able for more precise calculations (having three decimal places) than some calculators have decimals or measuring device accuracy.
In addition, the calculated item does not have to be a really exist as a profile, a tabled curve or a product manufactured, so that its characteristics were known. In this EP-calculation is different from the other calculation never before shown.
Just ask this task of your professor or teacher. I guarantee they will not be able to answer. They should not be able to give the question, because I'm the only one capable to this answer. Soon we all can it.
The units of measurement for EP-calculating are irrelevant. Equally, it may have dimensions of inches, feet or whatever.
Example 4
HEB200 profile has the load of its own weight. Span grows twice (2 x ) longer, the new span will be a - b - c - d times the initial deflection?. Static values table and calculation formula are shown below. The task is to determine deflection of the formula. Why is this happening?
Profile L1000 σt Ix Wx Iy Wy
cm kN/cm2 cm4 cm3 cm4 cm3 kg/m A cm2
HEB200 1062 2 5700 570 2000 200 61.3 78.1

f = 5 x F x L3 / (384 x E x I)
Answer options
a b c d
4 12 16 20 - times the initial deflection
The only variable in the formula is L, from which you can deduce the answer. Can you even then, in which you find out by calculating the formula values.
21.6 2018*08:00
www.karikolehmainen.com
Epcalculation@gmail.com
|