Fysiologian toiset perusteet
1. Viisikulmaisuuden jatkumo
2. Fysiologia ja sen suhteellisuus
3. Viisi elementtiä
4. Ihmisen keho
4.1 Ihmisen pituus
4.2 Navan sijainti
4.3 Kyynärpään sijainti ihmisillä.
4.4 Ihmisen pään korkeuden ja leveyden suhde.
5. Ihmiskehon mittasuhteet
6. Käden mitat käsineestä
7. Ihmisen painon muodostuminen
...................
17. Painoindeksi.
1 8. Luonnollinen kävelyvauhti
18.1 Fysikaalinen heiluri
18.2 Kävelyvauhti
1 9. Energiankulutus ylipainoisella
20. Taipuminen yleisesti
.......................
31. Fysiologinen taipuma.
32. Vaijerin puuttuva momentti
33. Ihmisen ikä suorituskykynä
34. Cooperin testitaulukko miehet.
35. Kilpaa juokseminen
36. Tuotteistettu kilpaurheilu.
37. Juoksulajien tarkastelu
38. Aikavertailut urheilussa
39. Juoksutapahtuman varjo
40. Fibonaccin lukujono, 200 m ME
50. Aika neljäs ulotteisuus
51. Kuulantyöntö tosiasia
52. Pituushyppy ennätykset
53. Bob Beamonin pituushypyn laskenta
54. Todennäköisyys samasta syntymäpäivästä.
55. Pyramidiharjoittelu
1. Viisikulmaisuuden jatkumo
Meritähdet (Asteroidea) ovat piikkinahkaisiin kuuluvia merten selkärangattomia. Niiden ruumiinmuoto muistuttaa tähteä, jossa yleensä on viisi sakaraa, tai viidellä jaollinen määrä. Niillä ei ole aivoja, eikä päätä. Historiallisesti meritähdet ovat ensimmäisten joukossa syntyneitä, josta muoto tässä yhteydessä on merkillepantava.
Laajimmin hyväksytyn teorian mukaan nykyihmiset kehittyivät Afrikan savanneilla noin 200 000–250 000 vuotta sitten. Ihmisellä on aivot ja kehittyneet raajat, joiden avulla se voi käsitellä työkaluja kätevämmin kuin mikään muu eläinlaji. (671)
Leonardo da Vinci - Vitriviuksen mies
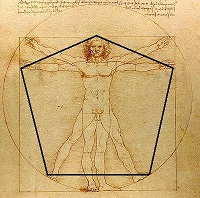
"Mitä enemmän asiat muuttuvat, sen saman kaltaisempina ne pysyvät."
Ambrose Swasey -professuurin hoitaja Lawrence Krauss, Case Western Reserve University
2. Fysiologia ja sen suhteellisuus
Samaa tarkoittavan suhdelaskennan materia, fysiikka ja fysiologia ovat samaa tarkoittavaa, lainalaisuusuuksien juontuessa alkuräjähdykseen. Nykykäsityksen mukaan esimerkiksi aikaa ei ole ennen alkuräjähdystä.
Laskennassa esitetään vertailuja aikana maailmanennätysten syntymisestä ajassa taakse- ja eteenpäin. Teemme näitä ennätysten tarkasteluja kansallisten tulosten (Suomessa) perusteella, kuin maailmanlaajuisena ennätysten tarkasteluna.
Tarkastelemme Berliinin ME-tuloksia ja tämän jälkeen ME-tuloksia Pekingin olympialaisissa. Molemmissa kisoissa syntyi 100 ja 200 m ME-aika miesten juoksumatkoilla. Kuinka tulokset muuttavat laskentaa tai muuttavatko ne sitä mitenkään? Asioita ja paljon, niiden liittyessä tarkasteluihin fysiologian otsikon alla. Tärkeätä on havaita teräksen taipuman ja urheilijan väsymisen olevan samaa tarkoittavaa sekä esitettävää laskemalla ja kuvioina. Näin näkemisen geometria osoittautuu samaa tarkoittavaksi edellisten kanssa.
3. Viisi elementtiä
Vesi - Puu - Tuli - Maa - Metalli
Käännetään joskus muodossa viisi vaihetta, viisi ainetta, viisi liikettä, viisi askelta/askelmaa. Kiinalaisessa maailmankatsomuksessa ja filosofiassa viidellä elementillä on keskeinen osa. Kiinalaisen maailmankatsomuksen mukaisesti asiat syntyivät energian (gin) kulkiessa viiden vaiheen läpi. Tämä on vanha maailmankatsomus, jolla ei ole länsimaista vastinetta. Viisi elementtiä ovat energian siirtymistä paikasta tai olomuodosta toiseen. Energiaa ei voi tuhota ja maailmankaikkeuden energiatasapaino on välttämätön osa tapahtumia eri muodossaan. Vertaa tätä kaavaan E = m c2.
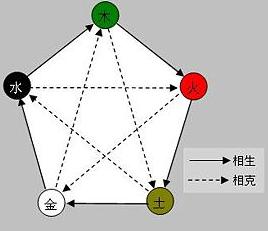 Viiden elementin teoria ulottuu esihistorialliselle ajalle. Pienenä havaintona, teoria on alkujaan kirjoitetussa muodossa oraakkelikirjoituksena.
- Kuvio on kiinalaisilla n. 6 000 vuotta sitten.
- Pythagoras käyttää kuviota neljätuhatta vuotta myöhemmin.
- Samaa tarkoittava suhdelaskenta käyttää kuviota kuusituhatta vuotta myöhemmin.
Kuva Wikipedia
Laskennan ajatus on kaiken olevan selitettävissä kaavalla E = m c2. Energiakupla, joka puhkeaa ja muodostaa maailman. Tämän selityksen antavat, tällä hetkellä parhaiten asiaa tuntevat tiedemiehet. Kiinalaisen ajattelun mukaan kaikki maailman ilmiöt voitiin jakaa viiteen elementtiin. Tulemme kiinalaiseen astrologiaan, joka on monelle länsimaalaiselle tuttua. Kaukoidän kansojen keskuudessa viisi elementtiä ovat keskeinen osa ajattelua. Elämän kulkua määrittävät kuvatut viisi elementtiä niin pukeutumisessa, syömisessä, taistelulajeissa, lääketieteessä, astronomiassa, ajanlaskussa, rakentamisessa, hautajaisissa kuin uskonnollisissa menoissa.
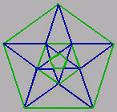 Tuhansia vuosia myöhemmmin, voi havaita vastaavuuden Pythagoraan ajattelusta viisikulmion kautta, jota hän piti jumalallisena kuviona. Oletuksena hän sain tiedon viisikulmiosta käydessään Egyptissä, missä tapasi egyptiläisiä oppineita. Kuvio esittää kultaisen leikkauksen suhdeluvun 1,618 muodostumisen, laskennan osoittamalla tavalla.
Thousands of years later, can detect the equivalence of the Pythagorean way of thinking through the pentagon, which he regarded as a divine pattern. By default, he was informed of pentagon, on his visit to Egypt, where he met with the Egyptian scholars. Pentagon presents the golden section ratio of 1.618 as the calculation shows. (505)
4. Ihmisen keho
4.1 Ihmisen pituus
Erilaisista kuvioista ja numeroista on sanottu, ettei niistä ole löydettävissä todellisuuteen liittyvää. Samoin sanotaan numero viidestä liittyen viisikulmioon, joita molempia Pythagoras piti pyhänä lukuna ja kuviona.
Suhdelaskennan idea on, ettei laskettavaa tarvitse välttämättä nähdä. Esimerkiksi luurangon pituus on 175,4 cm, jolloin halutaan tietää, millä korkeudella napa on ollut henkilön eläessä. Mitan saa skaalaamalla alimmaisen kuvion piirtämisohjelmalla tai laskemalla sen ylemmän esimerkin mukaisesti.
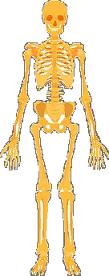
Luurangon pituus pituus 175,4 cm on tunnettu tieto, josta tuntematon navan sijainti kantapäästä mitattuna on;
175,4 cm / 1,618 cm = 108 cm
Tuntemalla navan sijainnin, ihmisen pituus on;
108 cm x 1,618 cm = 174,5 cm
Kannamme kultaisen leikkauksen lukusuhdetta 1.618
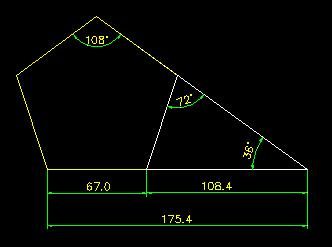
Skaalaamalla kuvion, saa halutun mitan selville.
Laskenta tällä sivulla on EP-fysiologiaa, mutta myös näkemisen geometriaa. Kaikilla eläimillä ovat vastaavat mittasuhteet, kuten ihmisillä on. Ei ainoastaan eläimillä, sillä kuolleet koneenelimetkin sisältävät samat mittasuhteet.
4.2 Navan sijainti
Navan sijaintia mitatessa on hyvä ajatella, missä napa sijaitsee normaalipainoisella, jos se roikkuu vatsan päällä matkalla maata kohti. Myös normaalipainoisissa on ruumiinrakenteen poikkeavuuksia, joten mikään eksaktia mittaa ei edellisten esimerkkien mukaan voi määrittää navan paikalle. Luonto muutenkin on täynnä poikkeavuutta, vaikka suuressa mittakaavassa noudattaakin luonnon käsikirjaa, jonka samaa tarkoittava suhdelaskenta kuvaa laskemalla. Laskemme suhteellisuutta alle 5 % tarkkuudella. Esimerkiksi 180 cm pitkän henkilön navan sijainti voi siten poiketa joitakin senttimetrejä lasketusta. On olemassa henkilöitä, joilla on suhteettoman pitkät jalat ja toisaalta lyhyet. Kummatkaan poikkeavat mitat eivät ole optimaalisia ja sen voi joissakin tapauksissa päätellä kävelemisestä.
Leonardo da Vinci
Leonardo da Vinci tutki ihmisen mittasuhteita ja monet hänen taulunsa ovat tässä mittasuhteessa.
Leonardo da Vinci - Vitriviuksen mies
Marcus Vitruvius Pollio oli roomalainen 1. vuosisadalla eaa. elänyt kirjailija, arkkitehti ja insinööri. (1083)
4.3 Kyynärpään sijainti ihmisillä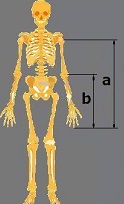
Ihmisen vartalossa napa ei ole ainoa kehon osa, joka toteuttaa mittasuhteen Fii (1,618). Mittaamme käsivarren pituuden ja tarkastamme kyynärpään sijainnin.
Mikäli käsivarren pituus on 71 cm, käsivarren pituus sormenpäästä kyynärpäähän on 44 cm.
71 cm / 1,618 = 44 cm
Suhdelaskenta antaa suhteelle luonnollisen lujuuteen perustuvan selityksen. (1081)
4.4 Pään korkeuden ja leveyden suhde
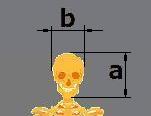
Mittaa pääsi leveys ja korkeus, jolloin saat todennäköisen mittasuhteen a / b = 1,6.
- Pää ja muut vartalonosat tulevat kuvatuksi oikeassa suhteessa
- Lujuudella on maailmankaikkeuden mittasuhde
- Kauneus on sopusuhtaisena mittasuhteena piirustuksessa
Kultainen leikkaus on kaikkialla läsnä
(726)
5. Ihmiskehon mittasuhteet
Leonardo da Vinci aavisti lukuun 1,618 liittyvän suuremman, josta viestitti tuleville sukupolville monella tavalla.
Laskenta tutustuttaa Leonardo da Vincin tutkimukseen ihmiskehosta. Tällöin Vitriviuksen mies ja suhdeluku 1,618 tulevat tutuiksi. Ihmiskehon mittasuhteet mahdollistaa globaalin vaatteiden valmistamisen miljardeille ihmisille kaikkialla maapallolla. Vaatteiden valmistus on ajatukseltaan samaa tarkoittavaa suhdelaskennan kanssa. Tuntemalla arvon tuotteesta, tunnet suurella todennäköisyydellä muut arvot vastaavista tuotteista. Ihmisen voi ajatella varioivista mitoista, asian olematta näin. Käymme esimerkkeinä, kuinka suhteet muodostuvat ihmisissä ja laitteissa. Entäpä materiaalit, poikkeammeko koneista?
Yksikköympyrä (d= 1) pinta-alana on 0,785 yksikköä
- kyse on pinta-alasta
12 * 3,14 / 4 = 0,785
Raudan ominaispaino on 0,787
- Paino ja paine pinta-alaa kohti.
Keskiarvo luvuista
(0,785 + 0,787) / 2 = 0,786
0,7862* 1,618 = 0,618 x 1,618 = 1
Arvo 1 vastaa ihmisen pituutta, jolloin navan sijainnin saa kertoimella 1,618. Samaa tarkoittavasti raudan ominaispaino, yksikköympyrän pinta-ala ja napa ovat määritettävissä kertoimella 1,618 nimellisestä arvosta 1. Lujuus ja voima materiassa on määritettävissä tiedon perusteella myöhemmin esitettävällä tavalla. Fysiologia ihmisessä on samaa tarkoittavaa raudan eli teräksen käyttäytymisen kanssa. Tämä on kiistämätön laskennan esittämä todellisuus. (36)
6. Käden mitat käsineestä
Suhdelaskennan periaate on, ettei tutkittavaa tarvitse nähdä, mikäli tämä on heittänyt varjon. Varjon tutkiminen riittää tiedon saamiseksi kohteesta. Siksi seuraava esimerkki on laskennan periaatteen esittämiseksi, kuin kyse käsineestä. Tosin miehen talvikäsineen mittasuhteet selviävät samalla. Tehtäessä suurempi tai pienempi käsine. mittasuhteet säilyvät silloinkin.
Leonardo da Vince tutki ihmisen mittasuhteita, todettuaan kultaisen leikkauksen suhdeluvun 1,618 kautta olevan mahdollista määrittää ihmisen mittasuhteita. Tiedon avulla on valmistettavissa maailmanlaajuisesti vaatetusteollisuuden tuotteita. Vaatteista voi tämän jälkeen siirtyä muihin tuotteisiin ja niissä esiintyvien mittasuhteiden tarkastelemiseen,
 Kuvassa on käteen tyköistuva talvikäsine, josta näkee peukalon ja pikkusormen välin olevan 21 cm. Sormikas vastaa käden muotoa tasoon levitettynä. Etusormen päältä pikkusormen päälle mitta on:
21 cm / 1,618 = 13 cm
Käden leveys
13 cm / 1,618 = 8 cm
Käsineen leveys kuvassa on 10 cm. Käden leveys saadaan kertoimella 1,25.
10 cm / 1,25 = 8 cm
Käsineen pituus
1,1 x 21 = n. 23 - 24 cm.
7. Ihmisen painon muodostuminen
100 kg ( 1 kN) painavan ihmisen paino muodostuu; Happea 65 kg, hiiltä 18 kg, vetyä 10 kg, typpeä 3 kg, kalkkia 2 kg ja fosforia 1 kg. Puuttuva 1 kg sisältää rautaa, tinaa, jopa kultaa ja hopeaa häviävän pienen määrän. Lisäksi 25 alkuainetta. kalium, rikki, kloori, natrium, sinkki, magnesium, mangaani, kupari, koboltti, molybdeeni, nikkeli, alumiini, kromi, titaani, pii, rubidium, litium, arseeni, fluori, bromi, jodi, seleeni, boori, barium ja strontium.
Materiaalien käyttö ohjautuu samanlaisten fysikaalisten lainalaisuuksien alaisena ihmisen kehossa, kuin koneen rakenteessa. Taivutus, puristus, veto, nurjahdus, kiepahdus, voitelu, jäähdytys jne.
Hengityksen mukana saamme happea ja typpeä, typen palautuessa käyttämättömänä.
Veren hemoglobiini sisältää rautaa. Raudanpuute tunnetaan puutostilana.
Ravintomme muodostuu hiiliyhdisteistä, jolloin meissä on hiiltä.
Vetyä meissä on vedessä hapen ja typen yhdisteessä.
Ruskea tukka => kuparia, cobolttia ja rautaa.
Harmaa ja valkoinen tukka => paljon nikkeliä.
Tina => ei tunneta
Vaaleatukkaisuus => luultavasti titaanista.
Molybdeeni => tukan punainen väri.
Kehomme, se mitä näemme itsessämme rakentuvat protoneista ja neutroneista, koostuen 13,7 miljardia vuotta sitten syntyneistä kvarkeista. Samassa muodostui laskennan matemaattinen lainalaisuus. Fyysinen keho näin kuvattuna, muistuttaa alkuaineiden osalta koneen materiaalikuvausta. Tulemme mistä koneet tulevat, sillä valmistamiseksi tarvittavat mineraalit saadaan maasta.
Hopeavesi
Eräs erityisvalmiste on hopeavesi, jota käytetään tulehdusperäisten sairauksien hoitoon ja ennaltaehkäisyyn. Hopeavesi toimii viruksia, bakteereita ja sieniä vastaan. Tuotteen valmistusta Suomessa valvoo Kuopion Yliopiston kemian laitos. Elintarvikkeet sisältävät hopeaa mm. jauhot 0,3 ppm, leseet jopa 1 ppm, maito 25...30 ppm, liha 40 ppm ja kalassa jopa 10 ppm.
Ihmisessä hopeaa on 9 mg keskimäärin 50-vuotiaalla henkilöllä. Se sijaitsee luissa, ihossa, hiuksissa ja pehmytkudoksissa. Veressä hopeaa on n. 3 ppm ja pehmytkudokisssa 10...250 ppm. Erään kaupallisesti myydyn hopeaveden pitoisuus oli 30 ppm per 100 ml.
Hopean vaikutuksen tunsivat myös lännen raivaajasukupolvet. Lähtiessään matkalleen yli preerioiden, oli vankureissa vesitynnyri. Vesitynnyriin pudotettiin hopeadollari, joka piti veden kauemmin juomakelpoisena. (37)
17. Painoindeksi
Monet asiat ovat suhteellista. Aikuinen on ylipainoinen, kun kehon rasvapitoisuus ylittää tietyn suhteellisen rajan, painoindeksin. Painoindeksi kg/m2 lasketaan paino jaettuna pituuden neliöllä, toisin sanoen pituuden peitolla (fysiikassa vastaava valon nopeus c2). Kyseessä on paine, kuten jännitysten tai vaikkapa energiakaavassa E = m c2. Massan (m) yksikkö painoindeksissä on kg. Normaali painoindeksi on välillä 19 - 25. Tässä ei selvitetä poikkeuksia indeksin laskentaan.
Painoindeksi = massa kg / pituus2 m
Painoindeksi = m / l2
E = m c2
1 - 1,25 - 1,6 - 2
18,5...24,8 - 25...29,9 - 30...34,9 - 35...40
Normaali paino - lievä ylipaino - merkittävä ylipaino- vaikea ylipaino
18,5 x 1,25 / 1,03 = 22,45
22,45 x 1,25 /1,03 = 27,2
27,2 x 1,25 /1,03 = 33
33 x 1,25 /1,03 = 40
Suhdelaskennassa valon nopeus ja painoindeksin pituus muodostavat pinta-alan. Toisin sanoen peiton paineen laskemiseksi. 1,03 on kaikkialla esiintyvä staattisen väsymisen kitka.
L = 1,77 m Kg = 85 => 85 kg / 1,772 m = 27,1 kg /m2
_____________________________________________________
18,5 x 1,25 / 1,03 = 22,45
22,45 x 1,25 /1,03 = 27,2
27,2 x 1,25 /1,03 = 33
33 x 1,25 /1,03 = 40
L = 1,77 m Kg = 85 => 85 kg / 1,772 m = 27,1 kg /m2
18. Luonnollinen kävelyvauhti
Kaikilla eläimillä on niiden luonnollinen kävelyvauhti, ihminen tähän mukaan lukien. Yksi jalan heilahduksen jakso, on täysi edestakainen heilahdus. Jos jalan pituus on 98 cm. Paljonko aikaa kuluu jalan heilahduksen liikkeeseen (askelpariin = S = 2 x 75 cm)? Askeleen pituus 75 cm on mitattu kävellessä tai ne voivat olla maahan jääneitä jälkiä. Näin dinosaurusten kävelynopeuden voi määrittää jälkikäteen. Eikä ainoastaan dinosaurusten kävelynopeuden. Ymmärrämme matkan ja nopeuden liittyvän ajan käsitteeseen. Pituus on määritettävää yksinkertaisella mittanauhalla ja etäisyys käyttäen jotakin yksikköä kuten maili tai kilometri. Laskemalla pääsemme syvemmälle ajan käsitteeseen, kuin kelloa tarkastemalla. Tuotteilla ovat samat lainalaisuudet aikaan, kuin kaikilla muillakin
Preferred walking speed
18.1 Fysikaalinen heiluri
T = 2 x Pi x NJR (2 L / 3 g) NJR = neliöjuuri
T = 2 x Pi x NJR (2 x 0,98 / 3 x 9,8)
T = 1,62 sec Kultainen leikkaus 1,618
T = Aika s g = 9,8 m/s2 L = 0,98 m Pi = 3,14...
18.2 Kävelyvauhti
v = S / T
v = 1,50 m / 1,62 sec = 0,80 m/s = 3,3 km/h
v = Nopeus m/s S = Yhden jakson pituus
Moni sanoo kävelevän kuusi kilometriä tunnissa. Kenties hetken, mutta ei kauan. Tämä, sillä on olemassa suhteellisuus jalan pituuden ja painovoiman kesken. (747)
19. Energiankulutus ylipainoisella
Obesity a research journal; January 2012
Energetic Cost and Preferred Speed of Walking in Obese vs. Normal Weight Women
Testaamalla tutkittiin oletusta, jonka mukaan ylipainoisen energiankulutus kasvaa ja he suosivat alhaisempaa kävelynopeutta. Tutkimukseen osallistui 20 vapaaehtoista, joista 10 normaali- ja 10 ylipainoista naista. Kävelynopeudet olivat 0,50 - 0,75 - 1,0 - 1,25 - 1,5 ja 1,75 m/s. Viisi minuuttia kävelyä ja tämän jälkeen viiden minuutin tauot. Energiankulutus kasvoi 11 %, joka vastaa Pascalin kolmion rivikerrointa 1,1. Tuloksena ylipainoiset kävelivät samalla nopeudella kuin normaalipainoiset 1,40 - 1,47 m/s eli 5,0 - 5,3 km/h.
1,0 - 1,12 - 1,25 - 1,6
1,11 x 100 % = 111 %
1 1
1 1 1,1 x 1 = 1,1
1 2 1 1,1 x 1,11 = 1,21
1 3 3 1 1,1 x 1,21 = 1,331
Suurin nopeus testissä oli 1,75 m/s = 6,3 km/h. Puolet kävelyn ajasta oli lepoaikaa. Tämän seurauksena nopeudeksi jäi korkeimmillaan 3,15 km/h. Tämä vastaa ihmisen luonnollinen kävelyvauhti esimerkkiä, jossa Kävelijä jalan pituudella 98 cm, kävelee luonnollista nopeutta n. 3,3 km tunnissa.
20. Taipuminen yleisesti
Fysiikkaa ja fysiologiaa ymmärtämättä, ei ymmärrä taipuman olemusta. Se on vaikeaa, sillä fysiikka ei opeta taipumaa. Taipuman katsotaan liittyvän lujuuden määrittämiseen, joka kuuluu insinöörikoulutukseen. Silti, taipuma liittyy teoreettisiin oppiaineisiin, kuten se liittyy tunnetuinpaan energian kaavaan. Energian kaavojen kautta on selitettävissä myös urheiluun liittyviä kysymyksiä. Fysiologinen taipuma lisää suorituksen aikaa, jonka voi osoittaa aikadilaationa.
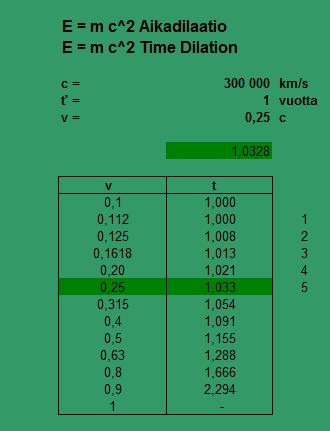
Yksinkertaistaen, kappaleen taipuma aiheuttaa venymän ja kutistumisen, jonka ulkoinen ilmentymä on kappaleen muodonmuutos. Tästä sanotaan kappaleen taipuvan. Fysiologian yhteydessä aika taipuu, toisin sanoen kasvaa suorituksen mukana aikadilaationa. (678)
31. Fysiologinen taipuma
Taipumasuhde 1:1000 on taipuman määrittämisen lähtöarvo. Fysiologiassa viitataan tähän arvoon, sillä taipuma ja väsyminen ovat samaa tarkoittavaa. Kaiken minkä luette sivuiltani, liittyy ennemmin tai myöhemmin toisiinsa. 1:1000 taipumasuhde on väsymisen varjo monessa merkityksessä. Seuraava taulukko esittää pojasta mieheksi - miehenä olemisen - miehestä vanhaksi (ei vanhukseksi) kuvauksen kuntona.
Cooperin testin tulokset miehet
Ikä Erinomainen Hyvä Keskitaso
1,06 1,1 1,21
13–14 > 2700 m 2455 m 2231 m Kunto paranee
15–16 >2862 m 2602 m 2365 m
17–20 >3034 m 2758 m 2507 m Paras kunto
20–29 >2862 m 2602 m 2365 m
30–39 >2700 m 2455 m 2231 m Kunto huononee
40–49 >2547 m 2315 m 2105 m
50-60 >2403 m 2185 m 1985 m
Ikä
(13-14) - (15 - 16) - (17 - 20) - (20 - 29) - (30 - 39) - (40 -49) - (50 +)
12.5 - 16 - 20 - 25 - 32 - 40 - 50
13 x 1.25 = 16
16 x 1.25 = 20
20 x 1.25 = 25
25 x 1.25 = 32
32 x 1.25 = 40
40 x 1.25 = 50
Edellä oleva on esimerkki elävästä materiasta taulukoituna tietona.Tämä on niin sanottua varmaa tietoa. Ihminen tuotteena kuntona liittyy tietoon.
Seuraava esimerkki on kuolleesta materiasta, kuten HEB I-profiilit. Tämä on myös varmaa tietoa. Kaikissa profiileissa on kuormitettuna taipumasuhde 1:1000.
Nimike cm kN/cm2 cm4 cm3 cm4 cm3 kg/m A cm2
HEB100 518 2.2 450 90 167 33,5 20,4 26
HEB120 644 2.1 864 144 318 52,9 26,7 34
HEB160 868 2 2490 311 889 111 42,6 54,3
HEB200 1062 2 5700 570 2000 200 61,3 78,1
HEB240 1235 2 11260 938 3920 327 83,2 106
HEB320 1534 2.1 30820 1930 9240 616 127 161
518 x 1.25 = 647
647 x 1.25 = 808
808 x 1.25 = 1010
1010 x 1.25 = 1262
1262 x 1.25 = 1577
Loppupäätelmä
Elävä materia antaa energiansa liikkeessä, jolloin aika vastaa taipumaa. Mitä kauemmin jokin suoritus kestää, sitä enemmän taipumista. Kun kuollut materia teräs taipuu kuormitettuna 1:1000 taipumasuhteessa, jännityksen arvo on kaikissa poikkileikkauksissa sama. Kerroin 1,25 liittyy kumpaankin ja tästä syystä nimitys samaa tarkoittava suhdelaskenta. Ihminen (elävä) ja silta (kuollut) ovat molemmat tuotteita ja niillä on yhteinen peruste kuntona ja kantavuutena. Mitattava jännevälin pituus ja ihmisen ikä ovat lopulta samaa tarkoittavaa, kun ne suhteutetaan toisiinsa.
32. Vaijerin puuttuva momentti
Ohut lanka asetetaan kahden pisteen välille, joita kuvaavat pisteet A ja B. Langan voi olettaa olevan kevyen, jolloin tukivoimat A ja B ovat pienet.
A = B = G / 2
 Jotta kevyt lanka ei riipu, sitä pitää vetää kokoonsa nähden äärettömän suurella voimalla. Langan lujuuden tulee tästä syystä olla äärettömän suuri, jotta lanka kestää vedosta aiheutuvan voiman. Tätä tilannetta ei oikeassa elämässä synny. Vastaavan kaltainen tilanne silti syntyy sähkövoimalinjoissa, joissa langat riippuvat. Ohuisiin lankoihin syntyy vetojännitys, mutta ei taivuttavaa momenttia. Langasta puuttuvan jäykkyyden seurauksena, langan mitoitus perustuu poikkileikkauksen pinta-alaan.
Poikkileikkauksessa jossa on pieni taivutusvastus, syntyy käytännössä vetojännitys. Vaijerilla ja sähkölangalla on huono kannatuskyky, puhumattakaan työntämisestä, mutta suuri vetokyky. Veto muodostaa vetojännityksen, jolloin lanka on varsin yksinkertainen mitoittaa. Kappaleilla, jolla on jäykkyys => syntyy veto- ja puristusjännitys, jotka ovat erimerkkiset poikkileikkauksen vastakkaisilla puolilla. Keskellä on neutraaliakseli, jossa jännityksen suuruus on nolla.
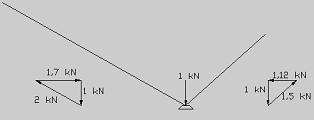 Ripustettaessa valaisin epäkeskeisesti ajoradan yläpuolelle, syntyy kuvan kuormitustapaus. Suunnittelijan suunnittelun ohjelma tekee vaijereiden voimien määrittämisen yksinkertaiseksi. Tämän jälkeen määritetään riittävä varmuus vaijerin tykyttävälle kuormitukselle. Ulkona sijaitseva valaisin kerää lunta ja tuuli heiluttaa kokonaisuutta jne. Tämä huomioidaan erityisesti lankojen päissä olevissa kiinnityksissä rakenteisiin. Edelleen huomioidaan vaijerisakkeleiden määrä kiinnityskohdissa. Vähintään kaksi vaijerilukkoa, sekä huomioidaan korroosion vaikutus lankaan. Yksinkertainenkin mitoitus sisältää useita huomioitavia asioita, jotta suunnittelija voi nukkua rauhallisin mielin yönsä.
Laskennan kannalta ihmisen väsyminen, teräskannattajan taipuminen ja monet asiat ovat samaa tarkoittavia. Jos kannattajan päälle asetetaan suurempi kuorma => lisääntyy kannattajan taipuma. Jos ihmisen kannettavaksi asetetaan suurempi taakka => kasvaa suoritukseen käytetty aika. Aika on samaa tarkoittavaa väsymisen kannalta, sillä väsyminen lisää aikaa. Urheilijan väsymisen tason voi osittain määrittää käytetyn ajan perusteella. Toisaalta jos kannattajan pituus kasvaa kuormituksen säilyessä samana => lisääntyy tässäkin tapauksessa kannattajan taipuma. Ihmisen tapauksessa etäisyyden kasvaessa => kasvaa suoritukseen käytettävä aika. Nämä asiat ovat selviä käsitteitä, laskematta niihin liittyvää samaa tarkoittavuuksia.
Aikavertailuissa kyse on usein 1-ulotteisuudesta. Mielenkiintoisesti maantiejuoksussa aika muodostuu kaikkien ulotteisuuksien kautta (ylös - alas - sivuille - aika(dilaatio). Vaijerin liike on edestakaista etenemää, köysipyörien välittäessä liikkeen eri ulotteisuuksien kautta kulkevaksi. Terästanko jäykkänä ja paikallaan olevana, ei omaa langan kaltaista materian ominaisuutta. Lanka ja sen mitoitus eivät ole oleellista, vaan viittaus langan puuttuvasta (vääntö)momentista. Vastaavuus syntyy juoksemisen yhteydessä, jossa ns. puuttuva momentti ei estä eri ulotteisuuksia. Tämä on laskettavaa, jolloin fysiikka ja fysiologia toteavat saman. Tähän palataan laskennan muodossa. (306)
33. Ihmisen ikä suorituskykynä
 Tarkastelussa eri-ikäisten ihmisten kunto määritetään laskennallisella tavalla. Laskennan tuloksen varmistuessa satoina miljoonina suorituskertoina, joka takaa luotettavan vertailupohjan, taulukon osoittamana tilastotietona.
Ajattelemme olevamme yksilöitä, joiden kesken ei ole mahdollisuutta vertailemiseen. Ihmisen suorituskyky juoksemalla on 1-ulotteista etenemistä. Vertailu on mahdollista tehdä taulukosta ja voi myös itse tehdä testauksen kunnon määrittämiseksi. Homo Sapiens tieto löytyy internetistä. Kuten aina asioiden yhteydessä, myös nyt tulee ymmärtää määrättyjä asioita, jotta tutkimus olisi mahdollinen.
Hakusana; Homo Sapiens suoritusteho, ei anna vastausta, Kysymällä samaa sanalla Cooper-testi, asia muuttuu toiseksi.
Riittääkö sadan miljoonan tai miljardin juostun juoksun tulos? Vuonna 1968 Kenneth H. Cooper kehitti USA:n armeijalle 12 minuutin Cooper-testin. Testi antaa karkean arvion juoksijan kunnosta. Lopputulokseen vaikuttaa luonnollisesti juoksijan motivaatio suorituksen aikana ja vaatii harjoittelua. Ilman harjoittelua 12 minuutin arvioiminen on vaikeaa ja johtaa helposti suureen vauhtiin, joka kostautuu.
Ensin tulostetaan Cooper-testin tulokset. Havaitaan tulosten olevan jaetun ikäryhmiin ja neljään kuntoluokkaan. Testaamisen kannalta 13-vuoden ikä on alhaisin ikä, josta on saatavissa luotettava testitulos. Armeija ei hyödy alle tämän iän tuloksista, joten aineisto nuoremmista ikäluokista on urheiluseuroilla. Aiemmin lähes kaikki kykenivät testin juoksuun, mutta tänä päivänä kaikki eivät siihen kykene eri syistä. Testi tässä mielessä esittää juoksemaan kykenevien tuloksen. Tuotteesta ihminen, tämä ei kerro kaikkea, vain tiedon siihen osallistuneista. (359)
34. Cooperin testitaulukko miehet
Testi on laadittu USA:n puolustusvoimien tarkoitukseen. Sen laati Kenneth H. Cooper vuonna 1968. Se soveltuu hyvin suurten massojen suorituskyvyn tarkasteluun.
Testissä juostaan mahdollisimman pitkä matka 12 minuutin aikana.
Vakiotestinä, tämä tulee suorittaa vakio-olosuhteissa:
Lämpötila 10 - 25°C, ilman kosteus enintään 75 % maksimista
Vakio 400 m tartan rata tai vastaava
Testattavalla ei saa olla hengitysvaikeuksia.
Taulukon matkat metrejä.
Ikä Erinomainen Hyvä Keskitaso Huono Hyvin huono
13–14 2700+ 2400 – 2700 2200 – 2399 2100 – 2199 m 2100-
15–16 2800+ 2500 – 2800 2300 – 2499 2200 – 2299 m 2200-
17–20 3000+ 2700 – 3000 2500 – 2699 2300 – 2499 m 2300-
20–29 2800+ 2400 – 2800 2200 – 2399 1600 – 2199 m 1600-
30–39 2700+ 2300 – 2700 1900 – 2299 1500 – 1899 m 1500-
40–49 2500+ 2100 – 2500 1700 – 2099 1400 – 1699 m 1400-
50+ 2400+ 2000 – 2400 1600 – 1999 1300 – 1599 m 1300-
Taulukon mukaan 20-vuotias mies on parhaassa kunnossa. Neljäkymmentävuotias mies on suurinpiirtein saman kuntoinen kuin neljätoistavuotias poika. Myöhemmin laskemme taulukon, joka perustuu suhdelaskennan kertoimiin 1,06 - 1,12 ja 1,25. (741)
35. Kilpaa juokseminen
Kautta aikojen on juostu kilpaa. Aina antiikin ajoista voittajan on määrittänyt juoksijan suhteellinen asema maalissa. Edellä oleva voittaa takana tulevan. Vertailukelpoinen ajan määrittäminen on vain muutamia kymmeniä vuosia vanha asia. Ennen suhdelaskentaa ei ole ajan määrittämistä laskemalla.
Istuessa stadionin katsomossa näkee edessään juoksuradat.
100 ja 200 m juoksut tapahtuvat suoralla radan osuudella, mutta 400 m juoksu tapahtuu ovaalin muotoisella radalla. Pidät tätä luonnollisena, sillä et pysty seuraamaan 400 m juoksua, jos se juostaisiin suoralla radalla. Ymmärrät paljon luonnon ilmiöiden muodostumisesta. Ilmiöiden laskentakaavat näyttävät aluksi etenevän suoraviivaisesti, kuten juoksuradat valokuvassa, mutta saavat käyrän muodon, kuten juoksuradat. Juoksutapahtuman laskentana voi tästä johtuen liittää muihin ilmiöihin. Fibonaccin lukujono kertoo lyhyet juostavat matkat, hahmottamalla ensin lyhyin matka 100 m yhden yksikön pituiseksi.
1 - 1 - 2 -
100 m + 100 m + 200 m
36. Tuotteistettu kilpaurheilu
Kilpaurheilu on tuotteistettu, siinä laskennan poikkeamatta käytännössä teknisistä tuotteista. Laskenta huomioi energian käytön matkan aikana, samoin energian tuoton henkilön kokoon ja painoon suhteutettuna. Laskemme myös energian käytön ihmisen ikäryhmien kunnon mukaiseksi, jolloin ihmisen koolla ei ole merkitystä. Cooperin-testi ei kysy painoa tai pituutta, vain ikää. Laskenta tuottaa yllätyksen ihmisen koon suhteen ja lihasten tehontuottoon urheilijoiden kesken. Kultainen leikkaus on tässä mukana. Voimme laskea energiana juoksumatkan, saada se aikana ikäluokalle, matkalle, kuntoryhmälle jne. Laskenta ei sisällä vilppiä mutuna uskottavaksi. Laskin kädessä päättelette johdonmukaisesti urheilun tilan. Kun yksi edellisiin liittyvistä tunnetaan, muukin on tunnettua. Kenties ette halua saada sitä selville?
Kunto on energian tuottoa, käytännössä hapenottokykykyä. Laskemme esimerkiksi juoksuasennon vaikutusta suoritukseen, vertaamalla tämä siltanosturin pääkannattajaksi. Paljonko energiaa sitoutuu taipumaan, sillä taipumisesta on kysymys huonossa juoksuasennossa ja tämän kuluttaessa energiaa.
Siltanosturin pääkannattaja ei nostossa taivu kuorman voimasta. Sen tekee vaikkapa vesivoimalan potentiaalienergiasta muunnettu sähkö, joka nostaa kuorman pääkannattajan päälle sijoitettuna nostokoneistona. Kyse on potentiaalienergiasta, joka siirtyy kimmoenergiaksi pääkannattajaan. Puhumme puristus ja vetojännityksestä näkemällä sen silmin taipumana. Emme ole laskeneet, mihin energia menee, kuinka paljon ja miksi. Rautalangan taivuttamisen käsissä tiedämme, laskematta paljonko lanka tuottaa energiaa. Lujuuslaskennassa jännitysten laskemiseen rakenteessa, käytetään usein paljon aikaa, tekemällä tämä muodonmuutosten tarkastelun kustannuksella.
Lopuksi ajatellaan metallin epäkeskopuristinta, joka taivuttaa kappaleen. Iskun kesto on sekunnin murto-osia ja taivuttamiseen tarvittu energia suurelta osin siirtyi lämmöksi taivutettuun kappaleeseen. Jäljelle jää fyysinen muoto kappaleesta, jossa jäähtymisen jälkeen on sama energian määrä, kuin ennen muodon muokkausta. Juoksijakin lopulta tuottaa vain lämpöä. Asioita voi tarkastella yksinkertaisesti, ottamalla asian kerrallaan. Laskemisessa on usein kyse parhaista tuloksista, joten maailmanennätyksiin on hyvä tutustua. (657)
ME-tilastoja
37. Juoksulajien tarkastelu
 Esimerkiksi olympiakisoissa juostavia matkoja ovat 100, 200, 400, 800 ja 1500 m juoksut. Neljä ensimmäistä matkaa yhteen laskemalla on 1500 m.
Brittiläisessä kansainyhteisössä juostaan mailin matkaa 1609 m, joka arvona on kultaisen leikkauksen suhdeluku 1,618. Laskemalla yhteen 1500 m + 800 m + 400 m + 200 m + 100 m = 3 000m. 1500 m ja 1609 m matkan yhteen laskemalla, on pituus 3109 m, joka vastaa piin arvoa 3,14.
Juostava 3000 m matka, on matemaattisen rakentamisen palikkana yhteenliityvä, vaikkapa teräsprofiileihin HEB 100, HEB 160, HEB 200 ja HEB 300 kanssa, jotka liittyvät lujuuslaskentaana. Teräsprofiilin poikkileikkausta korkeutena ja juoksumatkan pituutta voi aluksi miettiä ajatuksen tasolla samaan pohjautuviksi.
100 m 200 m
400 m 800 m 1500 / 1609 m
- Lyhyet juoksumatkat => ovat matemaattisesti laskettavia suorituksia.
- Yhteenlaskettu pituus matkoille on piin (3,14) arvo.
- Hahmottamalla, rakennuspalikat ovat keskenään suhteessa ja laskettavaa.
- Lopulta teräskannattajan taipuman ja juoksusuorituksen voi laskea ristiin. ME-aika 800 m juoksussa on jotakin, jolloin teräskannattaja taipuu samoin. Myös maratonin juoksun aika määräytyy laskemalla. Näkemisen geometria esittää nämä käyrinä, josta havaitsee yhtenevät käyrät. (10)
38. Aikavertailut urheilussa
Lontoon olympialaiset olivat tätä kirjoitettaessa. Sanotaan, ettei Pascalin kolmiossa ole mielenkiintoista, eikä siihen kannata uhrata aikaa. Uskommeko tähän? Kuviona kiinalaiset tunsivat Pascalin kolmion tuhansia vuosia sitten. Tänään havaitsemme, kuvion vastaavan juostavia matkoja. Kiinalaisilla ei ollut ajanoton välinettä, mutta olemme varmoja heidän kilpailleen ainakin eläimillä. Tänään kilpailemme mitä moninaisemmilla tavoilla ja osaamme suhteuttaa suorituksen toiseen vastaavaan suoritukseen. Lontoossa rikkoutui entinen 800 m maailmanennätys. Tästä me kirjoitamme, sillä tiedämme ajan olevan nopeimman koskaan saavutetun. Se mitä emme tiedä on, onko uusi maailmanennätys ali- tai ylivertainen muihin matkoihin nähden. Tätä voi vertailla Pascalin kolmion kautta.
Lontoon olympialaiset ovat tätä kirjoitettaessa vuonna 2012. Sanotaan, ettei Pascalin kolmiossa ole mielenkiintoista, eikä siihen kannata uhrata huomiota. Uskommeko tämän? Kuviona kiinalaiset tunsivat Pascalin kolmion tuhansia vuosia sitten. Nyt havaitaan, kuvion vastaavan juostavia matkoja. Muinaisilla kiinalaisilla ei ollut ajanottoon välinettä, mutta olemme varmoja heidän kilpailleen ainakin eläimillä. Tänään kilpailemme mitä moninaisemmilla tavoilla ja osaamme suhteuttaa suorituksen ajan toiseen vastaavaan suoritukseen. Lontoossa rikkoutui 800 m juoksun maailmanennätys. Tästä kirjoitetaan, sillä tiedetään ajan olevan nopeimman koskaan saavutetun. Se mitä emme tiedä on, onko uusi maailmanennätys ali- tai ylivertainen muihin matkoihin nähden. Tätä voi vertailla Pascalin kolmion kautta.. (421)
39. Juoksutapahtuman varjo
Matematiikka on kuin talon rakentamista tiilistä. Rakennelma valmistuu tiili kerrallaan, joka on sama asia myös fysiologian yhteydessä. Osaat rakentaa talon, osaat ajatella rakennelman, joka tarvitaan suorituksen yhteydessä. Lyhin sadan metrin juoksumatka on tiili, joita latomalla muut matkat rakentuvat. Yksinkertaista kuin heinänteko, kuten joskus asia ilmaistaan. Jotta voi luoda uutta, on ajateltava uudella yksinkertaisella tavalla kuten E = m c c, joka sisältää kaiken. Hyvä on, rakensin pyramidin joka loppujen lopuksi sisältää paljon enemmän kuin uskallamme ajatella.
100 100 m
100 100 200 m
100 200 100 400 m
100 300 300 100 800 m
100 400 600 400 100 1600 m
1600 m (maili 1609 m) juoksumatka on nykyään mieluummin 1500 m
Pisin juoksumatka - lyhin juoksumatka
1600 m - 100 m = 1500 m
Pascalin kolmio määrittää ratajuoksun viisi lyhyintä juoksumatkaa eli viisi suhteellista matkaa ilmiöllisessä avaruudessa. Pascalin kolmio on kaksiulotteinen kuvio, jota kolmeulotteisuudessa vastaa pyramidi.
40. Fibonaccin lukujono, 200 m ME
Fibonaccin lukujono alkaa 1 - 1 - 2... Pascalin kolmion alkaessa saman kaltaisesti.
100 m - 100 m - 200 m
Pascal's Triangle
Yleisurheilun 100 m juoksu
100 m 9,58 sec
100 m + 100 m 9,58 sec + 9,58 sec
100 m juoksun ME-aika on 9,58 s. Tunnettuna tietona.
200 m ME
2 x 9,58 sec = 19,16 s (ME 19,19 s)
Laskelman tarkkuus on 0,156 % ME-aikaan 19,19 s nähden. Myöhemmin laskemme pieniä ja suuria asioita keskimääräisellä 2 % tarkkuudella. Vielä ei yleisesti tunneta tuotteiden muodostumista ja fysiologista käyttäytymistä asioissa, näiden tullessa päivä päivältä selitetyksi. Laskenta on luotu tuotteisiin, siirtyen tästä fysiologiaan ja fysiikkaan. (302)
50. Aika neljäs ulotteisuus
Ulotteisuudet
1-ulotteisuus liike etenevänä, kuten juoksu eteenpäin
2-ulotteisuus pinta-ala käsitteen kautta, voima ja vahvuus
3-ulotteisuus tilavuus
4-ulotteisuus aika, kuten Hermann Minkowski sen ymmärsi
Hermann Minkowski
Opiskelu Sveitsissä sujui Albert Einsteiniltä kohtalaisesti. Hermann Minkowskin matematiikan luennot Einstein laisti, uskoen ettei myöhemmin tarvitsisi korkeampaa matematiikkaa. Tätä hän jälkeenpäin katui.
Kun Albert Einstein algebrallisesti esitteli erityisen suhteellisuusteorian vuonna 1905, Hermann Minkowski osoitti entiselle oppilaalleen, että sen voi ymmärtää myös geometrisesti teoriana neliulotteisesta aika-avaruudesta. Myöhemmin Albert Einstein havaitsi, että geometrinen näkemys avaruusaikaan olisi tarpeen täydentämään omaa myöhempää työtä yleisenä suhteellisuusteoriana (1915). Suhteellisuuden kannalta huomattavaa on Albert Einsteinin esittäneen saman algebrallisesti, jonka Hermann Minkowski esitti geometrisesti.
Laskennan ajatus on, kuten yllä mainitussa tekstissä. Ilmiöitä voidaan tarkastella mittaamalla, laskea ja esittää geometrisesti. Kuinka laskemme kahdensadan metrin juoksun maailmanennätyksen. Tätä fysiikka ei laske?
Esimerkki yksiulotteisuudesta - Lyhyet juoksumatkat
Kuvio esittää juostavien matkojen noudattavan Pascalin kolmiota.
1 1 1 x 100 m = 100 m
2 1 1 2 x 100 m = 200 m
4 1 2 1 4 x 100 m = 400 m
8 1 3 3 1 8 x 100 m = 800 m
16 1 4 6 4 1 16 x 100 m = 1600 m (maili)
Tämä on näkemisen geometriaa nähdä lyhyet juoksumatkat
Fibonacci numerot
1 - 1 - 2 - 3 - 5 - 8 - 13 - 21 - 34 - 55 - ....
Fibonaccin lukujono alkaa 1 - 1 - 2... Pascalin kolmio alkaa saman kaltaisesti.
100 m + 100 m = 200 m
Yleisurheilun 100 m juoksu
100 m juoksun ME-aika on 9,58 s.
200 m ME - 200 m WR
2 x 9,58 sec = 19,16 s (ME 19,19 s)
100 m + 100 m = 200 m
1 - 1 - 2
Juostessa ensimmäinen 100 metriä, tapahtuu matkalla väsymistä. Toivon teidän tietävän, ettei maailmassa ole juoksijaa, joka pystyy täysillä juoksemaan sata metriä. Ilman väsymistä aika olisi oletettavasti seuraavan laskelman mukainen.
9,58 s / 1,0328 = 9,276 s.
200 metrin matkalla, kun väsyminen huomioidaan
2 x 9,276 x 1,0328 = 19,16 s
ME -tuuliolosuhteet
100 m: Tuuli + 0,9 m/s 200 m: Tuuli - 0,3 m/s
Esimerkiksi tuuli tekee eron aikaan 19,16 s = 19,19 s. Ymmärrätte, että tämä on ainoa tapa laskea tämän kaltaisia ilmiöitä kuten juoksutapahtumat. Aikadilaation kautta laskenta muodostuu osaksi fysiikkaa. Molemmat maailmanennätykset ovat Usain Boltin nimissä, joka tekee ajoista vertailtavaa. (412)
51. Kuulantyöntö tosiasia
Kuulantyönnön tarkoitus on työntää painava kuula mahdollisimman pitkälle. Lajissa välineurheilu ei näyttele suurta osaa. Tarkastelemalla maailmanennätyksiä, saamme kuvan, kuinka ihmisen fysiologia kehittyy ja kuinka nopeasti. Joskus yleisen käsityksen mukaan, tämän päivän urheilutulokset ovat harjoitttelussa niitä, joita parhaimmillaan saatiin aikaan vuosikymmeniä sitten. Tällä hetkellä voimassa oleva kuuulantyönnön maailmanennätys on vuodelta 1990. Nyt miesten ennätyksestä on kulunut 24 ja naisten 27 vuotta.
Randy Barnes 23,12 m 20.05 1990 Westwood, CA
Natalja Lisovskaja 22,63 m 7.6 1987 Moskova
Ennätykset Suomessa?
Reijo Ståhlberg 21,69 5.5 1979
Asta Ovaska 18,57 20.8 1989
Suomessa miesten ennätyksestä on kulunut 35 vuotta. Mika Halvari työnsi 22,09 m vuonna 2000, jota sisähallin vuoksi ei hyväksytty. Johtopäätöksenä kuulantyönnön ennätys ei rikkoudu helposti. Miesten kuulantyönnön SE taso vuonna 2014, on 60-luvun ME taso. Tulemme samaa tarkoittavuuteen, jolloin tulokset ovat vuosikymmeniä verrattavia keskenään. (644)
52. Pituushyppy ennätykset
Ihmisen fysiologian määrittämät ennätykset säilyvät kauan, jonka todistaa tilastotieto tuloksista. Aloitamme pituushypyllä. Tiedämme urheilijoiden voiman ja nopeuden kasvaneen huimasti 90-luvulla verrattuna 60-luvun tuloksiin. Onko näin, sen tilasto osoittaa alla olevan mukaisesti.
8,95 m Mike Powell Tokio 30.08 1991 Tokyo
8,90 m Bob Beamon Meksiko 18.10 1968 Mexico
8,31 m Greg Rutherford Lontoo 04.08 2012 London
Bob Beamon hyppäsi 8,90 m Meksikossa vuonna 1968. Kului 23 vuotta ja ennätys parantuu 5 cm. Tällä hetkellä aikaa on kulunut 21 vuotta edellisestä ennätyksestä. Rutherfordin voittotulos 831 senttiä on heikoin voittotulos olympialaisissa sitten vuoden 1972.
Long jump
8,22 m Tommi Evilä Göteborg 26.06 2008 Sweden
8,16 m Rainer Stenius Los Angeles 06.05 1966 USA
Suomen ennätys parani 6 cm 42 vuoden jälkeen. Olemmeko saavuttaneet maailman ennätystä vai jääneet jälkeen? Jesse Owens hyppäsi 8,13 m 25.05 1935 ja Ralph Boston 8,24 m 27.05 1961. Edellä oleva tarkoittaa suomalaisten olevan jäljessä 50 vuotta, huomioitaessa tämän hetken ennätys 8,22 m. Millainen käsitys meillä on ihmisen fysiologian kehittymisestä? Suhdelaskenta tuo ajateltavaa ihmisten kehittymisestä monessa mielessä. (643)
53. Bob Beamonin pituushypyn laskenta
Tiedot
a) Kilpailija voi aloittaa hyppynsä mistä tahansa pisteestä rajaviivan takaa;kuitenkin mitattu etäisyys on aina kohtisuorassa rajaviivasta lähimpään jonkin kehon osan jättämään jälkeen hiekassa.
b) Bob Beamon hyppäsi tuloksen 8,90 m. Hän työskenteli hänen nopeutensa parantamiseksi tekniikkaa, jossa hyppääjä ei niinkään hyppää kuin kävelee ilmassa ". Parhaat hyppääjät ovat usein olleet pikajuoksijoita. Hänen vauhdinottonsa kesti kuusi sekuntia ja hypyn pituus oli tuloksena lähtönopeudesta 9,5 m/s.
c) "Meksikon ohut ilmanala vaikutti hypyn pituuteen, 2250 metriä meren pinnan yläpuolella.
d) Tuuliolosuhteet olivat täydelliset Beamonin ennätyshyppyyn, +2 metriä sekunnissa. Suurin hyväksyttävä tuulen nopeus on kaksi metriä sekunnissa (m/s).
e) Painovoiman kiihtyvyys Mexico City 9.766 m/s2
f) Pituus 1,91 m. Paino 70 kg
Hypyn lentorata
Oletetaan hyppääjän olevan elävä aseen kuula. Aseen suurin kantama saavutetaan suuntaamalla piippu 45 asteen kulmaan maan pinnasta. Ase on kiinteästi paikallaan sillä ammuttaessa, mutta hyppääjä on vaakasuuntaisessa liikkeessä. Maailmanluokan hyppääjät jättävät maanpinnan kahdenkymmenen tai sen alle olevassa hyppy kulmassa. On fysiikan lakien vastaista sanoa hypyn laudalla suuntautuvan noin 20 asteen kulmaan, joten oletetaan sen olevan 45 astetta. Ilmassa hyppy hyvinkin suuntautuu kahdenkymmenen asteen kulmaan, jossa on yhtenä osatekijänä vaakasuora liike-energia. Hyppääminen kulmaan ja kulman näkeminen silmin, ovat kaksi eri asiaa, joten tätä on syytä tarkastella.
Hyppääjä ei niinkään hyppää, vaan vipuaa itsensä laudalla 45 asteen kulmassa eteenpäin, joka näyttää kahdeltakymmeneltä asteelta. Hyppääjä vipuaa itsensä laudalla 45 asteen kulmassa eteenpäin, joka ilmalennossa näyttää noin kahdeltakymmeneltä asteelta.
Ensimmäinen tapa määrittää hypyn pituus
Hyppylaudalla vaakasuuntainen hyppynopeus on 9,5 m/s / neliöjuuri (2) = 6,718 m/s
Pysty- ja vaakasuora komponentti kumpikin 6,718 m/s
Pascalin kolmio näkemisen geometrian mukaan
1 dim 1 m
2 dim 1 1 m2
3 dim 1 2 1 m3
4 dim 1 3 3 1 s
6,718 m/s x 1,331 s = 8,94 m (ME 8,90 m)
Toinen tapa määrittää hypyn pituus
Bob Beamonin hyppy Mexico City 1968
Aikadilaatio taulukko
9.5 m/s / 1,03282 = 8,90 m
Pascalin kolmio näkemisen geometrian mukaan
1 dim 1 m 1,0328
2 dim 1 1 m2 1,03282
3 dim 1 2 1 m3 1,03283
4 dim 1 3 3 1 s
Hypyssä on vaaka- ja pystysuora komponentti eli pinta-alaa.
Kolmas tapa määrittää hypyn pituus
Hypyssä on kaksi samansuuruista nopeuskomponenttia. Vaakasuora 6,72 m/s ja 45 asteen kulmassa oleva pystysuuntainen nopeuskomponentti. Näiden komponenttien resultantti on puolet 45 asteesta eli 22,5 astetta. Tämä on kulma, jossa hyppääjä näyttää lentävän ilmassa.
Suhdelaskennassa numero viisi on tärkeä useiden asioiden yhteydessä. Nyt voi väittää hypyn korkeuden olleen viidesosan hypyn pituudesta+ maailmankaikkeuden kitka 1,03. (8,90 m / 5) x 1,03 = 1.83 m. Tiedettäessä hypyn pituuden olleen 8,90 m, on laskettavissa nimellinen hypyn korkeus.
h = 4.45 m x tan 22,5o 4,45 m = 8,90 m /2 h = korkeus
h = 1,84 m
Tästä voi määrittää hypyn keston sekunteina vapaan putoamisen kaavan mukaan.
t = NJR (h /0,5 x g)
t = NJR (1,84 m /0,5 x 9,766 m/s)
t = 0,614 s
Kokonaisaika hypylle oli 2 x 0,614 = 1,228 sekuntia
Neljäs tapa määrittää hypyn pituus
Mielipiteeni on, ettei fysiikan mukaan laskettu pallon lentorata ole oikea tapa laskea hypyn pituus. Kerron muutaman syyn, miksi olen tätä mieltä.
a) Annetut kaavat lentoradalle ovat paikalla olevaan tilanteeseen, kuten tykkiin. Entä, kun tykki sijoitetaan kaksi kertaa äänen nopeudella lentävään lentokoneeseen? Hyppääjällä on vaakanopeutena sama, kuin ns. ammuksen lähtönopeus.
b) Pienen mittakaavan laboratoriotestit antavat halutun tuloksen kaavojen mukaan.
- Testikuulan koko ja paino on suuresti ylimitoitettu kantamaan nähden.
- Kuulalle liikkeen antavan elimen (jousen?) voimaa ei oikeastaan pysty määrittämään.
- Testikuulan muoto on täydellinen, vertaa tätä hyppääjään ilmassa.
- Käännä luoti 90o ja ammu sitten kylki edellä. Nyt loppuivat kaavat.
c) Testikuula lähtee 40o - 45o kulmassa, jossa hyppääjä ei koskaan lennä ilmassa (n. 20o).
d) Ilmanvastuksen puuttuessa kaavat toimivat, mutta eivät todellisessa maailmassa.
e) Eräät sinänsä arvostettavat laskelmat lentorataan liittyen, antavat lentoajan, jonka perusteella Bob Beamon käytännössä teki myös uuden korkeushypyn ME:n. Tämä kun huomioidaan rima 4,45 m päässä ponnahduskohdasta. (901)
f) Pituushyppääjät tietävät nopeuden tärkeimmäksi tekijäksi tuloksen saavuttamiseksi. Tästä syystä on ehdotettu 100 ja 200 m ME:n omistavaa Usain Boltia rikkomaan voimassa oleva ennätys 8,95 m. Kilpajuoksija saavuttaa suurimman nopeutensa 50 -70 metrin matkalla, mutta pituushypyn juoksuradan pituus on 40 m. Onko Usain Bolt tästä syystä liian suuri 40 m pituiselle radalle?
54. Todennäköisyys samasta syntymäpäivästä
Fysiologiasta on tullut urheilusivut, jossa lasketaan fyysistä suoritusta. Seuraava esimerkki saa paikan fysiologian yhteydessä, joka on monelle tuttu. Rahaa hävitään pelien ja pelaamisen yhteydessä. Tämä, sillä ihminen ei erota todennäköisyyttä suhteellisuudesta
Kaksi jalkapallojoukkuetta asettuu vastakkain. Kummassakin joukkueessa on 11 pelaajaa eli 22 pelaajaa. Millä todennäköisyydellä kentällä on kaksi samana vuodenpäivänä syntynyttä pelaajaa? Ehdotan vedonlyöntiä, jossa lupaan voiton 2:1 suhteella ja sanon kentällä olevan kaksi samana päivänä syntynyttä pelaajaa. Koska vuodessa on 365 päivää on vedon vastaanottaneella pieni mahdollisuus hävitä veto?
Tosiasia kahden syntymäpäivän osumiseksi samalle päivälle on 50,7 %. Tämä, sillä todennäköisyyslaskennassa etsitään ihmispareja, jolloin syntyy 253 erilaista paria. Ensimmäisen pelaajan voi yhdistää keneen tahansa 22 pelaajaan ja seuraavan pelaajan puolestaan jäljelle jäävään 21 pelaajaan jne. Voittosuhde on vaatimaton, mutta mahdollisuus voittaa parempi, kuin vastapuolella.
253 parin ja 365 päivän suhde antaa viitteen todennäköisyydestä. Annettaessa mielikuvan vaikuttaa päätökseen, tulee johdatelluksi. Todellisessa tilanteessa moni todennäköisesti hyväksyisi vedon. Tämä kuvaa vaikeutta erottaa todellisuus ja mielikuva toisistaan.
54.1 Laskenta
Kentällä on 11 pelaajaa kummassakin joukkueessa. Oletuksena esimerkissä on yksi varamies joukkueessa, joka käytännössä on kolme pelaajaa. Yhteensä pelaajia on näin määrittäen 24. Todennäköisyys, että kahden henkilön syntymäpäivä osuu samalle päivälle on;
364/365 = 0,997
363/365 = 0,995
" - "
342/365 = 0,937
Laskemalla 24 murtolukua ja laskemalla niiden tulon saa todennäköisyyden 27/50. Todennäköisyys voittaa veto on silloin 54 %. Jos kentälle kokoontuisi 60 pelaajaa palkintojen jakotilaisuuteen, olisi todennäköisyys käytännössä 1, että kentällä on kaksi samana päivänä syntynyttä pelaajaa. (121)
55. Pyramidiharjoittelu
Pyramidin ideaa käytetään ihmisvartalon vahvuuden harjoittamiseen. Pyramidiharjoittelu aloitetaan käyttämällä kevyttä kuormaa ja tekemällä useita toistoja. Paino kasvaa jokaisen sarjan jälkeen, toistojen määrän laskiessa vastaavasti.
Toistoja Voimakkuus
10 70 % 1111111111
6 85 % 111111
2 95 % 11
1 100 % 1
On olemassa suuri riski vammautumisesta tekemällä toistoja maksimaalisella voimalla: sitä käytetään enemmän voiman kasvattamiseen kuin lihasten massan kasvattamiseen.
Katkaistu pyramidi
Toistoja Voimakkuus
12 60 % 111111111111
10 70 % 1111111111
8 80 % 11111111
6 85 % 111111
Katkaistu pyramidi stimuloi lihaksien suurenemista tehokkaammin kuin tavallinen pyramidi.
Käänteinen katkaistu pyramidi
Toistoja Voimakkuus
6 85 % 111111
8 80 % 11111111
10 70 % 1111111111
12 60 % 111111111111
Harjoittelun intensiivisyys on merkittävästi suurempi verrattuna katkaistuun pyramidiin. Tämä on sovelias kokeneelle urheilijalle, jolla on hyvä harjoittelutekniikka.
Kaksinkertainen pyramidi
Toistoja Voimakkuus
12 60 % 111111111111
10 70 % 1111111111
8 80 % 111111111
6 85 % 111111
6 85 % 111111
8 80 % 11111111
10 70 % 1111111111
12 60 % 111111111111
Etuja ja haittoja
+ Lisää voimaa ja lihasten kasvua
- harjoittelu vaatii aikaa jatkuvan painojen vaihtamisen vuoksi. (738)
21.6.2018*8:00 (40 - 255)
www.karikolehmainen.com
epcalculation@gmail.com |
