Vaijerin puuttuva momentti
Ohut lanka asetetaan kahden pisteen välille, joita kuvaa pisteet A ja B. Langan voi olettaa olevan kevyen, jolloin tukivoimat A ja B ovat pienet.
A = B = G / 2

 Jotta kevyt lanka ei riipu, sitä pitää vetää kokoon nähden äärettömän suurella voimalla. Langan lujuuden tulee tästä syystä olla äärettömän suuri, jotta lanka kestää vedosta aiheutuvan voiman. Tätä tilannetta ei oikeassa elämässä synny. Vastaava tilanne silti syntyy sähkövoimalinjoissa, joissa langat riippuvat. Ohuisiin lankoihin syntyy vetojännitys, mutta ei taivuttavaa momenttia. Langasta puuttuvan jäykkyyden seurauksena, langan mitoitus perustuu poikkileikkauksen pinta-alaan. Jotta kevyt lanka ei riipu, sitä pitää vetää kokoon nähden äärettömän suurella voimalla. Langan lujuuden tulee tästä syystä olla äärettömän suuri, jotta lanka kestää vedosta aiheutuvan voiman. Tätä tilannetta ei oikeassa elämässä synny. Vastaava tilanne silti syntyy sähkövoimalinjoissa, joissa langat riippuvat. Ohuisiin lankoihin syntyy vetojännitys, mutta ei taivuttavaa momenttia. Langasta puuttuvan jäykkyyden seurauksena, langan mitoitus perustuu poikkileikkauksen pinta-alaan.
Poikkileikkauksessa jossa on pieni taivutusvastus, syntyy käytännössä vetojännitys. Vaijerilla ja sähkölangalla on huono kannatuskyky, puhumattakaan työntämisestä, mutta suuri vetokyky. Veto muodostaa vetojännityksen, jolloin lanka on varsin yksinkertainen mitoittaa. Kappaleilla, jolla on jäykkyys => syntyy veto- ja puristusjännitys, jotka ovat erimerkkiset poikkileikkauksen vastakkaisilla puolilla. Keskellä on neutraaliakseli, jossa jännityksen suuruus on nolla.
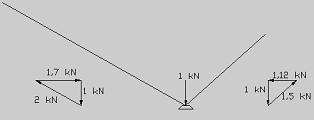 Ripustettaessa valaisin epäkeskeisesti ajoradan yläpuolelle, syntyy kuvan kuormitustapaus. Suunnittelijan suunnittelun ohjelma tekee vaijereiden voimien määrittämisen yksinkertaiseksi. Tämän jälkeen määritetään riittävä varmuus vaijerin tykyttävälle kuormitukselle. Ulkona sijaitseva valaisin kerää lunta ja tuuli heiluttaa kokonaisuutta jne. Tämä huomioidaan erityisesti lankojen päissä olevissa kiinnityksissä rakenteisiin. Edelleen huomioidaan vaijerisakkeleiden määrä kiinnityskohdissa. Vähintään kaksi vaijerilukkoa, sekä huomioidaan korroosion vaikutus lankaan. Yksinkertainenkin mitoitus sisältää useita huomioitavia asioita, jotta suunnittelija voi nukkua rauhallisin mielin yönsä. Ripustettaessa valaisin epäkeskeisesti ajoradan yläpuolelle, syntyy kuvan kuormitustapaus. Suunnittelijan suunnittelun ohjelma tekee vaijereiden voimien määrittämisen yksinkertaiseksi. Tämän jälkeen määritetään riittävä varmuus vaijerin tykyttävälle kuormitukselle. Ulkona sijaitseva valaisin kerää lunta ja tuuli heiluttaa kokonaisuutta jne. Tämä huomioidaan erityisesti lankojen päissä olevissa kiinnityksissä rakenteisiin. Edelleen huomioidaan vaijerisakkeleiden määrä kiinnityskohdissa. Vähintään kaksi vaijerilukkoa, sekä huomioidaan korroosion vaikutus lankaan. Yksinkertainenkin mitoitus sisältää useita huomioitavia asioita, jotta suunnittelija voi nukkua rauhallisin mielin yönsä.
Laskennan kannalta ihmisen väsyminen, teräskannattajan taipuminen ja monet asiat ovat samaa tarkoittavia. Jos kannattajan päälle asetetaan suurempi kuorma => lisääntyy kannattajan taipuma. Jos ihmisen kannettavaksi asetetaan suurempi taakka => kasvaa suoritukseen käytetty aika. Aika on samaa tarkoittavaa väsymisen kannalta, sillä väsyminen lisää aikaa. Urheilijan väsymisen tason voi osittain määrittää käytetyn ajan perusteella. Toisaalta jos kannattajan pituus kasvaa kuormituksen säilyessä samana => lisääntyy tässäkin tapauksessa kannattajan taipuma. Ihmisen tapauksessa etäisyyden kasvaessa => kasvaa suoritukseen käytettävä aika. Nämä asiat ovat selviä käsitteitä, laskematta niihin liittyvää samaa tarkoittavuuksia.
Aikavertailuissa kyse on usein 1-ulotteisuudesta. Mielenkiintoisesti maantiejuoksussa aika muodostuu kaikkien ulotteisuuksien kautta (ylös - alas - sivuille - aika(dilaatio). Vaijerin liike on edestakaista etenemää, köysipyörien välittäessä liikkeen eri ulotteisuuksien kautta kulkevaksi. Terästanko jäykkänä ja paikallaan olevana, ei omaa langan kaltaista materian ominaisuutta. Lanka ja sen mitoitus eivät ole oleellista, vaan viittaus langan puuttuvasta (vääntö)momentista. Vastaavuus syntyy juoksemisen yhteydessä, jossa ns. puuttuva momentti ei estä eri ulotteisuuksia. Tämä on laskettavaa, jolloin fysiikka ja fysiologia toteavat saman. Tähän palataan pian laskennan muodossa.
9.5.2015*17:40 (306 - 1091)
www.karikolehmainen.com
epcalculation@gmail.com |