Näkemisen geometria
Sisältö
1. Johdanto näkemisen geometriaan.
2. Kuun halkaisija silmämääräisesti.
3. Rauta alkuräjähdyksen jälkeen
4. Kheops pyramidi - sijainti.
5. Kheops pyramidi - valonnopeus
6. Aikadilaatio Pascalin kolmiossa
7. Platonin luolavertaus
8. Tilan täyttäminen.
9. Laskennan jakaantuminen
10. Pythagoraan viisikulmio
11. Numero viisi suhdelaskennassa.
.............................
20. Äiti ja lapsi esimerkki.
21. Euklidinen geometria
22. Suhdelaskenta näkemisen geometriana
23. Luonnon modulaarinen ajattelu.
24. Suorakulman suhteellisuus
25. Piste
26. Pii 3,14 jokien pituus
27. Ympyrän kuvaaminen
27.1 Ympyrä ja ellipsi
27.2 Oleta Pyöreä Lehmä
27.3 Teräsympyrän kuvaaminen
28. Ympyrän ja neliön pinta-alat
29. Kultainen leikkaus 1,618 ympyrässä.
30. Tasasivuinen kolmio ja ympyrä
31. Valonnopeus näkemisen geometriana
32. Viisikulmion kulmat
.....................
39 Viisikulmio appelsiineissa.
40. Viisikulmio omenoissa
41. Viisikulmio kädessä
42. Viisikulmion pinta-alat
43. Johannes Kepler; ellipsikuvaus planeettojen kiertoradoista
44. Ellipsin piirtäminen
44.1 Ellipsin piirtäminen narun ja kahden nastan avulla
44.2 Ellipsin piirtäminen kahden ympyrän avulla
45. Ellipsi ympyrässä
46. Maailmankuvan ympyröiden pinta-alat
46. Kitkan kerroin 1,03.
48. Maailmankaikkeuden kitka.
49. Pysähtymismatka näkemisen geometriana
50. Pyramidin tilavuus
....................
59. Pascalin kolmio - fii 1,618
60. Pallon tilavuus
60.1 Pallon tilavuus; kaava
60.2 Pallon tilavuus; suhdelaskenta
60.3 Pallon tilavuus; kultainen leikkaus ja gravitaatio
60.4 Pallon tilavuus; Kone-elimien elinikä
60.5 Pallon tilavuus; Ympyrän pinta-ala / (π / 1,034)
61. Pascalin kolmio & pii (3,14)
61.1 Luonnon kerroin 1,1
62. Fibonaccin lukujono
- Kultainen leikkaus
63. Kultainen leikkaus tuotteissa
64. Teräksen ominaispaino
65. Teräksen lujuus näkemisen geometriana
65.1 Teräksen kovuuden kultainen leikkaus.
66. Lujuus näkemisen geometriana
66.1 Kultainen kolmio
66.2 Taipuman varjo
67. Tuotteet näkemisen geometriana
67.1 Nostokorvakkeet 500 - 40 000 kg
68. Fysiologia näkemisen geometriana
68.1 Lyhyet juoksumatkat Pascalin kolmiossa.
1. Johdanto näkemisen geometriaan
Eräänä päivänä meillä on laaja näkökulma laskea asioita. Nytkin voi halutessa ajatella;
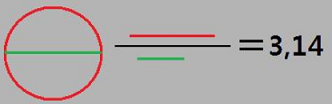
Punainen ympyrän kehämittä per vihreä halkaisija = 3,14.
Ei tarvitse tietää pituuksia tai halkaisijoita. Kaikki vastaavat kuviot sisältävät suhteen 3,14. Värit ja kuviot, ovat näkemiseen perustuva tapa ymmärtää niitä.
Yksiköt ovat ihmisten keksimiä, joten tällä ajatuksella kaikki ympyrät voivat olla halkaisijaltaan 1. Millimetrin, tuuman, jalan, mailin, valovuoden jne. halkaisijaltaan. Ympyrän koko, ei määritä yksikköä monikolliseen muotoon. Laskemme esimerkiksi ilmiöitä tuotteissa, jolloin yksikköympyrän pinta-ala määrittää teräksen ominaispainon (0,785).
A = pii x r2
A = 3,14 x 0,52
A = 0,785
Pysähdymme tähän hetkeksi havaitaksemme myös kirjaimien sisältävän tiedon ilmiöstä. Kaikki ilmiöt ovat alkujaan johdettavissa kaavasta.
E = m x c2
Energia (E) ja valonnopeus eivät tunnista massaa. Tämä on ajattelumme pääperiaate niistä
Kirjaintunnukset
Kolmeulotteisessa maailmassa kolme ensimmäistä kaavan E = m x c2 kirjaintunnusta ovat tunnettua. Paine voi muodostua materiasta tai lähes aineettomasta väliaineesta. Massa pinta-alan päällä muodostaa kaksiulotteisen paineen pinta-alan ja materiaalin välille. Paineilmapullon tapauksessa, massa on pieni, mutta kolmeulotteinen paine voi olla suuri.
L = pituus A = Pinta-ala V = Tilavuus P = paine
Ilmiöt/ Phenomena
1. On olemassa ilmiö muodoltaan ympyrä (d1)
Ympyrä on symmetrinen, jolloin sen leveys on sama kuin sen korkeus.
Ympyrän pinta-ala; A = Pii x r x r (Pii = 3,14)
A = 3,14 x 0,5 x 0,5
A = 0,785
2. On olemassa ilmiö muodoltaan neliö (1 x 1)
Neliö on symmetrinen, jolloin sen leveys on sama kuin sen korkeus.
A = 4 x 0,5 x 0,5
A = 1
Huomataan 3,14 / 4 = 0,785
(Laskemme esimerkiksi ilmiöitä tuotteissa, jolloin yksikköympyrän pinta-ala määrittää teräksen ominaispainon (0,785))
3. On olemassa ilmiö muodoltaan ellipsi 1,6 x 1 (r = 0,8 ; s = 0,5)
A = pi x r x s
A = 3,14 x 0,8 x 0,5
A = 1,25
Sanomme ilmiöiden olevan toisensa pois sulkevat, koska ilmiöt poikkeavat toisistaan. Onko näin, sitä tarkastelemme hetken aikaa. Tunnette mainitut kolme geometrista muotoa, joten niitä ei esitetä tarkemmin. Ilmiön geometrista muotoa tuskin osaatte ajatella, joten kerron niiden käyttäytyvän, kuten laskelmat osoittavat geometristen kuvioiden yhteydessä. Pinta-ala on kaksiulotteista, jolloin kaksiulotteisuudessa (ilmiön) kasvaminen kaksinkertaiseksi tarkoittaa suuruutta nelinkertaisena. Tämä tiedetään, mutta niin kasvaa kasvaa myös arvo 0,785 eli 4 x 0,785 = Pi (3,14). Ellipsin päämitat 1 ja 1,6(18) ovat kaikkeen luonnossa liittyvä suhde. (881)
1 + 0,618 = 1,618
1 / 1,618 = 0,618
2. Kuun halkaisija silmämääräisesti
 Taivaankappaleen mittaamiseen tarvitaan laite, jonka rakenne kuvataan seuraavassa. Reikälevy, jollaista suunnittelija käytti piirtäessään ympyröitä piirustuksiin. Lisäksi on metrin pituinen nauha. Osat eivät paljon maksa. Nämä ovat tarpeeksi määrittämään kuun halkaisija. Taivaankappaleen mittaamiseen tarvitaan laite, jonka rakenne kuvataan seuraavassa. Reikälevy, jollaista suunnittelija käytti piirtäessään ympyröitä piirustuksiin. Lisäksi on metrin pituinen nauha. Osat eivät paljon maksa. Nämä ovat tarpeeksi määrittämään kuun halkaisija.
Aseta reikälevyn 10 mm = 1 cm reikä 111 cm päähän silmästä. Mikä tahansa 10 mm reikä käy tähän. Kuu mahtuu juuri reiän sisään. Laske kuun halkaisija tiedon perusteella. Kuun on keskimäärin 384 400 km päässä maasta. Kuun halkaisijaksi kirjallisuus antaa 3470 km. Mittausvirhe 0,2 %. Esimerkki antaa kuvauksen suorasta lineaarisesta suhteellisuudesta. (288)
1 cm = x => x = 3463 km
111 cm 384 400 km
1 - 1,12 - 1,25 - 1,6
3. Rauta alkuräjähdyksen jälkeen
Ei tarvitse mennä kauemmaksi kuin alkuräjähdykseen, kun luku viisi tulee vastaan ja myöhemmin ymmärrettävällä tavalla kultainen leikkaus määrittää Pascalin kolmion nimellä tunnetun kuvion. Kuvion joka tunnetaan, mutta jota ei ymmärretä ilmiöihin liittyväksi.
Lujuuden laskemiseksi tarvitaan materaali rauta, jota on maapallolla alkuaineista eniten. Rauta, nimitykseltään teräs on materiaali tähän tarkoitukseen. Suhdelaskennan viisi porrastusta on suhteellisuusraja arvoissa ja rauta sijoittuu tälle porrastukselle, lämpötilana 4000 Kelviniä. Painavampi materiaali kuin rauta tarvitsee muodostuakseen ydinfuuusion. Pysymme teräksessä (S235 ja S355) eli lämpötilassa 106 Kelviniä, kuten taulukko osoittaa. Alkuaineista kevyemmät kuin teräs muodostavat 99.99997% tähtien koostumuksesta. Terästä painavammat alkuaineet ovat pieni vähemmistö, mutta niiden määrä on kaksi kolmasosaa alkuaineista.
Metallien muodostuminen
Ydinreaktio Lämpötila 106 K Pascalin kolmio
0. Vety -> helium 10 - 40 1
1. Helium -> hiili, happi 100 -200 1 1
2. Hiili -> neon, natrium, magnesium 800 1 2 1
3. Neon -> magnesium, pii 1 700 1 3 3 1
4. Happi -> pii, rikki 2 100 1 4 6 4 1
5. Pii -> titaani, sinkki, nikkeli, rauta 4 000 1 6 1 1 6 1
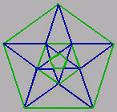 Pascalin kolmion alin rivi on järjestyksessä viides rivi lähtöarvosta 0. Rivin viisi havaitsee kultaiseksi leikkaukseksi 1,618, vaikka poikkeaa hieman arvosta 1,618. Pascalin kolmion alin rivi on järjestyksessä viides rivi lähtöarvosta 0. Rivin viisi havaitsee kultaiseksi leikkaukseksi 1,618, vaikka poikkeaa hieman arvosta 1,618.
Viidennettä alkuainetta kuvaa viisikulmio, jossa kultainen leikkaus esiintyy monessa. Tätä kuvataan näkemisen geometriassa ja lujuuslaskennassa. (594)
4. Kheops pyramidin sijainti
Suuri pyramidi 2560–2540 eaa. (Khufu tai Kheops kreikaksi) Gizassa, Egypti, osoittaa merkittävän luonteensa sen sijoittumisessa maanpinnalla. Pyramidi sijaitsee mantereiden painopisteessä. Se sijaitsee tarkasti keskellä kaikkia maa-aluita maailmassa, jakamalla maapallon maapinta-alan suunnilleen yhtä suuriin neljäsosiin. Tämä on näkemisen geometriaa, jota muinaisest ihmiset toteuttivat monumentaalisella rakennelmalla.
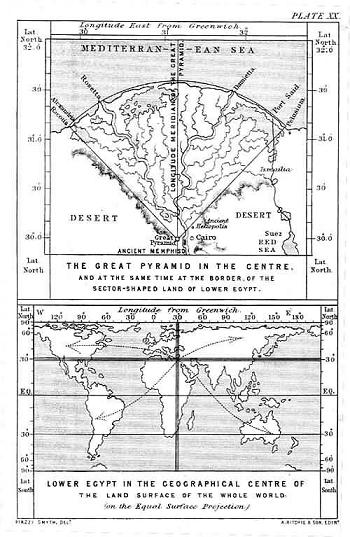
Pyramidin sijainti maapallon suurimmassa massakeskittymässä
5. Kheops pyramidi - valonnopeus
Pyramidin pohjan mitat ovat 230,3 m x 230,3 m
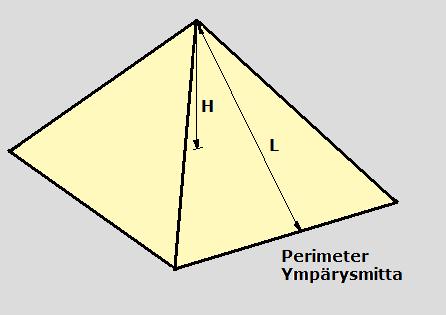
Piirretään kaksi ympyrää pyramidin ympärille, toinen ulkopuolelle pyramidia ja toinen sisäpuolelle, kuten piirustus osoittaa.
Ulkopuolisen ympyrän kehän pituus - sisemmän ympyrän kehän pituus = valonnopeus
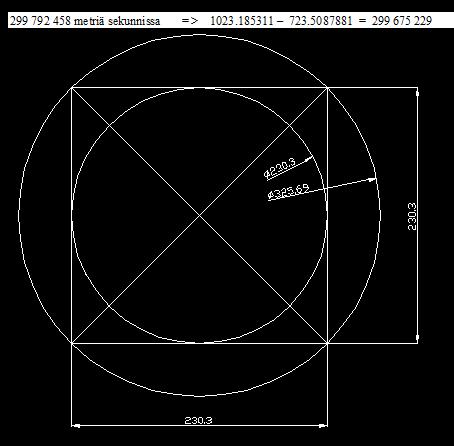
Pii x 230,3 = 723,509
Pii x 230,3 x sgrt (2) = 1023,196
1023,196 - 723.509 = 299,687
(Valonnopeus 299 792 km/s)
Ollaan laskelmasta mitä mieltä vain, se kieltämättä osoittaa yhtäläisyyden valonnopeuteen.
(831)
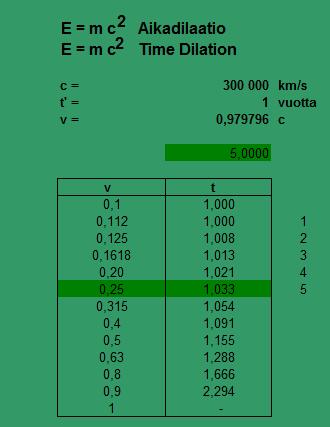
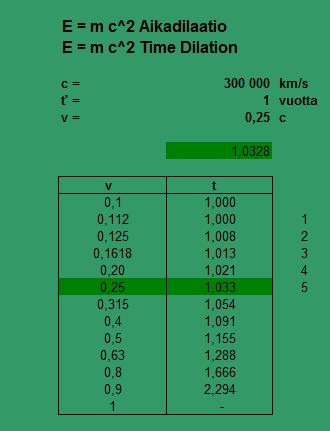
6. Aikadilaatio Pascalin kolmiossa
E = m c2
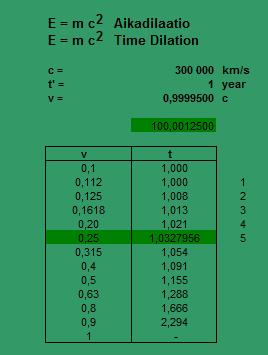
Aikadilaatiotaulukko

Pascalin kolmio näkemisen geometriana
1 dim 1 m (1,0328)
2 dim 1 1 m2 1,03283
3 dim 1 2 1 m3 1,03286
4 dim 1 3 3 1 s / t 1,03289
1,03283 = 1,1 - 1,03286 = 1,21 - 1,03289 = 1,337
Taustaa

Teoria suhteellisuudesta
Sata vuotta erityisen suhteellisuusteorian jälkeen, teoria suhteellisuudesta täydentää yleistä suhteellisuusteoriaa ja selittää, kuinka tähtitieteellisissä mittakaavoissa tunnistetut asiat vaikuttavat maan päällä pienellä nopeudella. Tämä esitetään samaa tarkoittavana suhdelaskentana.
Ensimmäinen peruste on Albert Einsteinin teoria, jota ei ole käytetty pienellä nopeudella tapahtuviin ilmiöihin, vaikka seuraava lause kehoittaa tähän.
Erityinen suhteellisuusteoria koskee kaikkia fysikaalisia ilmiöitä paitsi painovoimaa
Toinen peruste on aikadilaation liittyminen maan päällä tapahtuviin ilmiöihin
Liikemäärä p muuntuu Lorenz-muunnoksessa tekijällä 1/L, kun L = sqrt (1-( v/c )2)
==> aikadilaatio 1,0328 valonnopeudella 0,25 c
7. Platonin luolavertaus
Näkemisen geometrian historiallinen tausta on tuhansia vuosia taaksepäin, esitettävän laskennan ollessa tätä päivää. Kirjoitan historiasta ja tämän päivän todellisuudesta, josta vanhimman kuvauksen antaa Platon. Tämä kuvaus tarkennettuna aloittaa myös fysiikan toiset perusteet kirjoituksen. Lopulta varsin monet asiat ovat geometriaa, jonka tulemme toteamaan.
 Platon käytti tunnettua luolavertausta, verraten asemaamme luonnon kaavion suuressa luolassa asuvaan ihmiseen. Vertauksen todellisuuden kuva syntyy esineiden muodostamina varjoina luolan seinälle. Tämä tapahtuu siten, että todelliset esineet auringon valossa, vaihtoehtoisesti nuotion valossa heittävät varjon luolan takaseinälle. Luola-asukkaiden tavoin nykyihminen raapii todellisuuden pintaa aistiensa ja kykyjensä rajoissa. Lisää tästä voi lukea fysiikan sivuilta. Platon käytti tunnettua luolavertausta, verraten asemaamme luonnon kaavion suuressa luolassa asuvaan ihmiseen. Vertauksen todellisuuden kuva syntyy esineiden muodostamina varjoina luolan seinälle. Tämä tapahtuu siten, että todelliset esineet auringon valossa, vaihtoehtoisesti nuotion valossa heittävät varjon luolan takaseinälle. Luola-asukkaiden tavoin nykyihminen raapii todellisuuden pintaa aistiensa ja kykyjensä rajoissa. Lisää tästä voi lukea fysiikan sivuilta.
8. Tilan täyttäminen
Ajatus tilan täyttämisestä samankaltaisilla kappaleilla on 2300 vuotta vanha. Tiettävästi ensimmäisenä asiaa pohti Platon (427 - 347 eKr.). Platonin mukaan aine muodostui tilan täyttävistä monitahokkaista, määrittäen viisi säännöllistä monitahokasta ja kutsuen näitä viideksi säännölliseksi kappaleeksi. Nämä edustivat hänen näkemystä avaruusgeometrian täydellisestä symmetriasta.
Kuviot Wikipediasta
 Säännöllinen kappale on monitahokas, jossa kaikki tahkot ovat kooltaan ja muodoltaan samat ja jossa vierekkäisten tahkojen väliset kulmat ovat samat. Kuutio on hyvä esimerkki. Siinä tahkot ovat neliön muotoiset, samoin vierekkäisten tahkojen kulma on aina 90 astetta. Todistus siitä, että on olemassa ainoastaan viisi tällaista kappaletta on kreikkalaisten suuri matemaattinen saavutus. Säännöllinen kappale on monitahokas, jossa kaikki tahkot ovat kooltaan ja muodoltaan samat ja jossa vierekkäisten tahkojen väliset kulmat ovat samat. Kuutio on hyvä esimerkki. Siinä tahkot ovat neliön muotoiset, samoin vierekkäisten tahkojen kulma on aina 90 astetta. Todistus siitä, että on olemassa ainoastaan viisi tällaista kappaletta on kreikkalaisten suuri matemaattinen saavutus.
Platonin kuuluisin oppilas Aristoteles esitti, ettei opettajansa käsitys voinut olla oikea. Tämä perustui siihen, ettei moni viidestä monitahokkaasta täyttänyt tilaa kokonaan, vaan jätti tyhjän tilan pakattaessa ne tiiviisti. Ainoastaan kuusitahkoiset kappaleet eli kuutiot ja neljätahkoiset tetraedrit täyttivät tilan täysin. Muihin jäi aukkoja. Jostakin syystä tetraedri täytti Platonin ajatuksen täydellisen tilan täyttämisestä? Käsitys tetraedrin mahdollisuudesta täyttää tila kokonaan, säilyi 1800 vuotta. Tänään tiedämme ainoastaan kuusitahkoisen kuution voivan täyttää tilan kokonaan. Saavumme numeroon viisi.
Säännöllisiä monitahokkaita on yhdeksän:
Viisi Platonin kappaletta
Neljä Kepler–Poinsot'n kappaletta ovat tähdenmuotoisia säännöllisiä monitahokkaita. (57)
9. Laskenta jakaantuu kahteen tarkastelutapaan ilmiöissä
a) Tarkastelut laskemalla ilmiöitä määrittäen, laskennan pyrkiessä välttämään kaavoja.
b) Tarkastelut kuvioista, jolloin kuviot paljastavat saman kuin laskemalla. Menettely saa usein esiin sellaista, mitä emme kykene laskemaan.
Visuaaliset kuviot varjoina todellisuudesta
Viisikulmio kuvaa ihmistä. Siinä on kaksi jalkaa, kaksi kättä sekä pää. Kuva ilmaisee ihmisen mittasuhteet, josta enemmän fysiologian kirjoituksessa. Ei vain ihmisen, vaan kaiken olevaisen konstruktion.
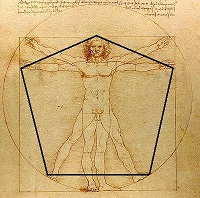
Leonardi da Vinci, Vitruviuksen mies
Ellipsi on erityinen matemaattisen muodon luokka sen muistuttaessa venytettyä ympyrää. Ellipsissä on kaksi polttopistettä. Ympyrä puolestaan on ellipsin erikoistapaus, siinä ovat molemmat polttopisteet yhtyneenä keskipisteessä.
10. Pythagoraan viisikulmio
Viisikulmio on symmetrinen viisipisteinen tähtikuvio, johon sisältyy viisikulmio. Pythagoraasta lähtien viisikulmio on ollut tutkituin kuvio kultaisen leikkauksen yhteydessä. Nykyään Pythagorasta ei yhdistetä viisikulmioon, vaan Pythagoraan lauseeseen. Pythagoras ei liity edes hänen nimissään olevaan lauseeseen, sillä hypotenuusan ja kateettien välinen suhde oli tunnettu tuhat vuotta ennen Pythagorasta. Tiettävästi pentagrammi eli viisikulmio esiintyi ensimmäisenä sumereilla noin 3000 eaa. Eri asia on, kuinka Pythagoras tulkitsi viisikulmiota ja onko sille todistetta. Viisikulmion tiedetään sisältävän lukusuhteen 1,618 monessa merkityksessä. Näiden havaittujen ominaisuuksien vuoksi Pythagoras otti viisikulmion jumalalliseksi symboliksi perustamalleen salaseuralle. Muun muassa Kheopsin Pyramidi muodostaa kultaisen leikkauksen lukusuhteen 1,618. Mainitsen pyramidit siksi, että Pythagoras matkusti Egyptiin ja tutustui siellä näihin rakennelmiin ja myös egyptiläisten matematiikkaan, joka perustui pitkälti geometriaan.
Tästä ei ole todistetta, mutta ajatellaan näin. Pyramideista voi todeta niiden olleen tuhansia vuosia vanhoja, Pythagoraan vierailtua maassa. Rakennelmat, joiden valmistusta ei kyetä vieläkään selittämään tai toistamaan taloudellisten resurssien puutteessa. Egyptiläisten matemaattista osaamista on väheksytty, sen sanottua liityttyneen suuressa määrin Niilin tulvimiseen ja tästä johtuvaan maa-alojen määrittämiseen viljelijöille. Tiivistettynä egyptiläisten sanotaan yhdistäneen määrän ja muodon matematiikassa. Voidaan sanoa egyptiläisten määrittäneen massaa (viljaa) pinta-alaan, jonka sivut neliönä ovat a kertaa a, josta saatiin sato. Eräässä myöhemmin tunnetussa kaavassa "sato" energiana saadaan kertomalla massa pinta-alalla, joka on kateetiltaan valonnopeus. Tämä tiivistyy muotoon E = m c c. Tästä kerron lisää sivuillani, mutta ensin viisikulmioon.
Avaan viisikulmiota kertomalla historiasta, lujuuden muodostumisen materiassa, sekä esitän laskentaa tuotteissa suhdelaskentana. Useat asioista, jotka ovat laskettavia, ovat esitettävissä geometrisena kuvioina. Tämä, sillä luonto paljastaa arvoja kuvioina ja esittää harmonian niiden välillä.
Lähtökohta on energia, josta materia jäähtymisen jälkeen on tiivistyi. Materia perustuu energiaan, joka meille on silmin havaittavaa massaa. Voimme laskea massaa ja energiaa, niiden ollessa samaa tarkoittavia. (851)

11. Numero viisi suhdelaskennassa
 Laskenta tutustuttaa viisikulmioon ja kirjoituksiin Pythagoraasta? Jotkin kirjat varoittavat tämän kaltaisesta ajattelusta, ikään kuin numeroihin tai kuvioihin sisältyisi matemaattisen olion käsite. Silti muutama nimi Leonardo da Vincistä eteen- ja taaksepäin ovat huomioitavaa numero viiden ja suhdeluvun 1,618 yhteydessä. Näkemisen geometria on laskennallinen todellisuus, josta on kirjoitettu. Laskenta tutustuttaa viisikulmioon ja kirjoituksiin Pythagoraasta? Jotkin kirjat varoittavat tämän kaltaisesta ajattelusta, ikään kuin numeroihin tai kuvioihin sisältyisi matemaattisen olion käsite. Silti muutama nimi Leonardo da Vincistä eteen- ja taaksepäin ovat huomioitavaa numero viiden ja suhdeluvun 1,618 yhteydessä. Näkemisen geometria on laskennallinen todellisuus, josta on kirjoitettu.
Seuraavaksi kirjoitetun liittymättä aiheeseen, liitän sen tästä huolimatta tähän. Minusta on vain hauska tehdä se tässä yhteydessä. Tiedätte Leonardo da Vincin tunnettuna taiteilijana ja pystytte luettemaan hänen teoksiaan. Tehkää se, jolloin toteatte sen mahdottomaksi. Muutama säilynyt maalaus (n. 15 kpl) hänen muistiinpanojensa ohessa, joihin kuuluu piirustuksia, tieteellisiä kaavioita ja ajatuksia maalaustaiteen luonteesta. Nämä muodostavat merkittävän panostuksen myöhemmille taiteilijoille, jolloin sen kanssa kilpailee vain hänen aikalaisensa Michelangelo. Leonardo da Vinci oli siten eräs maalaustaiteen merkittävimmistä taiteilijoista, olematta varsinaisesti taidemaalari.
Ovatko kenties käsitykset ilmiöistä samaa tasoa tietämyksen kanssa Leonardo da Vincistä? Tiedetään paljon, mutta ei tiedetä kaikkea. Mikäli laskukone kädessä ei esitä saman kuin kirjoitan, voitte poistua sivuiltani. Suon sen teille mielihyvin, siirtyäksenne takaisin fantasiaan. Edellinen, sillä uskon laskimen kertovan enemmän todellisesta maailmasta, kuin erilaiset aatemaailmat todistamattomina.
Ympyrän pinta-ala
a) Säde - r = 1
A = π x r2 = 3,14
b) Säde - r = 2
A = π x r2 = 12,566
Täysympyrä 360o
2 x π = 6.28 rad rad.
1 - 1.03 - 1.06 - 1.12 - 1.25 - 1.6 - 2 - 2.5 - 3.15 - 4 - 5 - 6.3 - 8 - 10
6.283 rad / 2 = 3.14 rad
1 - 1.03 - 1.06 - 1.12 - 1.25 - 1.6 - 2 - 2.5 - 3.15 - 4 - 5 - 6.3 - 8 - 10
3.14 rad / 2 = 15707
1.5707 rad = > 1.03 x 1.5707 = 1.618 rad
1 - 1.03 - 1.06 - 1.12 - 1.25 - 1.6 - 2 - 2.5 - 3.15 - 4 - 5 - 6.3 - 8 - 10
NJR ( 1.5707 ) = 1.253
6.283 rad / 5 = 1.256 rad
1 - 1.03 - 1.06 - 1.12 - 1.25 - 1.6 - 2 - 2.5 - 3.15 - 4 - 5 - 6.3 - 8 - 10
NJR ( 1.2533 ) = 1.12
1 - 1.03 - 1.06 - 1.12 - 1.25 - 1.6 - 2 - 2.5 - 3.15 - 4 - 5 - 6.3 - 8 - 10
NJR ( 1,12 ) = 1.06
1 - 1.03 - 1.06 - 1.12 - 1.25 - 1.6 - 2 - 2.5 - 3.15 - 4 - 5 - 6.3 - 8 - 10
NJR ( 1,06 ) = 1.03
1 - 1.03 - 1.06 - 1.12 - 1.25 - 1.6 - 2 - 2.5 - 3.15 -4 - 5 - 6.3 - 8 - 10
NJR = neliöjuuri
Edellä esitetty on näkemisen geometriaa ja laskelmia, ilman nähtäviä kuvioita. Emmehän näe ilmiöitäkään, vaikka ne varmuudella ovat olemassa. Ilmiöiden seuraukset sen sijaan tunnemme hyvin. Ne omaavat monessa tapauksessa yllä olevan muodon tavalla tai toisella. Miksi sivun otsikon nimenä on "numero viisi", vaikka sitä ei esiinny sivulla. Syynä on se, ettei kaikki ole nähtävää. Voisin kertoa viidestä sormesta, jolla avasitte tietokoneen. Viidestä sormesta, johon tukkimiehen kirjanpito perustuu ja jatkaa tämän sivun viisikulmioon. (125)
20. Äiti ja lapsi esimerkki
Tässä ajassa on mahdollista vertaus, jossa joku piiloutuu kiven taakse. Tarkoitukseen soveltuu lapsi. Lapsi on kiven takana, ajatellen olevansa kätkeytynyt. Sen lisäksi, että äiti tietää lapsen olemassaolon yleisesti - kuten tunnemme asioista ja arvoista niiden olemassa olon yleisesti - äiti näkee lapsensa varjon kiven takaa. Tähän tarvitsemme Platonin luolavertauksen mukaisesti valonlähteen, auringon.

Aika on tapahtuman varjo
Lapsi on kippurassa, josta äiti osaa päätellä jännittävän hetken lapsen elämässä. Edelleen äiti näkee varjosta lapion lapsen kädessä ja päästä pudonneen hatun - jota ei ole lapsen päässä - tietäen hatun olleen päässä. Samalla tavoin voi nähdä asioita arvoista ja tuotteista, osatessa tulkita niiden merkityksen. Ei tarvitse nähdä lasta, joka vertauksena kuvaa ilmiöitä, valmistettavia tuotteita jne. Varjo on jotakin, jota ei voi koskettaa, kuten aikaa urheilutuloksen yhteydessä. (774)
21. Euklidinen geometria
Geometriaa ei ole geometrian vuoksi, vaan todellisuudessa tarvittavien määritysten vuoksi. Ymmärrämme geometrian pinta-alojen ja tilavuuksien laskemiseksi, silti kaikki on lopulta pinta-alaa. Kykenemällä määrittämään pinta-alan, määrität muun.
Energia M = m c2 Valon nopeuden peitto
Paine kg/cm2 Paineen peitto
Jännitys kN/cm2 Voiman peitto
Nopeus m/s2 Kiihtyvyyden peitto
Eukleides kirjoitti
Voidaan piirtää suora viiva mistä tahansa pisteestä mihin tahansa pisteeseen
Näkemisen geometria; käyrän voi piirtää minkä tahansa kahta useamman tapahtuman välille, jos nämä tunnetaan. Suhdelaskennalla, jopa tapahtumiin joita ei edeltä käsin tunneta.
Asiat vastaavina samaan asiaan ovat myös vastaavia toiseen
Näkemisen geometria; geometria pinta-alan käsitteenä, laajentuu ilmiöihin ja tapahtumiin. Eukleides näki kauemmaksi tässä lauseessa. Geometriasta lauseessa ei mainita sanallakaan.
Ääripäät viivoissa ovat pisteitä
Näkemisen geometry; tapahtuma tai ilmiö on piste käyrän alkupäässä, välillä ja lopussa. Käyrä määrittyy äärettömästä määrästä pisteitä.
Viiva on yhtäjaksoinen pituudeltaan
Näkemisen geometria; kahden tapahtuman tai ilmiön välillä ei ole tyhjiötä tai aukkoja
Suorassa piilee yhdenvertaisesti pisteitä itselleen
Näkemisen geometria; käyrällä piilee yhdenvertaisia tapahtumia ja ilmiöitä suhteellisesti yhdenvertaisina toisilleen. (733)
22. Suhdelaskenta näkemisen geometriana
Samaa tarkoittava suhdelaskenta on lähestymistapa ymmärtää maailman rakenne, merkityksessä koskettaen arkipäivän elämää. On hätkähdyttävää lukea kolmesta lähestymistavasta ja havaita kirjoittavani kahdesta viisikulmiosta puuttuvasta laskennan menettelystä. Koska nämä ovat sivuni, voin näin kirjoittaa. Ymmärrän ajatuksena neljä viidestä lähestymistavasta, kategoriateorian avautumatta. Tämän tarkoittamatta, että laskennalla ei olisi paikkaa muiden rinnalla. (341)
Suhdelaskenta Näkemisen geometria
Joukko-oppi  Kategoriateoria Kategoriateoria
Matemaattinen logiikka
Kuva alla Wikipedia, josta saatavana lisätietoa laskentatavoista
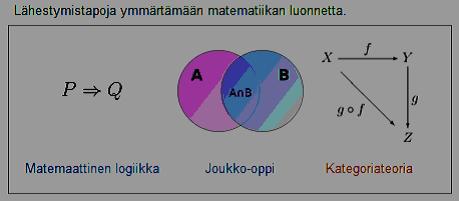
23. Luonnon modulaarinen rakenne
Kuvittele sinisellä merkityt viivat teräsputkiksi ja rakenteen muodostavan kattoansaan puolikkaan. Putkien suhteelliset pituudet ovat 1, 1,618 ja 2,618. Putket muodostavat moduulin, jolloin rakenteen voi valmistaa kolmesta eripituisesta putkesta. Putkien väliset kulmat ovat 36, 72 ja 108 astetta eli kulman 36 astetta kerrannaisia. Lopulta 5 x 36 astetta = 180 astetta = pii() radiaania. Täyskulma 10 x 36 astetta = 360 astetta = 2 pii() radiaania = 6,28.
1,618 x 1 = 1,618 => 1,618 x 1,618 = 2,618 => 2,618 - 1 = 1,618
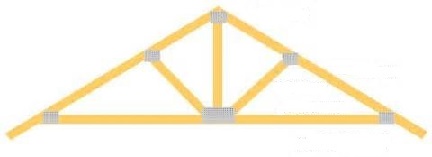
Luontoon liittyy symmetrian käsite. Vasemman puoleisen ollessa tunnettua, oikea puoli tunnetaan samassa. Ajatteletteko luonnon tekevän tukirakenteensa eritavalla, kuin me ihmiset niitä teemme? Rakenteet luonnossa näyttävät erilaisilta, mutta oletteko laskeneet niitä? Ei, ette ole, mutta kattoansas on teille tuttu. Kyllä, ne ovat tuttuja monille meistä, mutta emme ole niitä lujuuslaskeneet.
Laskennan edistyttyä, kuormitetaan ansas ja tarkastellaan voimien jakaantuminen. Vain rajoittunut mieli määrittää kuvassa olevan kattoristikoksi. Vastaavan ristikkorakenne on arvoissa ja ilmiöissä, niiden laskemisen olematta tunnettua. Samaa tarkoittavan suhdelaskennan myötä, kuviot ja kaavat tulevat samaa tarkoittaviksi. Kaikki on pinta-alaa, pituutta, tilavuutta ja aikaa. Olemme tekemisissä näkemisen geometrian kanssa. Tarkasteltaessa kuvioita, ei ole olemassa yksinkertaisempaa toimivaa mittasuhdetta kuin kultainen leikkaus 1,618. Lopulta luonnon modulaarinen ajattelu on teollisuuden hakema modulaarinen rakenne. Hyvänä esimerkkinä tästä Lego-palikat. (495)
24. Suorakulman suhteellisuus
 Suorakulma on kahden toisiaan vastaan kohtisuorassa olevan suoran välinen kulma 90°. Suorakulma on kahden toisiaan vastaan kohtisuorassa olevan suoran välinen kulma 90°.
Suhdelaskenta on epäeuklidista geometriaa, jossa ilmiöt suoraan kulmaan tai suorasta kulmasta poiketen muodostavat käyriä ja radiaanikulmia muodostavia kuvioita.
0,125 x 90° = 11,25° = sin 11,25° = 0,195 (1,253 x 1,0328 =2,0)
0,1618 x 90° = 14,562° = sin 14,562° = 0,251 (1,254 x 1,0328 =2,52)
0,20 x 90° = 18° = sin 18° = 0,31 (1,255 x 1,03 =3,15)
0,25 x 90° = 22,5° = sin 22,5° = 0,382 (1,256 x 1,0328 =3,94)
0,315 x 90° = 28,35° = sin 28,35° = 0,475 (1,257 x 1,0328 =4,92)
0,40 x 90° = 36° = sin 36° = 0,59 (1,258 x 1,0328 =6,16)
0,50 x 90° = 45° = sin 45° = 0,70 (1,259 x 1,0328 =7,67)
0,63 x 90° = 56,7° = sin 56,7° = 0,836 (1,2510 x 1,0328 =9,62)
0,80 x 90° = 72° = sin 72° = 0,951 (1,2511 x 1,0328 =12,0)
 Pascalin kolmion yhteydessä luvut hämärtyvät viidennnen tai kuudennen portaan jälkeen. Yllä olevassa taulukossa on havaittavissa tämä. Pascalin kolmion yhteydessä luvut hämärtyvät viidennnen tai kuudennen portaan jälkeen. Yllä olevassa taulukossa on havaittavissa tämä.
Kuusi ensimmäistä riviä menee jokseenkin tarkasti - samoin on ilmiöissä - tämän jälkeen on viiva laskennan yli. Alla oleva => ketju ansaitsee tarkastelun.
0,125 x 90° = 11,25° => sin 11,25° = 0,195 => 1,253 = 1,95 => 0,1253 = 0,0195 => arc sin 0,0195 = (1 +) 0,12 = 1,12 = 1,122 = 1,25 => 1,252 x 1,03 = 1,618 => 1,618 x 1,25 = 2 => 1,25 x 2 = 2,5 => 1,25 2,5 = 3,15 => 1,25 x 3,15 = 4 => 1,25 x 4 = 5 => 1,25 x 5 = 6,25 => 6,25 x 1,25 = 8 => 1,25 x 8 = 10
0,125 x 90° = 11,25° => cos 11,25° = 0,981.
Laskenta soveltuu energiaan liittyvään laskemiseen arvon 0.981 vuoksi, yleinen painovoima maapallolla. Desimaalit on syytä unohtaa ja keskittyä kokonaisuuden hahmottamiseen. Laskennassa virheet kumoavat toisensa. (383)
25. Piste
1 Piste geometriassa
1.1 Geometrian, topologian ja muilla näille rinnasteisilla matematiikan aloilla piste on yksinkertaisin olio, jolla muut oliot voi määritellä. Esimerkiksi viiva on ääretön joukko pisteitä
.
2. Samaa tarkoittava suhdelaskenta
 Samaa tarkoittavassa suhdelaskennassa pisteen merkitys on nollaulotteisuuden kuvaaminen geometrisesti ja sillä kuvataan ilmiön sijainti arvokäyrällä. Samaa tarkoittavassa suhdelaskennassa pisteen merkitys on nollaulotteisuuden kuvaaminen geometrisesti ja sillä kuvataan ilmiön sijainti arvokäyrällä.
Pisteiden sijainti määritetään yksiulotteisuutena eli etäisyytenä niiden välillä.
Pisteet ovat arvoavaruudessa, jossa niiden sijainti ilmiön kannalta ei ole merkityksellinen, sillä ilmiö ei kysy paikkakoordinaatteja. Painovoimakiihtyvyyden arvo kylläkin tarvitaan tarkasteluun.
3. Historia
3.1 Eukleides 300 eaa. määritti pisteen kirjassa Alkeet sanomalla, että ”piste on jotain, mitä ei voi jakaa” Ajatus heijasti Demokritoksen ajatusta atomista aineen pienimpänä osana, jota ei enää voitu jakaa.
Antiikin geometriassa mitattiin pisteiden etäisyyksiä eikä käytetty koordinaatteja pisteiden paikan ilmaisemiseksi. Pisteen paikka pidettiin yksikäsitteisenä vain, jos se voitiin kytkeä kiinteisiin pisteisiin riittävän monen etäisyyden avulla.
3.2 Suhdelaskennan periaate on pitkälti sama kreikkalaisten hyvin tunnettuihin paikkoihin. Nämä paikat määrittivät yhden pisteen paikan. Tämä on verrattavaa suhdelaskennan hyvin tunnettuun tietoon arvosta. Käänteisesti suhdelaskennassa vähintään yksi hyvin tunnettu piste määrittää muut pisteet.
26. Pii 3,14 jokien pituus
Aikanaan Arkimedes kehitti menetelmän piin arvon laskemiseksi mielivaltaisen tarkasti. Pythagoras puolestaan esitti fysiikan lain, joka paljasti erään fysiikan ilmiön, osoittaen matematiikan ja luonnontieteiden välillä vallitsevan olennaisen suhteen.

Cambridgen yliopiston maantieteen professori Hans-Henrik Stollum laski jokien pituuksia niiden alkulähteiltä jokien suulle ja sai jokien matemaattiseksi pituudeksi yli kolme kertaa nimellisen pituuden linnuntienä ilmaisten. Vieläpä, että luvuksi tuli 3,14, joka on ympyrän kehän ja halkaisijan suhde. Kyseessä ei ole jokaisen joen matemaattinen pituus vaan keskiarvo.
Albert Einstein esitti joen pyrkivän lisäämään mutkittelua, koska joen virtausnopeus kasvaa ulkokaarteen puolella. Kaaosta ei synny, sillä lisääntyvä kaartuminen kääntää joen uomaa takaisin päin ja lopulta leikkaa syntyneen lenkin. Joen oikaistua itsensä, joen viereen jää kaarenmuotoinen järvi.
Näistä järvistä muodostuu luonnon älykkäästi muovaamia tulvataskuja. Tunnettua on, että mitä tasaisemmassa maastossa joki kulkee, sitä vähemmän joki mutkittelee. Suomessa Pohjanmaan joet virtaavat tasaisella määperällä, jolloin mutkittelu on vähäisempää, mutta keväisin tulvien sitä voimakkaammin.
Esimerkeissä luku pii (3,14) tulee esiin mitä merkillisimmissä yhteyksissä. Pii (3,14) liittyy kultaisen leikkauksen suhdelukuun, eikä tässä mielessä ole irrallinen. Pii mielletään parhaiten ympyrään, sen kehän suhteena halkaisijaan. Kaikki ympyrän kehät eivät silti ole pyöreitä, esimerkkinä jokien pituus. Joen pituus alkupisteestä päätepisteseen vastaa ympyrän halkaisijaa, joen kokonaispituus ympyrän kehää. (91)
1,252 x 2 = 3,13
27. Ympyrän kuvaaminen
Pii (π) on matemaattinen vakio ympyrän kehän suhteesta sen halkaisijaan, likiarvoltaan 3,14159. Ympyrä on Euklidisen geometrian yksinkertainen muoto, jossa kaikki pisteet ovat tasossa annetulla etäisyydellä keskiöstä. Etäisyyttä mistä tahansa pisteestä keskiöön, kutsutaan säteeksi. Ympyrän voi määritellä myös pisteen uraksi yhtenäisenä etäisyytenä kiinteästä pisteestä.
27.1 Ympyrä ja ellipsi
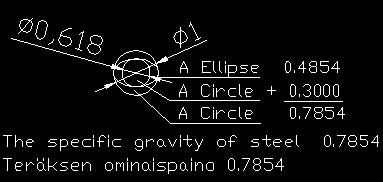
Yksikköympyrän (1) pinta-ala määrittää teräksen ominaispainon. Ympyrän sisään piirretyt kuviot kultaisen leikkauksen suhteessa, määrittävät teräksen mekaaniset ominaisuudet.
27.2 Oleta Pyöreä Lehmä
Kirjan tekijä, amerikkalainen teoreettinen fyysikko Lawrence Krauss, Art House kertoo fyysikon kauneudentajun ratkaisevasti vaikuttaneen vuosisatamme maailmankuvan muodostumiseen.
"Seinällä olevista irrallisista heijastuksista onnistuttiin jotenkin arvaamaan suorien aistimustemme taustalla oleva yhtenäisyys". Edellä oleva liittyy Platonin kuvaukseen varjoista luolan seinällä ja tietämykseen, jonka fysiikka vaikkapa hiukkasfysiikan yhteydessä tänä päivänä tutkijalle paljastaa. Tämän perusteella Platonilla oli mielessä heijastuma sähkö-magnetismin ja heikon vuorovaikutuksen olemuksesta, jotka ovat yhden fysikaalisen perusteorian erilaisia ilmentymiä.
Edellä oleva kirjoitettuna meidän ajassa. Tieteen todetessa, Platonin olleen ajatuksineen vuosituhansia ajastaan edellä. Platon käsittelee kirjoituksissa metafysiikkaa, jälkifysiikkaa. Mitä metafysiikka merkitsee, on määritelmänä tarkentamaton ja toisaalta todistamatonta. Kirjan kirjoittajan kertomana fyysikot usein aloittavat ilmiön selittämisen, piirtämällä ympyrän. Näin näkemisen geometria on aina ollut mukana tieteen tekemisessä.
27.3 Teräsympyrän kuvaaminen
Lapsen synnyttyä, ensimmäiset nähtävät muodot ovat usein pyöreän muotoisia. Valo (lamppu) seinällä tai katossa, aurinko taivaalla, kuu, pallo jne. Olettakaamme pyöreä muoto teräkselle eli yhden yksikön ympyrä. Teräksellä on yhteys alkuräjähdykseen, johtaen tästä tilanteesta laskennan perustan.
Teräksen yksikköympyrä; halkaisija ja pituus yksi yksikköä
a) Teräksen ominaispaino 7.87 g/cm3
b) teräs on rautaa, josta on poistettu hiiltä. Siinä on jäljellä muutama prosentti hiiltä, joten ominaispaino 7.87 g/cm3 on laskennan kannalta toimiva.
6,181 x 1,618 = 10 = 0,6181 x 1,618 = 1
Laskennan yksiköt eivät merkitse, niiden ollessa ihmisen keksimiä. Tässä tapauksessa suunnitteluohjelma laski painon grammoina, numeroina ilmaisten 0,618. Platonin kuuluisassa roskatynnyri esimerkissä, tynnyri heitti seinälle pyöreän varjon. Laskennassa ympyrä on mikä tahansa ympyrä halkaisijaltaan yhden yksikön. Teräksen ominaispaino on kolmeulotteinen (pinta-ala x syvyys) arvo, jonka kuvio osoittaa. (791)
28. Ympyrän ja neliön pinta-alat
Painovoima
Kuvassa on kaksi terästankoa poikkileikkaukseltaan neliö ja ympyrä. Tankojen poikkileikkaukset suhteutuvat painovoimaan ja Newtoniin (N) nimellismitalla 1, suureella olematta merkitystä. Pyöreän muodon pinta-alan laskemalla, neliön pinta-ala on tunnettu tai päinvastoin.

Ympyrän pinta-ala on 0,785 yksikköä
=> A = 0,785 x 1,25 x 1,034 = 1,02 (Newton N)
A = 0,785 x 1,25 = 9,82 (painovoima g)
Neliön pinta-ala 1,02 yksikköä on luonnollinen, sillä materiaaleissa on + toleranssi.
Phi-geometria huomioi gravitaatiovoiman ja newtonin arvon. Laskelmasta tulee samaa tarkoittava pinta-alan ja painovoiman arvoille. Näin Phi-geometria on nerokas lähestymistapa asioihin ja ilmiöihin kuvioina ja pinta-aloina. Laskenta on kuvioina esitettyä laskentaa. (30)
29. Kultainen leikkaus ympyrässa
Kultainen leikkaus
Kultainen leikkaus muodostuu maapallolla vaikuttavasta aikadilaatiokertoimesta 1,0328, joka liittyy valon nopeuteen 0,25 c. Suhdelukujen tarkkuuden vuoksi desimaaleihin ei tule kiinnittää liikaa huomiota.
1,25(2)2 x 1,0328 = 1,618
1,571 x 1,03(28) = 1,618
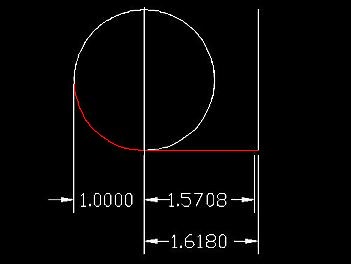
30. Tasasivuinen kolmio ja ympyrä
Uskomme suhteellisuuteen asioissa, koska toistamme sanaa suhteellisuus puheissamme. Kuvassa on tasasivuinen kolmio ja ympyrä, kykenemättä välttämään lukusuhdetta 1,618 eli kultaista leikkausta. Suhde säilyy, mitkä tahansa mitat kuvioon valitaan. Mielessä, emme niitä silloin välttämättä hahmota. Vastaava ajatus liittyy kaikkiin esitettäviin kuvioihin.
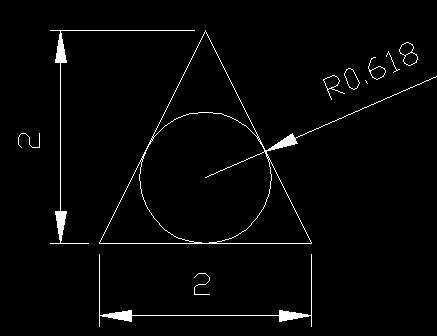
1 / 1,618 = 0,618
Näkemisen geometria hahmottaa asioita kuvioiden kautta, joita usein ei hahmota kaa-vojen kautta.
1 - 1,12 - 1,25 - 1,6 - 2,0
Kolmion pinta-ala: 2 yksikköä2
Ympyrän pinta-ala:1,1998 yksikköä2
Suhde pinta-alojen kesken
2 yksikköä2 / 1,1998 yksikköä2 = 1,6669 => 1,6669 / 1,03* = 1,618
*1,03 = kaikkeen liittyvä väsymisen kerroin aikadilaatiosta
31. Valonnopeus näkemisen geometriana
Energia saadaan auringosta, joka on pyöreä. Tunnetussa energian yhtälössä valonnopeus C on toisessa potenssissa. Sen geometrinen muoto on neliö.
Oletteko ajatelleet kuun ja auringon olevan saman kokoiset taivaalla. Kuu on 400 kertaa pienempi, mutta 400 kertaa lähempänä maata. Tämä tekee auringonpimennykset mahdolliseksi. Molemmat pyöreät muodot ovat ensimmäisiä näkemiämme lapsuudessa. Lisäksi lamppu katossa ja pallo. Tämä on näkemisen geometriaa.
Ulotteisuudet
Pituus - Pinta-ala - Tilavuus - Aika
Valonnopeus on pinta-ala c2
Valonnopeus on 3 x 108 m/s, tarkasti määrittäen 299 792 458 metriä sekunnissa.
Suhdelaskennassa valon peitto (pinta-ala) => C2 = 9 x 1016 m/s. Olemme samaa tarkoittavuudessa, jossa kultaisen leikkauksen suhdeluku 1,618 on potenssimerkintä (16).
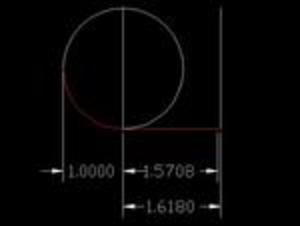
Ympyrän säteen arvo on 1 eli valonnopeus (300 000 km/s)
2 x Pii / 4 = 1,5708
1.03 x 1.5708 = 1,618
Suhdelaskennassa mikä tahansa tunnettu saa ensimmäiseksi arvon 1, jolla muut arvot määritetään. Siksi ympyrän säteen arvo on yksi eikä 3. (162)
1 - 1,25 - 1,6 - 2 - 2,5 - 3,2 - 4 - 5 - 6,3 - 8 - 10
1 / 1,6(18) = 0,63
0,25 x 0,25 = 0,63
1,25 x 1,25 = 1,56
1,57 x 1,03 = 1,62
Saatte nämä aikadilaation taulukosta
32. Viisikulmion kulmat
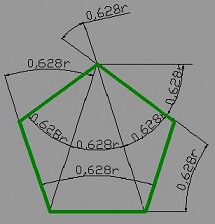 Onko mahdollista piirtää muuta kuviota, jossa symmetrisyys on kuviota vastaava? Kuvio kannattaa esittää, vaikka siihen ei sisältyisi mitään. Onko mahdollista piirtää muuta kuviota, jossa symmetrisyys on kuviota vastaava? Kuvio kannattaa esittää, vaikka siihen ei sisältyisi mitään.
0,628 radiaania kulmana on useista hedelmistä laskettava arvo. Hedelmät viestittävät täyskulman 2 pii radiaanin = 6,28 olemassaolon. Tämä vastaa 360 asteen kulmaa.
Jaetaan arvo 1 kultaisen leikkauksen suhdeluvulla => 1 / 1,618 = 0,618.
Jaetaan 0,628 radiaania arvolla 0,618 => 0,628 / 0,618 = 1,01618 Newtonia = 0,1 kg.
Jaetaan arvo 1 arvolla 1,01618 => 1 / 1,01618 = 9,84 = gravitaatiovakio 9,83 m/s2. Tästä vähennetään maan pyörimisestä aiheutuva keskipakoisvoima => painovoima g 9,82 m/s2.
Viisikulmioon on mahdollista tutustua lukuisassa määrässä suhdelaskennan tehtäviä, jolloin ymmärtää Pythagoraan kiinnostuksen kuvioon kaksi ja puolituhatta vuotta sitten. Viisikulmion särmien lukumäärä viisi määrittää ratajuoksun 200 m ME-ajan. Tunnettu tieto 100 m ME-ajaksi on 9,58 sekuntia. Tunnettua on myös, että yleisesti jännevälin kasvaessa kaksinkertaiseksi, kasvaa taipuma 23 kertaiseksi. Juoksumatkan piteneminen on ajan taipuman lisääntymistä eli kuormituksen aiheuttama lisääntyvä väsyminen. 200 metrin juoksumatka on tosin poikkeustapaus, mutta siitä myöhemmin. (604)
2 pii rad / 5 = 1,256637061
1,2566370613 x 9,58 s = 19,01 s (200 m ME 19,16 juostuna vastatuuleen. Virhe 0,78 %)
6,28 rad / 10 = 0,628 rad
Viisikulmio hedelmän keskellä

39. Viisikulmio appelsiineissa

Appelsiineissa on viisikulmion muotoinen keskiosa, jota kuvasta on vaikea havaita, sillä hedelmäliha on pehmeää. Tarkoituksellisesti kuvaa ei ole muokattu liian helpoksi.
Kuvasta voi laskea lohkojen määrän, jolloin voi yrittää löytää hedelmää, jossa lohkojen määrä poikkeaa esitetystä. Tämä sillä, joillakin ihmisillä on myös sormia poikkeava määrä.
10 lohkoa
Pythagoras, katolinen kirkko ja saatanan palvojat ovat havainneet kuvion, mutta ei tiede. Teologit yliopistossa edustavat tiedekuntaa, joten eikö tiede ole silloin havainnut kuviota? Kuinka kuvio saa näin voimakkaita ajatuksia. Kenties kuvion takana on enemmän, kuin olemme aavistaneet. (327)
40. Viisikulmio omenoissa
 Kerrotaan katolisen kirkon (ainakin joskus) kieltäneen viisikulmion esittämisen. Edellinen, sillä kuvio esittää väärin päin katsottuna saatanan palvojien tunnuksen. Todennäköisesti ette kuitenkaan leikkaa omenaa valokuvan tavalla.
Halkaistaessa omena, siementila muodostaa kukan muotoisen viisikulmion. Viisikulmion ympärille muodostuu kehä, joka on viiden kerrannainen kahdella, jolloin etäisyys kehien välillä on kultaisen leikkauksen suhdeluku 1,618. Kehän pisteiden havaitseminen on joissakin omenoissa vaikeaa. Kuvaan on merkitty viisikulmio ja ulkokehä vihreällä tussikynällä. Esitetty poikkileikkaus esiintyy muissakin hedelmissä ja viljeltävissä kasveissa. (137)
30. Viisikulmio kädessä


Etsikää se kädestä. Maailman monipuolisimmasta työkalusta. (836)
42. Viisikulmion pinta-alat
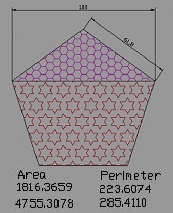 Viisikulmion yläosa on merkitty hunajakennoilla ja alaosa tähdillä. Piirustuksessa yläkolmion leveys on 100 yksikköä. Kuvion alapuolelle on merkitty näiden pinta-alat. Sama pinta-alojen suhde säilyy millä tahansa mittojen muutoksella piirustukseen. Viisikulmion yläosa on merkitty hunajakennoilla ja alaosa tähdillä. Piirustuksessa yläkolmion leveys on 100 yksikköä. Kuvion alapuolelle on merkitty näiden pinta-alat. Sama pinta-alojen suhde säilyy millä tahansa mittojen muutoksella piirustukseen.
Ajatus on sama kuin on asioissa ja ilmiöissä. Yhden tapauksen tuntemalla muut tapaukset tunnetaan. Myöhemmin havaittuna viisikulmion pinta-alojen suhteen olevan vastaava materian käyttäytymiseen kuormitettuna. Tämä on näkemisen geometriaa voimien jakautumisesta materiassa.
4755,3078 / 1816,3659 = 2,618
Viisikulmion kokonaispinta-ala
4755,3078 + 1816,3659 = 6571,6737
Kokonaispinta-alan suhde pienenpään pinta-alaan
6571,6737 / 1816,3659 = 3,618
1,618 tarkastelu
1,618 x 1,618 = 2,618
1,618 +1 = 2,618
2,618 +1 = 3,618
100 / 1,618 = 61,8
Onko olemassa muuta kuviota, jonka ominaisuudet yltävät viisikulmiolle? Kultaisen leikkauksen suhdeluku on kiistämätön kuvioon ja laskemalla tehtäviin tarkasteluihin. (335)
43. Johannes Kepler
Ellipsikuvaus planeettojen kiertoradoista
 Aikanaan auringon, kuun ja planeettojen oletettiin kiertävän maata täydellistä ympyrän muotoista rataa. Kepler hylkäsi pyöreät planeettojen kiertoradat, päätyen elliptiseen muotoon, kuten nykyään tiedetään. Aikanaan auringon, kuun ja planeettojen oletettiin kiertävän maata täydellistä ympyrän muotoista rataa. Kepler hylkäsi pyöreät planeettojen kiertoradat, päätyen elliptiseen muotoon, kuten nykyään tiedetään.
Kepler havaitsi laskelmiin perustaen planeettojen kiertoratojen olevan elliptisiä. Pienemmän akselin suhde pitempään akseliin on aurinkokunnassa 99 - 100 % paikkeilla. Pieni "episykli" planeettojen radoissa on näin pieni. Auringon sijainti on ellipsin polttopisteessä kiertoradan toisessa päässä. Tätä huomiota, ei aluksi haluttu hyväksyä.
Johannes Kepler, Wikipedia
Teidän ellipsienne takia menetetään liikkeiden ympyrämäisyys ja tasaisuus, mikä tuntuu minusta sitä mielettomämmältä, mitä syvällisemmin sitä pohdin. - Jos vain voisitte säilyttää täysin ympyrämäisen kiertoradan ja selittää elliptisen kiertoratanne toisella pienellä episyklillä, tilanne olisi paljon parempi. - Astronomi David Fabricius
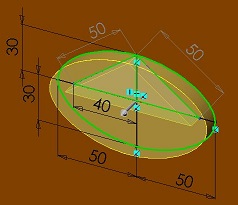
Kuvio liittyy suhdelaskentaan
Planeettojen kiertoradat ovat elliptisiä. joissa pienemmän akselin suhde pitempään akseliin on aurinkokunnassamme 99 - 100 % paikkeilla. Pieni "episykli" planeettojen radoissa on näin pieni. Auringon sijainti on ellipsin polttopisteessä kiertoradan toisessa päissä. Eräs kuvaus suhdelaskennassa on hehkulamppu, matemaattinen aurinko maan päällä. Tämä laskenta on materian ja fysiologian kuvausta, ei astronomiaa.
Ellipsin voi piirtää usealla tavalla, tarvitsematta ymmärtää piirrettyä kuviota. Tämän jälkeen voi kysyä lähes keneltä tahansa ellipsin merkitystä, siihen saamatta vastausta. Samoin käy, kysyessä ellipsin piirtämistä kynällä. (484)
44. Ellipsin piirtäminen
44.1 Narun ja kahden nastan avulla
Toisenlainen tapa piirtää ellipsi narun ja kahden nastan avulla, on seuraava kuvaus. Laita kaksi nastaa kahdeksan senttimetrin päähän toisistaan eli 80 mm päähän toisistaan. Aseta nastojen väliin 10 cm pitkä naru. Ota kynä ja aseta se punaiseen pisteeseen narua vasten. Piirrä kuvio nastojen ympäri naruun tukeutuen ja laadit ellipsinä "maailmankuvan".
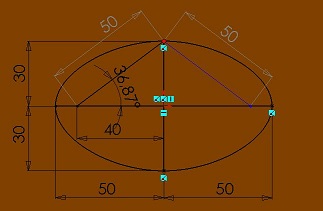
50 / 40 = 1,25
50 / (30 x 1,03) = 1,618 kultainen leikkaus
Tarkastelemme aikadilaatiossa kerrointa 1,25 ja 1,03(3), jonka kuvio esittää näkemisen geometriana.

44.2 Ellipsin piirtäminen kahden ympyrän avulla
Ellipsin voi määrittää monella tavalla, josta seuraavassa kahden ympyrän avulla, joista toinen vastaa pienempää ja toinen suurempaa akselia. Sinisellä viivalla, joka valitettavasti näkyy heikosti piirustuksessa, muodostuu ellipsi.
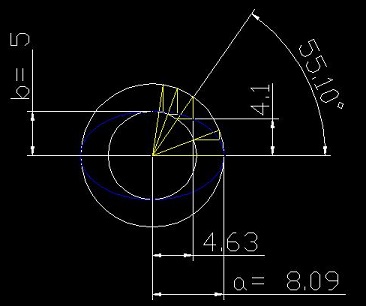
a) Ympyröiden keskipisteestä piirretään mielivaltaisesti suora suuremman ympyrän kehälle.
b) Pienemmän ympyrän viivan leikkauspisteestä piirretään vaakasuora
c) Suuremman ympyrän viivan leikkauspisteestä piirretään pystysuora
d) Vaakasuoran ja pystysuoran viivan leikkauspiste on ellipsikäyrän piste
x = a cos (kulma)°
y = b sin (kulma)°
x = 8,09 x cos 55,10° y = 5 x sin 55,10°
x = 4,63 y = 4,1
Ellipsin voi piirtää
1. Narun ja kahden nastan avulla
2. Piirtämällä harpin ja viivoittimen avulla
3. Teknisen suunnitteluohjelman avulla
4. Laskemalla
Käytännössä ellipsi piirretään teknisen piirtämisohjelman avulla, silti käsin tehtävä ellipsi on hyvä osata. Toinen asia on ellipsin liittyminen todellisuuteen. Tämä, sillä ilmiöt yleisesti ilmaisten muodostavat ellipsin. Johannes Kepler toi tämän ensimmäisenä esille taivaankappaleen kiertoradalle. Jatkamme tästä ilmiöihin. Aluksi kuviossa nähdään yksi ja myöhemmin lukematon määrä asioita näkemisen geometriana. Planeettojen kiertoradat ovat ellipsejä, joiden muotoon paneudumme vielä tarkemmin. Jotakin uutta tästä tulee avautumaan. (915)
45. Ellipsi ympyrässä
Kuviossa on suhdelaskennan periaate, jolloin tunnetulla muut tunnetaan. Kuvion mitta 0,75 määrittää ympyrän halkaisijan 1 ja ellipsin pienemmän akselin pituuden 0,5.
Ympyrän pinta-ala: 0,7854 yksikköä2
Ellipsin pinta-ala: 0,3927 yksikköä2
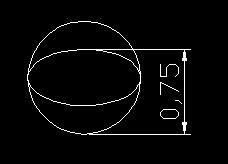
Mitta 0,5 (jota kuviossa ei näe) osoittaa ellipsin pinta-alan puolittuvan ellipsissä pyöreään pinta-alaan nähden. Minkä suhteen valitsemmekin, pinta-ala jakautuu suhteessa ympyrän ja ellipsin kesken. Tämän havaitseminen ei ole itsestään selvyys, mutta jonka näkemisen geometria pitää sisällään. Näin ympyrästä ja ellipsistä muotoutuu väline materiassa vaikuttavien voimien tarkasteluun.
46. Maailmankuvan ympyröiden pinta-alat
Johannes Keplerin havaittua maapallon kiertävän elliptistä rataa auringon ympäri. Laskenta hahmottaa vastaavuuden elliptisen muodon ja ilmiöiden välillä, jolloin elliptinen muoto liittyy tuotearvoavaruuteen. Tarkasteltaessa maailmankuvan pinta-aloja - Johannes Keplerin esittämättä sitä tässä muodossa - havaitaan kuviossa Pythagoraan kuvaama harmonia kultaisena leikkauksena. Esitetty laskenta ei ole yksin näissä havainnoissa, jotka liittyvät myös Platoniin, Johannes Kepleriin ja otamme tässä yhteydessä yhden henkilön lisää joukkoon.

Luonnon kirja on kirjoitettu matematiikan kielellä. Sen hahmot ovat ympyröitä, kolmioita ja muita geometrisia kuvioita, joita ilman ihmisen on mahdoton ymmärtää kirjasta sanaakaan. Ilman niitä hän joutuisi harhailemaan pimeässä labyrintissä. - Galileo Galilei
Geometriaa opetti koululaitos, joten sitä ei ole syytä toistaa. Koska epäilen muistikuvia opetuksesta, ellipsin pinta-ala muodostuu seuraavalla kaavalla. Yksiköillä ei ole merkitystä, sillä laskemme maailmankaikkeuden matematiikkaa.
A = pii x a x b
a = isoakselin puolikas 50
b = pikkuakselin puolikas 30
A = 3,14 x 50 x 30 = 4712,3890
Ympyrä d = 60, joka voidaan piirtää ellipsin sisään
A = 2827,4334
Ympyrä D = 100, joka voidaan piirtää ellipsin ympäri
A = 7853,9816
7853,9816 / (4712,3890 x 1,03) = 1,618
4712,3890 / (2827,4334 x 1,03) = 1,618
P.S. Kehät tarkastelemalla
Ellipsin kehä = 255,270
d 60 kehä = 188,4956
D 100kehä = 314,1593
314,1593 / (188,4956 x 1,03) = 1,618
(314,1593 + 188,4956) x 1,03/ 255,270 = 2
47. Kitkan kerroin 1,03
Valo ja varjot kätkevät samaa tarkoittavuuden. Alla olevassa kuviossa voi ajatella valon muodostavan valkoiset viivat. Tuotteet, ilmiöt ja arvot yleisesti sisältävät kitkan, jota musta väri kuvaa. Mutta, älä sano ettei geometria ole yrittänyt osoittaa kerrointa maailmankaikkeuden kitkalle.
Ilman painovoimaa ei ole liikkeen pysäyttävää kitkaa. Ilmakehä ja materia leviäisivät avaruuteen, joten maailmaa jonka näemme, ei olisi. Viisikulmio kuvaa gravitaatiovoimaa. Kerroin 9,82 josta usein Euroopassa käytetään kerrrointa 9,81.
0,3633 + 0,6181 = 0,9814
Staattisen väsymisen kerroin 1,03(4) esiintyy lukuisassa määrässä esimerkkejä ja kuvioita. Tämän voi johtaa kaavasta E = m c2. Uimme maailmankaikkeuden gravitaatiokentässä ja sen muodostamassa kitkassa, jonka voi määrittää laskemalla.
( 0,3633 + 0,6181 ) x 1,03 = 1,0
48. Maailmankaikkeuden kitka
Näkemisen geometria kuvaa monella tavalla maailmankaikkeuden kitkan.

Ympyrä halkaisijaltaan 2 yksikköä => ympyrän kehän pituus Pii x D = 6,28 yksikköä
Ympyrän neljänneksen pituus = 2 x 3,14.../ 4 = 1,5708 yksikköä
1,5708 x 1,03 = 1,618
Kultaisen leikkauksen suhteen (1,618) sanotaan olevan käsittämättömän irrationaalinen vakion. Kun jokin ilmiö, niin menetämme sen yhteydessä jotakin. Tämä jokin havaitsematon, on maailmankaikkeuden kitka asioiden välillä. Kuviossa kitka on puuttuva punaisen viivan pituus arvoltaan 1,03, joka on kitkan luonne. (854)
49. Pysähtymismatka näkemisen geometriana
Uskallan sanoa, ettei lähestymistapaa ole muualla esitetty. Alla olevassa taulukossa jarrutusmatka on laskettu fysiikan antamalla kaavalla. Reaktioaika on yleisesti hyväksytty yksi sekunti. Tästä on saatu kokonaismatka esim. nopeudella 50 km/h 26,2 m. Toinen laskentatapa oikeassa reunassa on luonnollisen logaritmin avulla.
Jarrutus kuivalla ja puhtaalla asfaltilla
Nopeus Reaktioaika Jarrutus Yht.
km/h m m m Laskenta logaritmisesti
30 8,33 4,42 12,8 Tunnettu tieto 13 m
40 11,1 7,9 19,0 40/(Ln pii)6 = 17,8 m
50 13,9 12,3 26,2 50/(Ln pii)5 = 25,5 m
63 17.5 19,5 37,0 63/(Ln pii)4 = 37 m
80 22.2 31.4 53,6 80/(Ln pii)3 = 53,3 m
100 27,8 49,2 77,0 100/(Ln pii)2 = 76,3 m
120 33,3 70,6 103,9 120/(Ln pii) = 104,8 m
125 34.7 76,6 111,3 125/(Ln pii) = 109,2 m
Näkemisen geometria

Pysähtymismatka pitenee kertoimella
1,252 /1,03(3)2 = 1,4641
kun nopeus kasvaa 25 %, pysähtymismatka pitenee, mutta lyhenee suhteellisesti nopeuden kasvaessa. pysähtymismatkakin "väsyy", kuten juoksija väsyy juostessa.
Pysähtymismatka on neljäulotteinen ilmiö, sisältäen ulotteisuudet pituudesta, leveydestä, korkeudesta ja ajasta. Aika liittyy aikadilaatioon, joka on osa arvoavaruutta. Näiden jälkeen tulee suhteellisuus asioissa, sisältäen kultaisen leikkauksen arvon 1,618.
Arvoavaruus
Pascalin kolmio
1 dim 1,1
2 dim 1,1 x 1,1 = 1,21
3 dim 1,1 x 1,1 x 1,1 = 1,331
4 dim 1,1 x 1,1 x 1,1 x 1,1 = 1,4641 Pituus - Leveys - Korkeus - Aika
Propo 1,1 x 1,1 x 1,1 x 1,1 x 1,1 = 1,61051 (Kultainen leikkaus 1,618)
Pysähtymismatkat suhdelaskemalla.
km/h Pysähtymismatka m Laskelma
30 12.8 13 m tunnettu lähtöarvo
40 19,0 13,00 m x 1,4641 = 19,03 m 1.
50 26,2 19,03 m x 1,4641 / 1,033 = 26,97 m 2.
63 37,0 26,97 m x 1,4641 / 1,033 = 38,22 m 3.
80 53,6 38,22 m x 1,4641 / 1,033 = 54,18 m 4.
100 77,0 54,18 m x 1,4641 / 1,033 = 76,79 m 5.
125 111,3 76,78 m x 1,4641 / 1,033 = 108,83 m
Pysähtymismatka nopeudesta 100 km/h:
13 m x 1,46415 / 1,0334 = 76,80 m
Laskettu 76,79 m on tarkka arvo
Suhdelaskennan tarkkuus on viisi porrastusta
Viides porrastus aikadilaatiossa ovat´arvot 0,25 ja 1,033
Moni lukija sanoo olevansa parempi jarruttaja, kuin taulukko esittää. Paras kuulemani on 21 m sadan kilometrin tuntinopeudesta. Kyseessä oli moottoripyörä, jolle poliisi mittasi jarrutusmatkan pituuden kuivalla asfaltilla. Nyt on teidän asia uskoa kertojan esitettämä jarrutusmatkan pituus, fysiikka joka tapauksessa menisi uusiksi tiedolla.
50. Pyramidin tilavuus
1/3 x Pohjan pinta-ala x Korkeus (H

Kheops pyramidi

V= 1/3 x 230,3 m x 230,3 m x 146,41 m
V = 2 588 436 m3
Näkemisen geometria
V = 1,254 x 1,06 = 2,588
( pituusx leveys x korkeus x aika x väsyminen 3d + aika)
(1,25 = 1/4)
(1,032 = 1,06)
Pramidin pinta-ala
Kaikki sivupinnat ovat samat:
Pohjan pinta-ala + 1/2 × Pohjan ympärysmitta × Kalteva pituus (L)
A = 230,3 m x 230,3 m + 1/2 x( 4 x 230,3 m) x 186,3 m
A = 138848 m2
Kultainen leikkaus
(186,3 m/146,41 m = 1,2724 => 1,27242 = 1,618 ) (737)
59. Pascalin kolmio - fii 1,618
Monet kaavat matematiikasta tieteeseen ja koneen rakentamiseen edellyttävät piitä, mikä tekee siitä yhden tärkeimmistä vakioista. Pii (3,14) määrittää yleensä pyöreän pinta-alan. Fii (1,618) puolestaan suhteen asioiden ja ilmiöiden kesken, kuten kuvan kaksi puoliskoa pyöreästä muodosta. Hajoitettaessa menetetään jotakin, kuten sahanpuru sahatessa tai vaikkapa kitka siirrettäessä. Tämä on nimeltään staaattisen väsymisen kerroin 1,03. Tällä kitkalla tai häviöllä ei ole tekemistä sen kanssa, mitä ajattelemme kahden pinnan väliseksi kitkaksi. Tämä kitka on universaalinen asioissa vaikuttava häviö. Tämän voi alustavasti todistaa alinna olevalla laskelmalla, joka muuntaa kultaisen leikkauksen 1,618 arvon ja piin keskenään yhteen. Tästä jatkettaessa useimmat ilmiöt ovat saman kaltaisella periaatteella keskenään yhteen liitettäviksi. (772)
0,1
0,1 0,1
0,1 0,2 0,1 1,6(18)
0,1 0,3 0,3 0,1
0,1 0,4 0,6 0,4 0,1
0,1 0,4 0,6 0,4 0,1
0,1 0,3 0,3 0,1
0,1 0,2 0,1 1,6(18)
0,1 0,1
0,1
0,1 + 0,4 + 0,6 + 0,4 + 0,1= 1,6
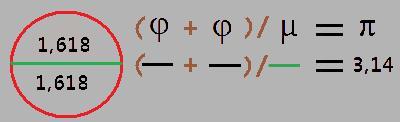
(2 x 1,618) / 1,03 = 3,14
60. Pallon tilavuus
Maapallo on pallo nimensä perusteella.
60.1 Pallon tilavuus kaavana
V = π x d3 V = 4 x π r3
6 3
V = 4,189 V = 4,189
60.2 Pallon tilavuus suhdelaskentana
V = π d3 V = π d3
2 (π /1,034*) ((1,25665 ) /1,034) x 2 Huom! 1,12(1)2 = 1,2566**
V = 4,14 V = 4,14
* 1,034 liittyy aikadilaatioon, kun valonnopeus 0,25 x C.
** 1,12 ja 1,25 ovat suhdelaskentajonon kertoimia

60.3 Pallon tilavuus; kultainen leikkaus ja gravitaatio
V = π d3 x1,618
9,82
V = 4,14
60.4 Pallon tilavuus; Kone-elimien elinikä
V = π d3
2 x 1,253
V = 4,12
Pallon tilavuuden kaavan harva muistaa. Suhdelaskennan mukaisesti pallon tilavuus on johdateltavissa. Suhdelaskennan tarkkuus on keskimäärin 2 % tarkkuus, mutta esimerkit yllä ylittävät tarkkuuden.
60.5 Pallon tilavuus
Ympyrän pinta-ala / (π / 1,034)
A = 12.566370614359172953850573533118 / (3.1415926535897932384626433832795 /1,033)
A = 4.13
Pallon tilavuus on samaa tarkoittavaa pallon poikkileikkauksen pinta-alan kanssa. Aika - väsyminen - lujuus - jännitys - tuottavuus - elinikä jne. tulevat tutuiksi ja samaa tarkoittiviksi.
61. Pascalin kolmio & pii (3,14)
61.1 Luonnon kerroin 1,1
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
Olemme lukeneet rivikertoimesta yksitoista (11), mutta onko sitä luonnossa?
Pii (π) on ympyrän kehän suhde sen halkaisijaan. Jonkin kasvaessa yksitoista kertaa suuremmaksi, sen uusi suhteellinen asema on 1,112 = 3,14. Esimerkiksi 110 cm on suhteellinen asema 1,1 pituuteen 100 cm nähden, joten kaikella on vastaava suhteellinen asema 1,1 johonkin muuhun nähden. 1,1 on mistä lähdemme ja kasvatamme sitä 1 + 11 kertaa = 12 potenssimerkintä. Pii on varjo Pascalin kolmiosta tai päinvastoin? Lopuksi esitetyn voi laskea visuualisesti kuvasta.
62. Fibonaccin lukujono
0
1 1
1 2 1 Pascalin kolmio
1 3 3 1
Viides rivi 1 4 6 4 1 16 = 1,618
Viides rivi
0 - 1 - 1 - 2 - 3 - 5 - 8 - 13 - 21 - 34 - 55 (Tuplavitonen)
Fibonaccin lukujonon ensimmäiset yksitoista lukua järjestyksessä
Joskus Fibonaccin lukujono määritetään alkavan ykkösestä eikä nollasta. Kaksi ensimmäistä numeroa Fibonaccin lukujonossa ovat 0 ja 1 ja seuraavat numerot ovat kahden edellisen numeron summa. Havaitsemme Fibonaccin lukujonon alkavan, kuten Pascalin kolmio.
Suhde kultaiseen leikkaukseen
1/1 = 1,000 Tämä on enemmän näkemisen geometriaa kuin matematiikkaa
3/2 = 1,5000 This is more Phi-Geometry than mathematics
5/3 = 1,666...
8/5 = 1,600
13/8 = 1,625
21/13 = 1,615 Arvo lähenee lopulta tarkaksi
34/21 = 1,619 kultaisen leikkauksen arvoksi
55/34 = 1,617647
89/55 = 1,6181818
...... = ...............
Kultainen leikkaus = 1.61803398874989
Paskalin kolmio 1
Yhdestoista rivi on 1,618 1 1
Lopulta ilmiöt noudattavat kuvatun kaltaista lukujen muodostumista, kukin omalla tavallaan. Pascalin kolmio on kuvio, joka sisältää olevaisen muodostumisen kuvauksen. (397)
63. Kultainen leikkaus tuotteissa
Kaikkialla ympärillämme vaikuttavat erilaiset mittasuhteet, josta esimerkkinä kultainen leikkaus 1,618 tuotteissa. Lisään tuotteita tälle sivulle, joista ensin kaupallinen laskin HP 12 C. Tuotteet sisältävät näkemisen geometriaa, jota ei tarvitse laskea. (821)

Hewlet Packardin 12C kaupallinen laskin sisältää suhteen 1,6125
Mitat (W x D x H)
8.0 x 1.52 x 12.9 cm
12,9 / 8,0 = 1,6125
64. Teräksen ominaispaino
64.1 Ympyrä ja ellipsi

Yksikköympyrän (1) pinta-ala määrittää teräksen ominaispainon. Ympyrän sisään piirretyt kuviot kultaisen leikkauksen suhteessa, määrittävät teräksen mekaaniset ominaisuudet.
64.2 Teräksen yksikköympyrä ja alumii
Laskennan materiaali on teräs. Alkuräjähdyksen yhteydessä syntynyt alkumetalli, sisältäen laskennan perustan.
Teräksen yksikköympyrä, halkaisija ja pituus yksi yksikköä
a) raudan ominaispaino on 7,87 g/cm3.
b) teräs on rautaa, josta on poistettu hiiltä. Hiiltä on muutama prosentti, jolloin ominaispainon arvo 7,87 g/cm3 on toimiva.
Teräksen ominaispaino ja yksikköympyrän pinta-ala ovat määritettäviä kertoimen 1,618 avulla luvusta 1.
6,181 x 1,618 = 10 = 0,6181 x 1,618 = 1
Yksiköillä laskennassa ei ole merkitystä, niiden ollessa ihmisten keksimiä. Tässä tapauksessa ohjelma laski painon grammoina, jolloin ajatellaan luvut arvoiksi 0,6181 ja 1. Tämä on samalla hyvä harjoitus arvoihin. Laskettavan ei tarvitse olla terästä. Laskemme alumiinisen levypalan painon teräksen ominaispainon perusteella. Alumiinin ominaispaino on 2,7 g/cm3.
1,618 / 0,618 x 1,034 = 2,70
Gravitaation 9,82 m/s2 kautta
1,618 /(0,618 x 9,82) x 1,034 = 0,275
Käymme läpi koko matemaattisen paletin, alkaen teräksen palasta, kuten kuvassa ja lopetamme lopputuotteen arvojen muodostukseen. Tämä vaatii ainoastaan malttia ja ajattelutavan yksinkertaistamista. Kuinka välttämätöntä on laskea alumiinin paino esitetyllä tavalla, on toinen tarina. (209)
65. Teräksen lujuus näkemisen geometriana
Platonin mukaan, kuva todellisuudesta muodostui todellisista esineistä, jotka muodostivat varjoja luolan takaseinään. Platonin esimerkissä vanki pääsi luolasta vapauteen, mutta joutui palaamaan takaisin luolaan. Aikaisemmin varjoja nähnyt vanki, kertoi nyt todellisista varjojen takana olevista esineistä. Lopputuloksena, muut vangit halusivat mieluummin tappaa tämän vangin, kuin muuttaa käsitystään todellisuudesta. Nämä muut eivät kenties poikkea meistä, mikäli piirtymättömät varjot näkymättömästä eivät ole tiedossamme. Tieto antaa mahdollisuuden nähdä sellaista, joka ilman tietoa ei ole mahdollista. Sallikaa minun esittää ajatusta enemmän.
1 - 1,12 - 1,25
Se, mitä meillä on paljon, on maapallon teräspitoinen maaperä. Normaalin rakenneteräksen kovuus lujuuslaskentaan on HB 112, keskiarvo vaihteluvälistä HB 100 - 125. Pyöreä ympyrä halkaisijaltaan 112 (*yksiköt ovat teidän), sisältää mittakaavan, teräksen S235 kovuudesta. Jokainen osaa piirtää ympyrän halkaisijaltaan 112 yksikköä, jolloin kaksiulotteinen ympyrä esittää paperilla kovuuden. Ympyrä muodostaa pinta-alan 9852 neliöyksikkömittaa eli toisin sanoin painovoiman 9,82 yksikköä/s2. Tekemällä ympyrästä kolmeulotteisen pallon, sillä voi määrittää teräksen kovuuden. Kuulan painaminen teräksen pintaan, on käytössä oleva menetelmä kovuuden määrittämiseksi.
Alla on kuvio, josta voi jatkaa pitkälle lujuuden määrittämiseksi. Seinälle piirtymättömästä varjosta, näkymättömästä ilmiöstä nimeltään lujuus. Samalla tavalla kuin näkyvällä on näkyvä varjo, on näkymättömällä laskennallinen näkymätön varjo.
*Yksiköt ovat ihmisen keksimiä, kuten mm, tuuma, valovuosi jne. (905)
65.1 Teräksen kovuuden kultainen leikkaus
Jaettaessa ympyrän pinta-ala suuremman ellipsin pinta-alalla, pinta-alat jakaantuvat kultaisen leikkauksen suhteessa 1:1,618. Ellipsin pikkuakselin pituus on kultaisen leikkauksen 1,618 suhteessa ympyrän halkaisijaan. Jaettaessa suuremman ellipsin pinta-ala pienemmän ellipsin pinta-alalla, sisältyy myös tähän kultaisen leikkauksen suhde 1,618.
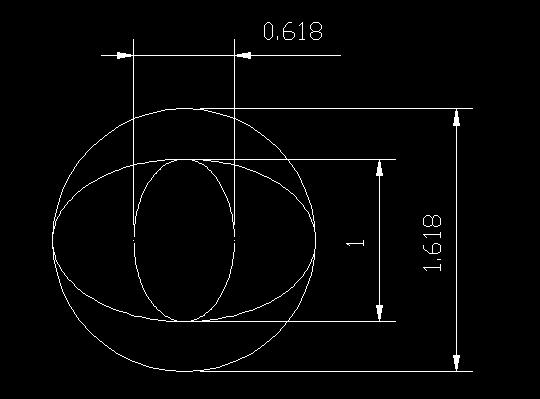
Piirrettäessä ellipsi ellipsin sisälle 1,618 suhteessa, pinta-ala on 1:2,618 edellisestä ellipsistä.
1 + 1,618 = 2,1618 1.618 x 1.618 = 2.618
Ympyrän pinta-ala on 2,0561 yksikköä
Suuremman ellipsin pinta-ala on 1,2708 yksikköä => 2,0561 / 1,2708 = 1,618
Pienemmän ellipsin pinta-ala on 0,4854 yksikköä => 1,2708 / 0,4854 = 2,618
Ympyrä eli pyöreä muoto on materiaalin kovuus, ellipsit lujuutena.
Miksi näin. Selitän sen lujuuslaskennan kautta.
Kultainen leikkaus liittyy koneiden rakennuksen yleisimpään materiaaliin, teräkseen. Kuitenkaan, emme huomaa kultaista leikkausta, valitessa teräslaatua kohteeseen tai tarkastellessa terästen lujuuksia. Teräksen vetolujuus on verrannollinen kovuuteen, siten että vetomurtolujuuteen 100 kN/cm2 saakka hiiliteräksen vetomurtolujuus on 36 % ja seosteräksen 34 % Brinell-kovuudesta. Prosentuaalinen osuus on havaittu, mutta liittymistä kultaiseen leikkaukseen ei.
Suhde φ (1,618). Hiili- ja seosteräksien vetomurtolujuus saadaan varsin tarkasti jakamalla teräksen HB-kovuus luvulla 1,618. => HB 112 / 1,618 = 69,221 => σM = 112 - 69,221 = 42,8 kN/cm2. Arvo 42,8 kN/cm2 vastaa S235 terästälaatua, jonka taattu vetomurtolujuus on vähintään 37 kN/cm2. (377)
HB = Brinell kovuus σM = Vetomurtolujuus
Rakenneteräs S235 HB 100...125
65.2 Taipuman varjo
Kuormitetusta kannattimesta, voi etukäteen laskea taipuman, jännitykset jne., jolloin laskimessa nähtävää laskentatulosta pidetään selviönä. Silti ei ole kauan aikaa, kun tämän kaltainen lujuuden laskenta ei ollut mahdollista. Ajateltaessa asiaa, taipuma on kuormituksen aiheuttama varjo, jonka näkee suuremman kuvan kannatinpalkin alla. Riippuu valon suunnasta, näkeekö taipuman varjon tai ei. Asioiden tarkastelemisessa on samoin, riippuen katsojan näkökulmasta tarkasteltavaan.


Painovoima taivuttaa kannattajaa, jolloin kyse on voimasta. Joskus käytämme voiman yhteydessä nimitystä energia. Energian muunnokset ovat tunnettua, mutta onko taipumalla samaa merkitsevyys muihin asioihin? Varjot ovat yleisesti jotakin, jota ei voi koskettaa. Laskennan tulos on tällainen varjo, taipumaviiva. Näistä varjoista on osittain kyse sivuillani. (786)
66. Lujuus näkemisen geometriana
 Suhdelaskenta esittää matemaattisen selityksen suhdeluvulle 1,618. Tämä esitetään teräksen ja rakenteiden lujuuden näkökulmasta. Tietoa, joka on yhteistä arkkitehdille, insinöörille ja ammatti-ihmisille kaikilla aloilla. Laskennan rajaamatta ketään ulkopuolelle. Suhdelaskenta esittää matemaattisen selityksen suhdeluvulle 1,618. Tämä esitetään teräksen ja rakenteiden lujuuden näkökulmasta. Tietoa, joka on yhteistä arkkitehdille, insinöörille ja ammatti-ihmisille kaikilla aloilla. Laskennan rajaamatta ketään ulkopuolelle.
Tuotesuunnittelija ei ole varsinainen muotoilija, mutta käyttämällä lukusuhdetta 1,618 ja luvun neliöllistä suhdetta 1,25 on suuri mahdollisuus suunnitelman kohteiden olevan miellyttävän näköisiä. Havaitsemme lujuuden rakenteessa noudattavan suhdelukua 1,618.
Esimerkeissä käymme lujuuden laskennan lävitse taivutuksesta väsymiseen. Havaitsemme lujuuden siirtyvän suhteellisena tuotteisiin. Laskemalla oikein yhden tuotteen, muut sarjan tuotteet ovat suurella todennäköisyydellä oikeassa suhteessa. Suhdelaskenta on matemaattinen rakennelma, jolla ei ole loppua.
Näitä tarkasteluja ei tehdä vain tuotteissa, se tehdään kaikissa mahdollisissa ilmiöissä. Rajoite on kokemus tavanomaisen ratkaisun hallitsemisesta. Edellinen, sillä kokemusta tarvitaan laskennan vertaamiseksi perinteiseen laskemistapaan. (299)
66.1 Kultainen kolmio
Kolmiossa kateettien pituudet ovat 1 ja 0,5 yksikköä => hypotenuusa 1,118 yksikköä ja piirin yhteenlaskettu pituus 2,618 yksikköä. Kultainen leikkaus on neliöjuuri 2,618 eli 1,618 x 1,618 = 2,618. Ilmiössä tarkasteltaessa arvon muutosta, tunnettu lähtötieto saa suhteellisen arvon 1. Kun ilmiössä muutos yksiulotteisena on 1,118 (1,12), sen arvoon vaikuttava muutos on 1,4641 kertainen Pascalin kolmion ilmoittamana. Pascalin kolmiossa rivien välinen kerroin 1,1 on käytännön laskentaan 1,12.
Kuvio yllä vasemmalla: 1 / 1,618 = 0,618 kultainen leikkaus 1,618
Kuvio alla vasemmalla: 1 - 1,12 - 1,25 suhdelukujono
kuvio alla oikealla: 2 x 0,5 + 0,618 kultainen leikkaus 1,618
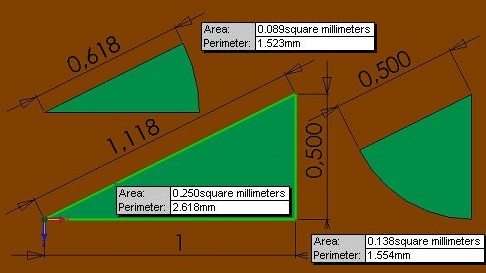
0,618 + 0,500 = 1,118
0,618 / 0,500 = 1,236
1 + (2 x 0,118) = 1,236
1 / 1,618 = 0,618
0,138 / 0,089 = 1,55
1,2362 = 1,527
1,618 x 1,618 = 2,618
1 + 1,618 = 2,618
 Kaksitukisen kannattajan jänneväli kasvaa 1,1(18) kertaiseksi alkuperäisestä pituudesta => taipuma kasvaa 1,46 kertaiseksi. Kaksitukisen kannattajan jänneväli kasvaa 1,1(18) kertaiseksi alkuperäisestä pituudesta => taipuma kasvaa 1,46 kertaiseksi.
Laskemme jotakin, joka on kokonaisuus ja jotakin, joka ei ole.
Kokonaisuus on kolmio ja sen pinta-ala 0,25 yksikköä eli suhdelukujonon kerroin 1,25.
Arvo (1,118), joka ei ole kokonaisuus, ovat yhdessä kaksi sektorin arvoa (0,618 + 0,5 = 1,118. Yksikköjä ei ole, sillä laskemme maailmankaikkeuden laskentaa.
Nähtävän lisäksi on olemassa näkymätön maailman kaikkeuden kitka 1,03 (1,25 => 1,03 taulukossa). On hyvä muistaa, ettei kokonaisuus ole desimaaleja.
Sektori 1 + sektori 2 = 0,227
0,089 + 0.138 = 0,227
Kokonaisuus / osakokonaisuudet = 1,1
0,25 / 0,227 = 1,1
Puuttuva pala kokonaisuutta on Pascalin kolmion rivikerroin 1,1
0,1 1
0,2 1 1 1,1 x 1,0 = 1,1
0,4 1 2 1 1,1 x 1,1 = 1,21
0,8 1 3 3 1 1,1 x 1,21 = 1,33
1.6 1 4 6 4 1 1,1 x 1,331 = 1,46
1 6 1 1 6 1 1,1 x 1,4641 = 1,61
Yhteensä = 6,71 ( x 10 -11 )
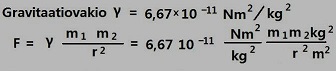
Lopulta Pascalin kolmio muodostaa gravitaatiovakion. Tämä on esimerkki siitä, kuinka geometriset alat näkemisen geometriassa ovat samaa laskutehtävien kanssa. Gravitaatio on toistaiseksi selvittämätön, jossa muutaman desimaalin erolla ei ole merkitystä. (659)
67. Tuotteet näkemisen geometriana
67.1 Nostokorvakkeet 500 - 40 000 kg
Vasemmanpuoleisin nostokorvake on pienin kooltaan. Yhden nostokorvakkeen tiedolla, voi määrittää muiden nostokorvakkeiden painot. Esimerkiksi 40 000 kg nostokorvakkeen paino poikkeaa 5 kg valmistetusta nostokorvakkeen painosta. Painoero pienimmän ja suurimman välillä on noin 200-kertainen. Laskelman tekeminen vie hetken aikaa ja taulukkolaskentaan sijoitettuna ainoastaan muutaman sekunnin.
125 kg x 1,25 x 1,12 = 175 kg on viimeinen rivi laskennassa 40 000 kg nostokorvakkeelle.
Painon muodostumisesta tuotteessa, tulee ymmärtää suhteellisuus eri ulotteisuuksissa. Laskenta esittää myöhemmin kuvan nostokorvakkeiden painon määrittämisen. Paraabeli käyrän muodostumisesta on myös näkemisen geometriaa. (80)
68. Fysiologia näkemisen geometriana
68.1 Lyhyet juoksumatkat Pascalin kolmiossa
Pascalin kolmio näkemisen geometriana
Pascalin kolmio Juoksumatkat Pituudet
1 100 100 m
1 1 100 100 200 m
1 2 1 100 200 100 400 m
1 3 3 1 100 300 300 100 800 m
1 4 6 4 1 100 400 600 400 100 1600 m
Kheops pyramidi

10. Pythagoraan viisikulmio
11. Numero viisi suhdelaskennassa.
Ajattelette, ettei pyramidilla ole tekemistä juoksemisen kanssa, eivätkä eqyptiläiset tuohon aikaan tunnetusti juosseet kilpaa. Ei tarvitsekaan, sillä ilmiöt sisältyvät pyramidimaiseen kuvioon. Tiede jostakin syystä ei halua tätä ymmärtää. Näette kaiketi pyramidin samankaltaisuuden Pascalin kolmioon ja siitä tässä yhteydessä johdettuihin lyhyisiin ratamatkoihin. Tämä havainto riittää hyvin aluksi.
1600 m juoksu on nykyään 1500 m
Pisin juoksumatka - lyhin juoksumatka => 1600 m - 100 m = 1500 m
Pascalin kolmio määrittää ratajuoksun viisi lyhyintä juoksumatkaa eli viisi suhteellista matkaa ilmiöllisessä avaruudessa. Pascalin kolmio on kaksiulotteinen kuvio, jota kolmeulotteisuudessa vastaa pyramidi.
29.9.2015*20:30 (28 - 286)
www.karikolehmainen.com
epcalculation@gmail.com
|