Piin arvo näkemisen geometriana
 Arkhimedes kehitti menetelmän, jolla piin arvon saattoi laskea mielivaltaisen tarkasti. Tämä tapahtui laskemalla ympyrän sisään jäävän säännöllisen n-kulmion kehästä minimiarvo, ympyrän sisäänsä jättävästä n-kulmion kehästä maksimiarvo ja n:ää kasvattamalla arvot lähenivät toisiaan. Arkhimedes kehitti menetelmän, jolla piin arvon saattoi laskea mielivaltaisen tarkasti. Tämä tapahtui laskemalla ympyrän sisään jäävän säännöllisen n-kulmion kehästä minimiarvo, ympyrän sisäänsä jättävästä n-kulmion kehästä maksimiarvo ja n:ää kasvattamalla arvot lähenivät toisiaan.
Archimedes developed a method which could calculate the value of the Pi, having an arbitrary accuracy. This was done by calculating a regular n-gon periphery inside a circle and its minimum value, then submitting the n-gon periphery outside the circle. By increasing the values of the n the values come closer.
Arkhimedes osoitti ympyrän kehän ja halkaisijan pituuksien suhteen (pii) olevan 3,1408 - 3,1429 välillä.
Domenico Fetti Arkhimedes (1620)
Raamattu tunsi piille likiarvon 3 ja Mesopotamiassa tunnettiin likiarvo 3 1/8 (3,125) 2000 vuotta ennen ajanlaskun alkua. Piin arvo on tänä päivänä 3,14159.
Archimedes showed that the circle perimeter and the length of the diameter had the ratio of 3.1408 to 3.1429. The Bible knew the approximate value 3 of Pi, and in Mesopotamia was known as an approximation of 3 1/8 (3.125) 2000 BC. Today, the value of Pi is 3.14159.
Mielenkiintoiseksi piin arvon määrittämisen tekee seikka, että se on määritetty graafisesti ympyrän ja sen sisään jäävän säännöllisen n-kulmion avulla. Samaa tarkoittavassa suhdelaskennassa arvoja voidaan määrittää vastaavalla tavalla graafisesti. Voi sanoa Arkhimedeen ratkaisseen piin arvon näkemisen geometriana.
It is interesting that the determination of the value of Pi, was determined by a regular n-gon periphery inside and outside a circle. Equivalent Proportional Calculation has the same idea that the values can be determined graphically in the same way. It can say Archimedes solved the geometry of the value of Pi by way of Visual Geometry
Menettely piin määrittämiseksi tapahtui laskemalla monikulmion jänteiden pituudet ja suhteuttamalla tämän ympyrän halkaisijan mittaan. Mitä suuremman määrän n-kulmio sisälsi särmän muodostavia jänteitä, sitä lähempänä piin arvo oli. Toisaalta ongelmaksi tulee mittaamiseen käytettävien välineiden tarkkuus, joista on vähän mainintoja.
The determination procedure of Pi was by adding all polygon spans lengths and taking the ratio of the diameter of the circle. The higher the amount of n-gon spans, the closer the value of Pi. On the other hand there is a problem of measuring equipment accuracy of which is a little mention.
Teoriaa ei sovellettu käytäntöön, eikä laskentaa suoritettu käytännön mukaan toimien. Määritettäessä piin arvo tänään, toimimme toisin. Piirtäisimme harpilla pyöreän muodon, jota vieritämme tasaisella alustalla. Tämän jälkeen mittaisimme kuljetun matkan ja suhteuttaisimme matkan kappaleen halkaisijaan. Tekikö Arkhimedes näin varmistaen tuloksen? Eräiden asioiden yhteydessä on havaittavissa, ettei teorian mukaista mallia koskaan valmistettu varmistamaan teoriaa.
The theory was not applied in practice, rather than the calculation performed according to the practical activities. When determining Pi value today, we should have a different approach. We draw a round shape, which we turn on a flat surface. After the measured distance of traveled length, we take the proportion of the diameter. Did Archimedes thus ensuring the value of Pi? Some things can be observed in connection with the theory, the model was never made to ensure the theory.
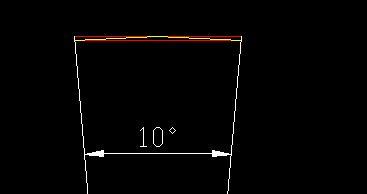
Esimerkki
Nykyaikaisessa piirtämisohjelmassa piirretty ympyrä on halkaisijaltaan 10 mm. Jaamme ympyrän 36 lohkoon, tämän tarkoittaessa lohko on 360 astetta / 36 = 10 astetta. Ohjelmasta saamme tarkan arvon jänteille 0,8716 ja 0,8749 mm ja voimme laskea ympyrän kehän pituuden, kuten Arkhimedes sen aikanaan määritti periaatteessa harpillaan.
36 x (0,8716 + 0,8749) / 2 = 31,437 mm => Pii 3,1437
An Example
We have a modern drawing program and a circle diameter of 10 mm. The circle has been divided to 36 sectors and this means 360 degrees / 36 = 10 degrees. The program gives us the lengths of the spans 0,8716 and 0.8749 mm and we can calculate the perimeter of the circle as Archimedes did in principle with his compass divider.
36 x (0,8716 + 0,8749) / 2 = 31.437 mm => Pi 3.1437
7.7.2012*15:19 (43949 -155)
www.karikolehmainen.com
epcalculation@gmail.com |