Portaiden nousu ja etenemä
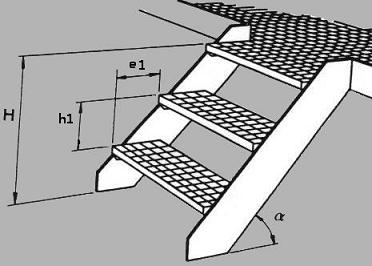 Laskennan lähtökohta on tunnettu tieto tai tiedot, jolloin tuntemattoman saa selville. Portaiden määrityksessä nousu 100 mm ja nousukulma 10 astetta ovat tunnetut tiedot.
Ilman suhdelaskentaa ei voi määrittää taulukon muita arvoja. Tämä tarkoittaa laskennan kykenevän sellaiseen, johon muut laskennat eivät kykene.
Portaiden nousu pystysuunnassa
Portaiden etenemä vaakasuunnassa
Pascalin kolmioon liittyvä kerroin on 1,1. Suhdelaskennan yhteydessä kerroin on välillä 1,1 - 1,12, valittuna keskiarvona usein 1,11. Pascalin kolmio on eräänläinen porraspyramidi kertoimella 1,1(1). Kerroin 1,1(1) liittyy etäisyyden yhteyteen, kuten portaiden nousu. Ilmaistuna tässä yksiköllä mm.
Astetta mm Laskenta
8 90 100 / 1,11 = 90 Käveltävät portaat
10 100 Tunnettu tieto
12,5 11 1,11 x 100 = 111 Kiivettävät portaat
16 123 1,11 x 111 = 123
20 138 1,11 x 123 = 138
25 150 1,11 x 138 = 152
35 170 1,11 x 152 = 169
40 180 1,11 x 169 = 187
50 200 1,11 x 187 = 208
63 230 1,11 x 208 = 230
75 250 -
80 1,11 x 230 = 256
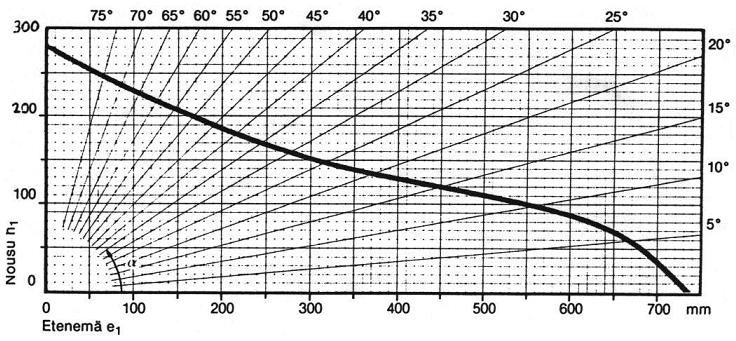
Pascalin kolmion kertoimella 1,1(1) voi laskea porrasaskelman nousun portaissa, josta esimerkki askelmat nousukulmilla 10... 80º. Lähtöarvo on portaiden nousu 100 mm, astekulmalla 10 astetta. Käveltävä kaltevuus 5 astetta taulukossa saadaan jakamalla tunnettu pienin nousun arvo kultaisen leikkauksen kertoimella 1,618 eli 100 mm / 1,618 = 62 mm. Lasketut portaat ovat millimetrien tarkkuudella taulukon arvoon nähden ja arvossa 80 astetta ollaan tarkassa arvossa. Portaiden nousu on alkujaan määritetty kokeellisesti. Kokeellisesti saavutetut tulokset, eivät poikkea laskemalla määritetystä. Mikäli poikkeama havaitaan, voi sanoa sen johtuvan kokeellisesti määritetyistä arvoista enemmän, kuin laskennan virheestä.
Usean standardin voi korvata arvolla ja siihen liittyvällä kertoimella. Lujuuslaskennassa käyrästöjä (ei vain yhtä käyrää, kuten kuvassa) korvataan rivitiedolla, jolloin kaikki käyrät ovat tunnetut. Myös ne käyrät, joita ei ole määritetty.
17.4.2015*08:40 (110 - 1065)
www.karikolehmainen.com
epcalculation@gmail.com |
